数据结构与算法 - 基础：二叉搜索树

摘要

如果使用线性表存放 n 个元素时，时间复杂度是 O(n)。如果使用二分法搜索，可以降低时间复杂度，为 O(logn)，但是添加和删除的平均时间复杂度是 O(n)。

使用二叉搜索树，可以让添加、删除、搜索的最坏时间复杂度优化到 O(logn)。

二叉搜索树，英文为 Binary Search Tree，简称 BST。它是二叉树中的一种，应用的场景也是非常广泛，其他地方也叫做二叉查找树、二叉排序树。主要特点有：

任意一个节点的值都大于它左子树所有节点的值
任意一个节点的值都小于它右子树所有节点的值
它的左右子树也是一棵二叉搜索树

List 1: 二叉搜索树#

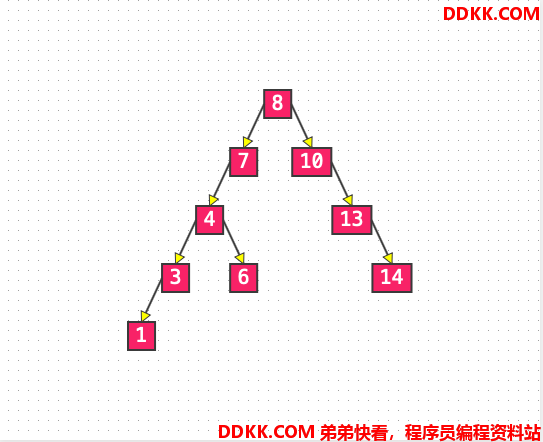
二叉搜索树能够大大提高搜索的效率，但是节点中存储的元素必须具备可比较性，否则搜索效率无从谈起。

可比较性

可以比较大小，比如 int、double。这里也可以自己定义比较规则。

但是 null 是不具有可比较性，也就是元素必须不能为 null。

设计接口

在实现二叉搜索树功能之前，先定义二叉搜索树的接口，对外使用的接口：

1、元素的数量；

int size()

2、是否为空；

boolean isEmpty()

3、清空所有元素；

void clear()

4、添加元素；

void add(E element)

5、删除元素；

void remove(E element)

6、是否包含某元素；

boolean contains(E element)

实现

首先搭建一个类，定义根节点等变量

public class BinarySearchTree<E> implements BinaryTreeInfo {
   
     
  // 记录节点的数量
	int size = 0;
  // 根目录
	Node<E> root;
}

Node 是对节点的定义，感兴趣的，可以找找前几期。

有了size 和 root 就可以快速实现前三个接口：

int size() {
   
     
  return size;
}

boolean isEmpty() {
   
     
  return size == 0;
}

void clear() {
   
     
  root = null;
  size = 0; // size 必须要清空
}

添加元素

添加元素就是创建包含该元素的节点，然后放到合适的位置，比如在原来的二叉搜索树中添加 12 和 5，得到的结果是：

List2: 添加元素 5 和元素 12#

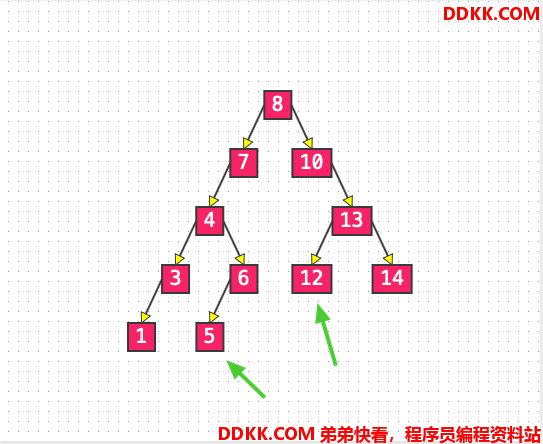
以添加5 来看，5 是怎么跑到 6 的左子树中的：

1、根节点是8（不为null），5和8比较，结果小于8，向8的左子树跑；
2、 8的左子树是7（不为null），5和7比较，结果小于7，向7的左子树跑；
3、 7的左子树是4（不为null），5和4比较，结果大于4，向4的右子树跑；
4、 4的右子树是6（不为null），5和6比较，结果小于6，向6的左子树跑；
5、发现6的左子树是null，确定6是5的父节点；
6、因为5小于6，那么5就放在6的左子树中；

总结出添加的步骤为先找到父节点，然后根据和父节点的比较结果决定放在对应的位置。比较下来，似乎没有说如果元素相等，怎么办？这里简单直接的处理就是覆盖原来的元素，完成。

代码实现：

void add(E element) {
   
     
  // 判断 element 不能为 null。
  elementNotNullCheck(element);
  // 是否是添加到第一个元素
  if (root == null) {
   
     
    root = new Node<E>(element, null);
    size ++;
    return;
  }
  
  // 添加到其他位置
  Node<E> node = root;
  Node<E> parent = null;
  int cmp = 0;
  while (node != null) {
   
     
    parent = node;
    cmp = compare(element, node.element);
    if (cmp > 0) {
   
     
      node = node.right;
    }
    else if (cmp < 0) {
   
     
      node = node.left;
    }
    else {
   
     
      // 元素相等，就直接替换，完成
      node.element = element;
      return;
    }
  }

  // 注意是插入 parent 的 left 或者 right
  Node<E> newNode = new Node<>(element, parent);
  if (cmp > 0) {
   
     
    parent.right = newNode;
  }
  else if (cmp < 0) {
   
     
    parent.left = newNode;
  }
  else {
   
     

  }
}

compare 是自定义的比较方法，感兴趣可以看最后的补充部分。

是否包含某元素

趁热打铁，可以使用 compare 方法可以实现根据元素内容获取节点的方法：

public Node<E> node(E element) {
   
     
  if (element == null) {
   
      return null; }
  Node<E> node = root;
  while (node != null) {
   
     
    int cmp = compare(element, node.element);
    if (cmp > 0) {
   
     
      node = node.right;
    }
    else if (cmp < 0) {
   
     
      node = node.left;
    }
    else {
   
     
      return node;
    }
  }
  return null;
}

那么是否包含某个元素也就可以转换为判断该元素获取到的节点是否为 null：

boolean contains(E element) {
   
     
  return node(element) != null;
}

删除元素

删除元素也是可以转换为删除节点，二叉搜索树删除节点有3种情况要考虑处理：

1、节点是叶子节点；
2、节点是度为1的节点；
3、节点是度为2的节点；

度是什么？

度是节点中子节点的个数，二叉树中每个节点的度最小为 0，最大为 2。

叶子节点就是度为 0 的节点

节点是叶子节点

若删除的节点是叶子节点，处理上比较简单，就是将这个叶子节点设置为 null。这里只需要考虑这个节点是根节点的情况，遇到这个情况就需要将 root = null 处理。

节点是度为 1 的节点

若删除的节点是度为 1 的节点，那么就可以用这个节点的子节点来替代它的位置。当然也要考虑若这个节点是根节点，那么就需要将 root 指向它的子节点。

List3: 删除元素 4 和元素 13#

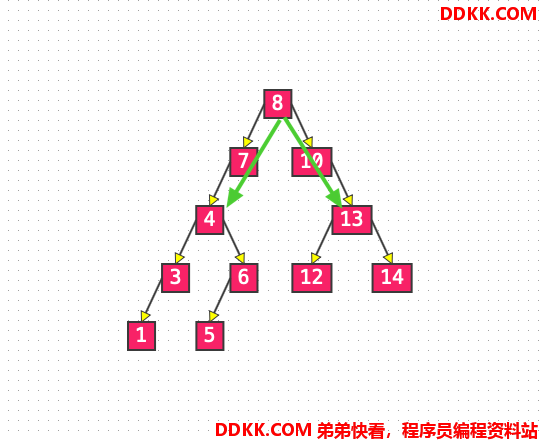
节点的度为 2 的节点

若删除的节点是度为 2 的节点，那么就需要先找到这个节点的前驱或者后继节点，覆盖该节点，然后删除再删除对应的前驱或者后继。（前驱或者后继，详细看最底部补充部分）

这样做是为了保持继续保持节点的左子树都比节点小，节点的右子树都比节点大的性质。

List4: 删除度为 2 的元素 8#

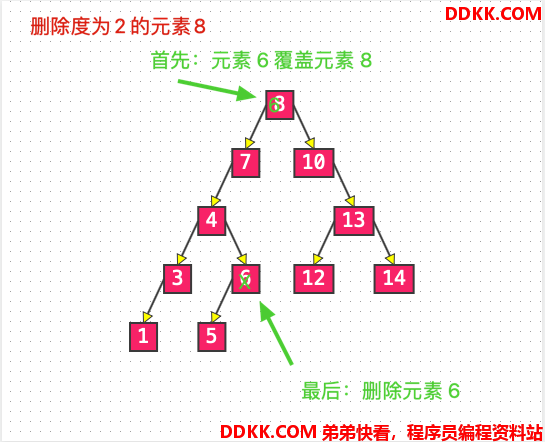
实现

整理梳理完删除节点的三种情况后，可以看到度为 2 的节点是在更换前驱或者后继之后，再次回到了处理度为 0 或者 1 的情况下，接下来的处理，在最后去判断是否是根节点，那么代码实现逻辑上就可以先处理度是 2 的节点，然后处理度为 0 或者 1 的节点，在最后判断节点是否是 root 节点。

void remove(Node<E> node) {
   
     
  if (node == null) {
   
      return; }
  size --;

  // 度为 2 的节点
  if (node.isHaveTowChildren()) {
   
     

    // 找到后继节点
    Node<E> s = successor(node);

    // 后继节点的值赋值给 node
    node.element = s.element;

    // s 节点给 node 节点，为删除 node 节点准备
    node = s;
  }

  // 节点的度非 0 即 1
  Node<E> replaceNode = node.left != null ? node.left : node.right;

  // 度为 1 的节点
  if (replaceNode != null) {
   
     
    replaceNode.parent = node.parent;
    // root 节点
    if (node.parent == null) {
   
     
      root = replaceNode;
    }
    else if (node == node.parent.left) {
   
     
      node.parent.left = replaceNode;
    }
    else {
   
     
      node.parent.right = replaceNode;
    }
  }
  else if (node.parent == null) {
   
      // 度为 0 的节点，且是 root
    root = null;
  }
  else {
   
      // node 是叶子节点，但不是 root
    if (node == node.parent.left) {
   
     
      node.parent.left = null;
    }
    else {
   
     
      node.parent.right = null;
    }
  }
}

补充

compare 方法

这里使用 JAVA 系统中的 Comparator 类，先创建对象，设置 E 类型，保证 E 类型的数据遵守比较协议：

private Comparator<E> comparator;

之后实现比较方法：

private int compare(E e1, E e2) {
   
     
  if (comparator == null) {
   
     
    return ((Comparable<E>)e1).compareTo(e2);
  }
  return comparator.compare(e1, e2);
}

前驱节点和后继节点

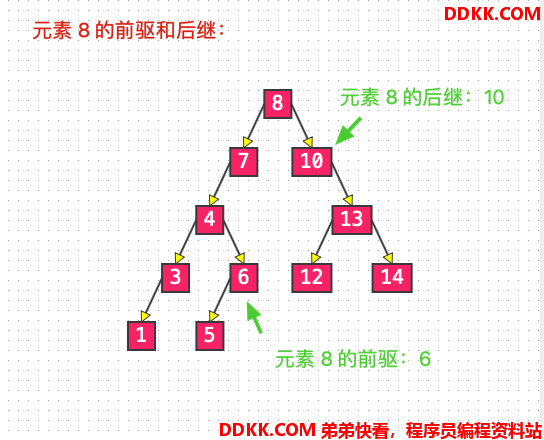
前驱节点是中序遍历时的前一个节点，也是二叉搜索树中，比它小的前一个节点。

即为node.left.right.right...，但是当 node.left == null 时，为 node 的父节点（比如元素 5 的前驱为元素 4）。

后继节点是中序遍历时的后一个节点，也是二叉搜索树中，比它大的后一个节点。

即为node.right.left.left...，但是当 node.right == null 时，为 node 的父节点（比如元素 5 的后继为元素 6）。

List 6: 前驱和后继#

predecessor 获取前驱节点

要留意代码中的终止条件

public Node<E> predecessor(Node<E> node) {
   
     
  if (node == null) return null;

  // 前驱节点在左子树中
  Node<E> p = node.left;
  if (p != null) {
   
     
    while (p.right != null) {
   
     
      p = p.right;
    }
    return p;
  }
  
  while (node.parent != null && node == node.parent.left) {
   
     
    // 前驱节点在父节点中，并 node 在 parent 的右子树中
    node = node.parent;
  }
  // node.parent == null
  // node == node.parent.right
  return node.parent;
}

successor 获取后继节点