简介
哈希表是一种数据结构,它可以提供快速的插入操作和查找操作。哈希表运算得非常快,在计算机程序中,如果需要在一秒种内查找上千条记录,通常使用哈希表 (例如拼写检查器)。哈希表的速度明显比树快,正如前面儿章看到的,树的操作通常需要O(N)的时间级。哈希表不仅速度快,编程实现也相对容易。
哈希表也有一些缺点: 它是基于数组的,数组创建后难于扩展。某些哈希表被基本填满时,性能下降得非常严重,所以程序员必须要清楚表中将要存储多少数据(或者准备好定期地把数据转移到更大的哈希表中,这是个费时的过程)。
Hash表也称散列表,也有直接译作哈希表,Hash表是一种根据关键字值(key - value)而直接进行访问的数据结构。它基于数组,通过把关键字映射到数组的某个下标来加快查找速度,但是又和数组、链表、树等数据结构不同,在这些数据结构中查找某个关键字,通常要遍历整个数据结构,也就是O(N)的时间级,但是对于哈希表来说,只是O(1)的时间级。
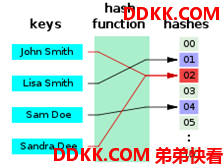
注意,这里有个重要的问题就是如何把关键字转换为数组的下标,这个转换的函数称为哈希函数(也称散列函数),转换的过程称为哈希化。
什么是Hash?
Hash(哈希),又称“散列”。
Hash,就是把任意长度的输入,通过散列算法,变换成固定长度的输出,该输出就是散列值。
这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能
会散列成相同的输出,而不可能从散列值来唯一的确定输入值。
在介绍一些集合时,我们总强调需要重写某个类的 equlas() 方法和 hashCode() 方法,确保唯一性。这里的 hashCode() 表示的是对当前对象的唯一标识。计算 hashCode 的过程就称作 哈希。
为什么要有 Hash
我们通常使用数组或者链表来存储元素,一旦存储的内容数量特别多,需要占用很大的空间,而且在查找某个元素是否存在的过程中,数组和链表都需要挨个循环比较,而通过 哈希 计算,可以大大减少比较次数。
举个栗子:
现在有4 个数 {2,5,9,13},需要查找 13 是否存在。
1.使用数组存储,需要新建个数组 new int[]{2,5,9,13},然后需要写个循环遍历查找:
int[] numbers = new int[]{2,5,9,13};
for (int i = 0; i < numbers.length; i++) {
if (numbers[i] == 13){
System.out.println("find it!");
return;
}
}
这样需要遍历 4 次才能找到,时间复杂度为 O(n)。
2、而假如存储时先使用哈希函数进行计算,这里我随便用个函数:
H[key] = key % 3;
四个数{2,5,9,13} 对应的哈希值为:
H[2] = 2 % 3 = 2;
H[5] = 5 % 3 = 2;
H[9] = 9 % 3 = 0;
H[13] = 13 % 3 = 1;
然后把它们存储到对应的位置。
当要查找 13 时,只要先使用哈希函数计算它的位置,然后去那个位置查看是否存在就好了,本例中只需查找一次,时间复杂度为 O(1)。
因此可以发现
哈希 其实是随机存储的一种优化,先进行分类,然后查找时按照这个对象的分类去找。哈希通过一次计算大幅度缩小查找范围,自然比从全部数据里查找速度要快。
哈希函数
哈希的过程中需要使用哈希函数进行计算。
哈希函数是一种映射关系,根据数据的关键词 key ,通过一定的函数关系,计算出该元素存储位置的函数。
几种常见的哈希函数
直接定址法
- 取关键字或关键字的某个线性函数值为散列地址。
- 即 H(key) = key 或 H(key) = a*key + b,其中a和b为常数。
除留余数法
- 取关键字被某个不大于散列表长度 m 的数 p 求余,得到的作为散列地址。
- 即 H(key) = key % p, p < m。
数字分析法
- 当关键字的位数大于地址的位数,对关键字的各位分布进行分析,选出分布均匀的任意几位作为散列地址。
- 仅适用于所有关键字都已知的情况下,根据实际应用确定要选取的部分,尽量避免发生冲突。
平方取中法
- 先计算出关键字值的平方,然后取平方值中间几位作为散列地址。
- 随机分布的关键字,得到的散列地址也是随机分布的。
折叠法(叠加法)
- 将关键字分为位数相同的几部分,然后取这几部分的叠加和(舍去进位)作为散列地址。
- 用于关键字位数较多,并且关键字中每一位上数字分布大致均匀。
随机数法
- 选择一个随机函数,把关键字的随机函数值作为它的哈希值。
- 通常当关键字的长度不等时用这种方法。
构造哈希函数的方法很多,实际工作中要根据不同的情况选择合适的方法,总的原则是尽可能少的产生冲突。
通常考虑的因素有关键字的长度和分布情况、哈希值的范围等。
如:当关键字是整数类型时就可以用除留余数法;如果关键字是小数类型,选择随机数法会比较好。
哈希冲突的解决
选用哈希函数计算哈希值时,可能不同的 key 会得到相同的结果,一个地址怎么存放多个数据呢?这就是冲突。
常用的主要有两种方法解决冲突:
1.链接法(拉链法)
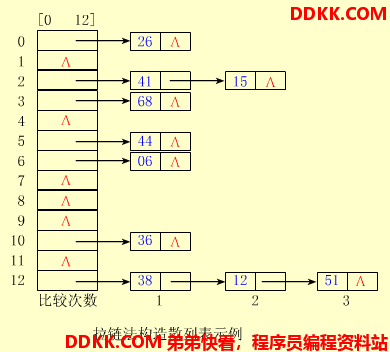
拉链法解决冲突的做法是:
将所有关键字为同义词的结点链接在同一个单链表中。
若选定的散列表长度为 m,则可将散列表定义为一个由 m 个头指针组成的指针数组 T[0..m-1] 。
凡是散列地址为 i 的结点,均插入到以 T[i] 为头指针的单链表中。
T中各分量的初值均应为空指针。
在拉链法中,装填因子 α 可以大于 1,但一般均取 α ≤ 1。
2.开放定址法
用开放定址法解决冲突的做法是:
用开放定址法解决冲突的做法是:当冲突发生时,使用某种探测技术在散列表中形成一个探测序列。沿此序列逐个单元地查找,直到找到给定的关键字,或者碰到一个开放的地址(即该地址单元为空)为止(若要插入,在探查到开放的地址,则可将待插入的新结点存人该地址单元)。查找时探测到开放的地址则表明表中无待查的关键字,即查找失败。
简单的说:当冲突发生时,使用某种探查(亦称探测)技术在散列表中寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到。
按照形成探查序列的方法不同,可将开放定址法区分为线性探查法、二次探查法、双重散列法等。
a.线性探查法
hi=(h(key)+i) % m ,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+1],…,直到 T[m-1],此后又循环到 T[0],T[1],…,直到探查到 有空余地址 或者到 T[d-1]为止。
b.二次探查法
hi=(h(key)+i*i) % m,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+1^2],T[d+2^2],T[d+3^2],…,等,直到探查到 有空余地址 或者到 T[d-1]为止。
缺点是无法探查到整个散列空间。
c.双重散列法
hi=(h(key)+i*h1(key)) % m,0 ≤ i ≤ m-1
基本思想是:
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+h1(d)], T[d + 2*h1(d)],…,等。
该方法使用了两个散列函数 h(key) 和 h1(key),故也称为双散列函数探查法。
定义h1(key) 的方法较多,但无论采用什么方法定义,都必须使 h1(key) 的值和 m 互素,才能使发生冲突的同义词地址均匀地分布在整个表中,否则可能造成同义词地址的循环计算。
该方法是开放定址法中最好的方法之一。