题目地址：https://leetcode-cn.com/problems/as-far-from-land-as-possible/
题目描述
你现在手里有一份大小为 N x N 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的。
我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1|。
如果网格上只有陆地或者海洋，请返回 -1。
示例1：
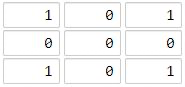
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。
示例2：
输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。
提示：
1、 1<=grid.length==grid[0].length<=100；
2、 grid[i][j]不是0就是1；
题目大意
找出哪片海洋距离所有的陆地距离最远。
解题方法
这个题想考察什么？
虽然题目千变万化，但是考察点永远是那几个。本题给出了一个场景：求所有海洋点到离它最近的陆地点的距离的最大值。那么我们求出每一个海洋点到其最近陆地点的最短距离，在这些最短距离中找最大值不就好了么？
在向下阅读之前，一定要确保你理解了题意。其中曼哈顿距离就是只能沿着横、竖到达另外一个点走的步数。
题目给出的两个示例：
example 1：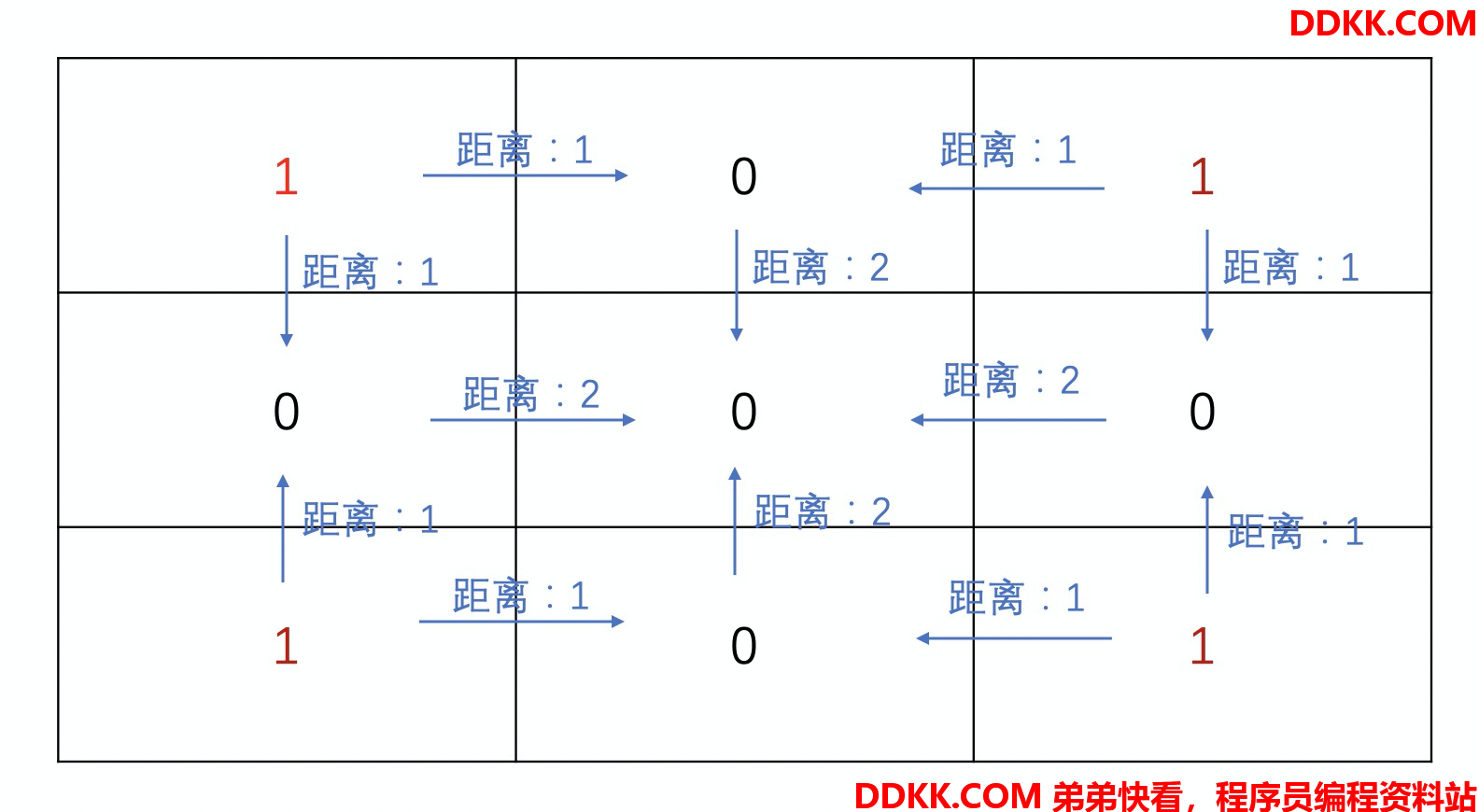 
题目所求是中间那个0，距离所有1的距离最大为2.
example 2：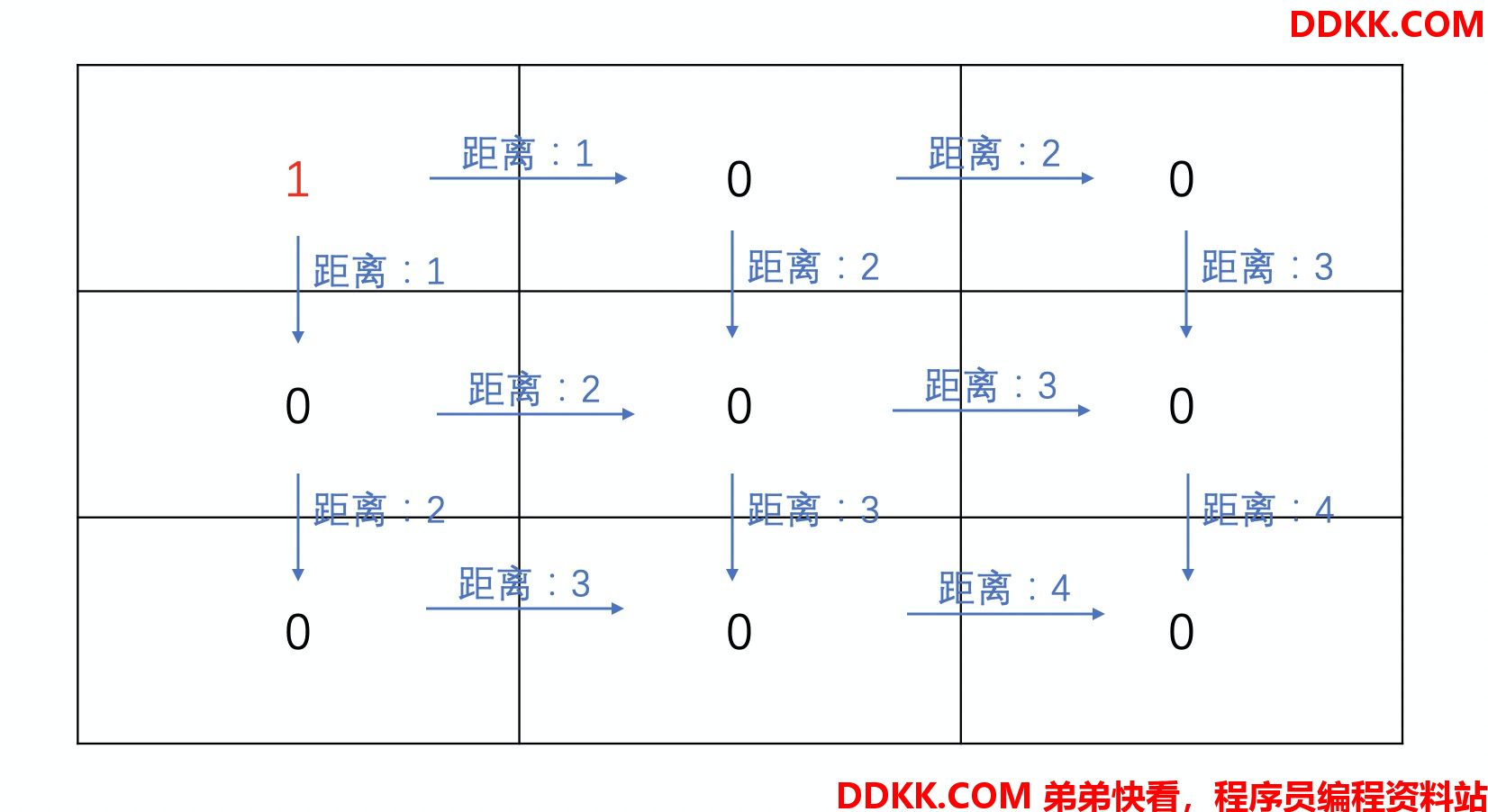 
题目所求是有下角那个0，距离所有1的距离最大为4.
在一个图中，能从一个点出发求这种最短距离的方法很容易想到就是BFS，BFS的名称是广度优先遍历，即把周围这一圈搜索完成之后，再搜索下一圈，是慢慢扩大搜索范围的。
图左边是BFS，按照层进行搜索；图右边是DFS，先一路走到底，然后再回头搜索。
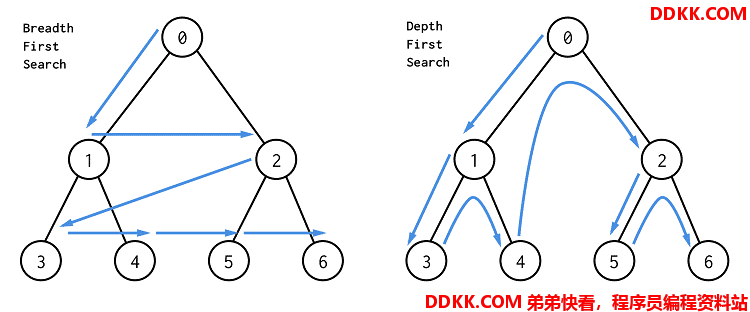
题目给出了多个陆地，要找出每个海洋点A到陆地B的最近曼哈顿距离。由于A到B的距离和B到A的距离一样的，所以其实我们可以换个思维：找出每个陆地B到所有海洋点A的距离，对每个海洋点A取最小距离就好了。
因此，题目可以抽象成：多个起始点的BFS。恭喜你已经解决了一半问题。
剩下的任务就是套模板！
我在博客中已经总结了所有常见的算法模板，【LeetCode】代码模板，刷题必会open in new window，直接拿来用！
BFS使用队列，把每个还没有搜索到的点一次放入队列，然后再弹出队列的头部元素当做当前遍历点。
如果不需要确定当前遍历到了哪一层，BFS模板如下。
while queue 不空：
cur = queue.pop()
for 节点 in cur的所有相邻节点：
if 该节点有效且未访问过：
queue.push(该节点)
1 2 3 4 5
如果要确定当前遍历到了哪一层，BFS模板如下。这里增加了level表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size表示在开始遍历新的一层时，队列中有多少个元素，即有多少个点需要向前走一步。
level = 0
while queue 不空：
size = queue.size()
while (size --) {
cur = queue.pop()
for 节点 in cur的所有相邻节点：
if 该节点有效且未被访问过：
queue.push(该节点)
}
level ++;
1 2 3 4 5 6 7 8 9 10
上面两个是通用模板，在任何题目中都可以用，是要记住的！
上面说了这个题是多个起始点的BFS，不要害怕，就是需要先遍历一遍矩阵，把所有陆地先放进队列中，然后再利用模板二。
至此，把上面的思路套进模板，题目就能解决了。
在C++中可以使用queue作为队列。我下面使用的是deque双端队列，但是只当做单端的队列来用。
C++代码如下，如果看不懂C++也不要紧，注释很详细。
class Solution {
public:
int maxDistance(vector<vector<int>>& grid) {
const int M = grid.size();
const int N = grid[0].size();
// 使用deque作为队列
deque<pair<int, int>> deq;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (grid[i][j] == 1) {
// 将所有陆地都放入队列中
deq.push_back({i, j});
}
}
}
// 如果没有陆地或者海洋，返回-1
if (deq.size() == 0 || deq.size() == M * N) {
return -1;
}
// 由于BFS的第一层遍历是从陆地开始，因此遍历完第一层之后distance应该是0
int distance = -1;
// 对队列的元素进行遍历
while (deq.size() != 0) {
// 新遍历了一层
distance ++;
// 当前层的元素有多少，在该轮中一次性遍历完当前层
int size = deq.size();
while (size --) {
// BFS遍历的当前元素永远是队列的开头元素
auto cur = deq.front(); deq.pop_front();
// 对当前元素的各个方向进行搜索
for (auto& d : directions) {
int x = cur.first + d[0];
int y = cur.second + d[1];
// 如果搜索到的新坐标超出范围/陆地/已经遍历过，则不搜索了
if (x < 0 || x >= M || y < 0 || y >= N ||
grid[x][y] != 0) {
continue;
}
// 把grid中搜索过的元素设置为2
grid[x][y] = 2;
// 放入队列中
deq.push_back({x, y});
}
}
}
// 最终走了多少层才把海洋遍历完
return distance;
}
private:
vector<vector<int>> directions = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
DDKK.COM 弟弟快看-教程，程序员编程资料站，版权归原作者所有
本文经作者：负雪明烛 授权发布，任何组织或个人未经作者授权不得转发