题目地址:https://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/description/
题目描述
Wehave two integer sequences A and B of the same non-zero length.
Weare allowed to swap elements A[i] and B[i]. Note that both elements are in the same index position in their respective sequences.
Atthe end of some number of swaps, A and B are both strictly increasing. (A sequence is strictly increasing if and only if A[0] < A[1] < A[2] < ... < A[A.length - 1].)
Given A and B, return the minimum number of swaps to make both sequences strictly increasing. It is guaranteed that the given input always makes it possible.
Example:
Input: A = [1,3,5,4], B = [1,2,3,7]
Output: 1
Explanation:
Swap A[3] and B[3]. Then the sequences are:
A = [1, 3, 5, 7] and B = [1, 2, 3, 4]
which are both strictly increasing.
Note:
- A, B are arrays with the same length, and that length will be in the range [1, 1000].
- A[i], B[i] are integer values in the range [0, 2000].
题目大意
一个字符串中有0有1,问最少翻转多少个字符能够使得这个字符串编程一个单调递增的字符串。
解题方法
动态规划
这个题和周赛926. Flip String to Monotone Increasingopen in new window基本一模一样,如果我早点把这个题搞明白的话,周赛的926应该也能做出来了。926题我写的非常的详细,是我写的最认真的一次,强烈建议看下926题的动态规划部分。
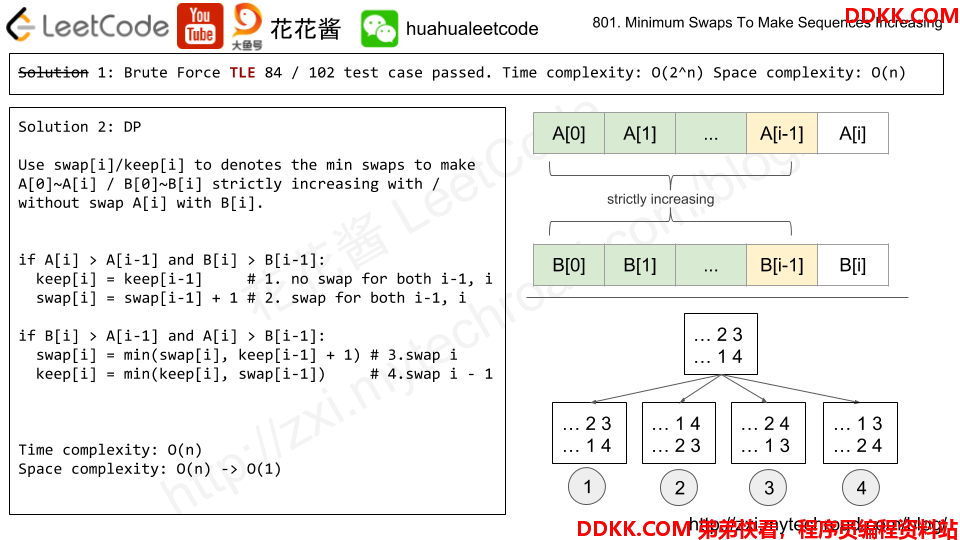
我是看了画画酱的讲义的,如下图。这个题也是需要做交换,可以定义两个数组keep和swap,这两个数组的含义是我们交换或者不交换第i个位置使得两个数组都保持严格的单调递增需要进行的交换数量。
那么,当A[i] > A[i - 1] and B[i] > B[i - 1]时,我们可以不交换当前的数字,这个时候前面的数字也不能交换;也可以交换当前的数字,同时需要把前面的数字也进行交换。即,这种情况下,前面的位置和现在的位置做的是同样的交换。
在做了上面的操作之后,我们得到的仍然是有序的部分,但是没有结束,因为我们可能还会出现A[i] > B[i - 1] and B[i] > A[i - 1]这种交叉的情况。这个时候考虑前面的位置和现在的位置做相反的交换。
当A[i] > B[i - 1] and B[i] > A[i - 1]时,我们如果不交换当前的数字,同时对前面的位置强制交换,判断交换后的次数是不是比当前的交换次数少;如果我们交换这个位置,同时强制前面的数字不交换,那么当前的交换次数应该是前面不交换的次数+1和当前交换次数的最小值。
上面两种判断并不是if-else的关系,因为,这两种情况同时存在。我们通过这两种情况,考虑了4种情况:当前位置换、不换与前面的位置换、不换的组合。注意第二个判断里面求最小值是相对于自身做比较的,因为我们不一定需要对前面的位置进行操作。
另外,需要注意的是,一般情况的dp初始化都是0或者1,但是这个题需要求最小值,其实已经提醒我们不是0或者1.实际上,需要使用无穷大表示初始情况下,还没有做翻转操作时交换次数应该是无穷多。而不是0表示初始情况下不用交换就能到达有序。
时间复杂度是O(N),空间复杂度是O(N).
class Solution(object):
def minSwap(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: int
"""
N = len(A)
keep = [float('inf')] * N
swap = [float('inf')] * N
keep[0] = 0
swap[0] = 1
for i in range(1, N):
if A[i] > A[i - 1] and B[i] > B[i - 1]:
keep[i] = keep[i - 1]
swap[i] = swap[i - 1] + 1
if A[i] > B[i - 1] and B[i] > A[i - 1]:
keep[i] = min(keep[i], swap[i - 1])
swap[i] = min(swap[i], keep[i - 1] + 1)
return min(keep[N - 1], swap[N - 1])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
这个题如果改成和926题一样的二维数组的dp的话,应该这么写,其实和上面的做法没有任何区别。
class Solution(object):
def minSwap(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: int
"""
N = len(A)
dp = [[float('inf'), float('inf')] for _ in range(N)]
dp[0][0] = 0
dp[0][1] = 1
for i in range(1, N):
if A[i] > A[i - 1] and B[i] > B[i - 1]:
dp[i][0] = dp[i - 1][0]
dp[i][1] = dp[i - 1][1] + 1
if A[i] > B[i - 1] and B[i] > A[i - 1]:
dp[i][0] = min(dp[i][0], dp[i - 1][1])
dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1)
return min(dp[N - 1][0], dp[N - 1][1])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
显然,上面的做法中,每次dp转移操作只和前面的一个状态有关,所以,可以优化空间复杂度到O(1)。对于每次
代码如下:
class Solution(object):
def minSwap(self, A, B):
"""
:type A: List[int]
:type B: List[int]
:rtype: int
"""
N = len(A)
keep, swap = 0, 1
for i in range(1, N):
curswap, curkeep = float('inf'), float('inf')
if A[i] > A[i - 1] and B[i] > B[i - 1]:
curkeep, curswap = keep, swap + 1
if A[i] > B[i - 1] and B[i] > A[i - 1]:
curkeep, curswap = min(curkeep, swap), min(curswap, keep + 1)
keep, swap = curkeep, curswap
return min(keep, swap)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
参考资料
https://leetcode.com/problems/flip-string-to-monotone-increasing/discuss/183859/Java-DP-using-O(N)-time-and-O(1)-space
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发