题目地址:https://leetcode.com/problems/maximum-average-subarray-i/description/open in new window
题目描述
Given an array consisting of n integers, find the contiguous subarray of given length k that has the maximum average value. And you need to output the maximum average value.
Example 1:
Input: [1,12,-5,-6,50,3], k = 4
Output: 12.75
Explanation: Maximum average is (12-5-6+50)/4 = 51/4 = 12.75
Note:
1、 1<=k<=n<=30,000.;
2、 Elementsofthegivenarraywillbeintherange[-10,000,10,000].;
题目大意
求给定数组中长度为k的切片的最大平均值。
解题方法
首先需要区分两个概念:子串(子数组)和子序列。
这两个名词经常在题目中出现,非常有必要加以区分。
子串sub-string(子数组 sub-array)是连续的,而子序列 subsequence 可以不连续。
方法一:preSum
今天题目让求最大平均数,由于 k 是不变的,因此可以先求区间的最大和,然后再除以 k。
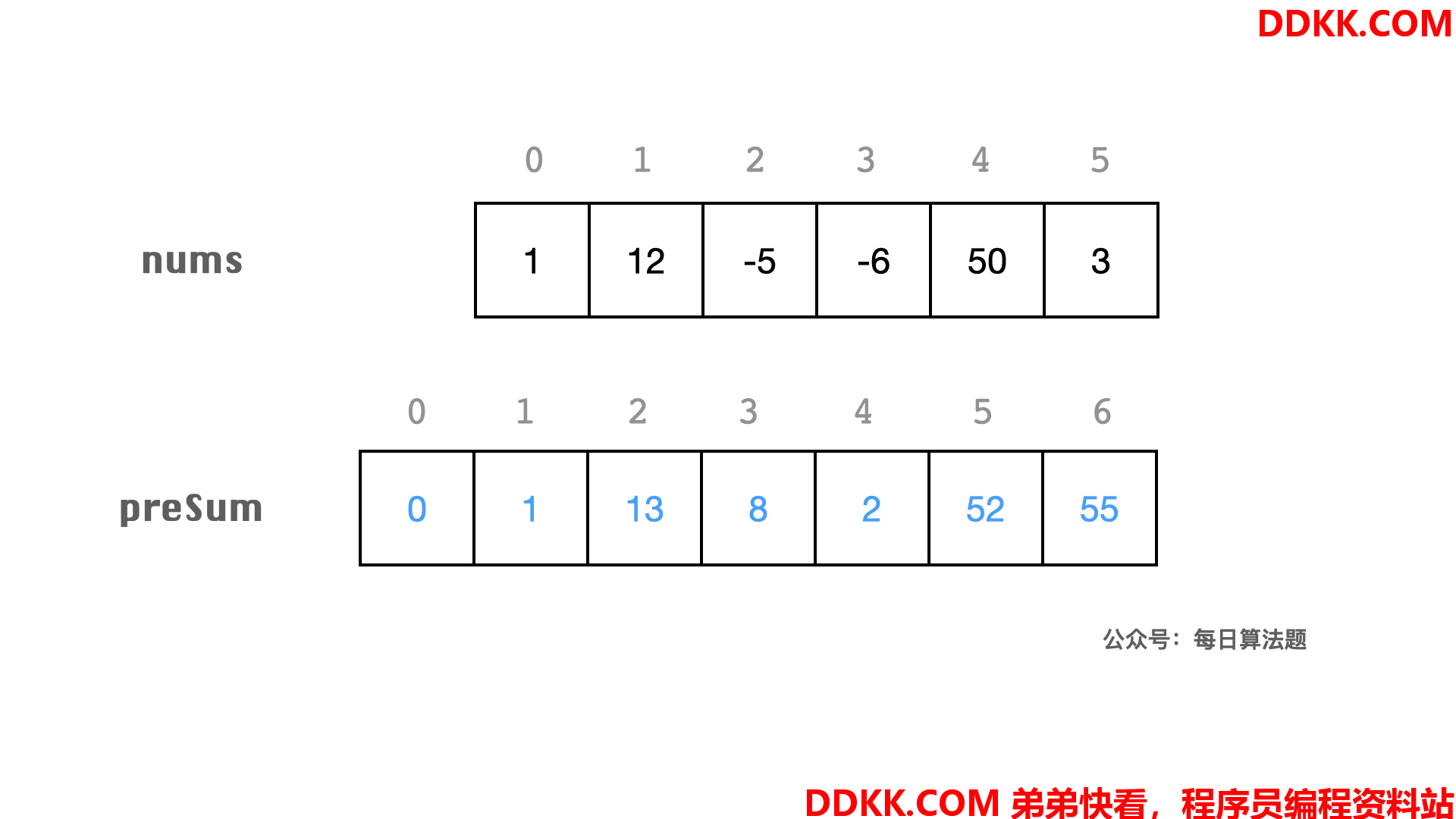
上周我在题解中已经说过,求区间的和可以用 preSum。preSum 方法还能快速计算指定区间段 i ~ j 的元素之和。它的计算方法是从左向右遍历数组,当遍历到数组的 i 位置时,preSum表示 i 位置左边的元素之和。
假设数组长度为 N,我们定义一个长度为 N+1 的 preSum 数组,preSum[i] 表示该元素左边所有元素之和(不包含当前元素) 。然后遍历一次数组,累加区间 [0, i) 范围内的元素,可以得到 preSum 数组。代码如下:
N = len(nums)
preSum = range(N + 1)
for i in range(N):
preSum[i + 1] = preSum[i] + nums[i]
print(preSum)
1 2 3 4 5
利用preSum 数组,可以在 O(1) 的时间内快速求出 nums 任意区间 [i, j] (两端都包含) 的各元素之和。
sum(i, j) = preSum[i + 1] - preSum[j]
对于本题,可以先遍历一次,求数组每个位置的 preSum,然后再遍历一次,求长度为 k 的每个区间的最大和。最终除以 k 得到最大平均数。
使用Python2 写的代码如下。
class Solution(object):
def findMaxAverage(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: float
"""
N = len(nums)
preSum = range(N + 1)
for i in range(N):
preSum[i + 1] = preSum[i] + nums[i]
largest = float("-inf")
for i in range(k - 1, N):
largest = max(preSum[i + 1] - preSum[i + 1 - k], res)
return largest / float(k)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
方法二:滑动窗口
题目也可以抽象成长度固定为 k 的滑动窗口。当每次窗口右移的时候,需要把右边的新位置加到窗口中的和中,把左边被移除的位置从窗口的和中减掉。这样窗口里面所有元素的和是准确的,我们求出最大的和,最终除以 k 得到最大平均数。
这个方法只用遍历一次数组。
需要注意的是,需要根据 i 的位置,计算滑动窗口是否开始、是否要移除最左边元素:
- 当 i >`= k - 1 时,最左边第一个滑动窗口内的元素刚好 k 个,开始计算滑动窗口的最大和。
- 当 i >`= k 时,为了固定窗口的元素是 k 个,每次移动时需要将 i - k 位置的元素移除。
使用Python2 写的代码如下。
class Solution(object):
def findMaxAverage(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: float
"""
sums = 0
largest = float('-inf')
for i, num in enumerate(nums):
sums += num
if i >= k:
sums -= nums[i - k]
if i >= k - 1:
largest = max(sums, largest)
return largest / float(k)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
刷题心得
今天的题目非常好,虽然是个 Easy 题目,但是让我们练习了 preSum 和 滑动窗口 两种方法的最基本用法。
- preSum 方法要注意定义的 preSum 是否包含当前元素;
- 滑动窗口 方法要注意窗口的大小要固定为 k。
任何组织或个人未经作者授权不得转发
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发