Redis为了支持有序集合Sorted Set,采用了跳表skiplist这种数据结构,能够实现O(logN)的插入效率,同时O(logN)+M的效率查询一定范围内的元素。
skiplist设计与实现
skiplist本质上是一种特殊的列表,只不过列表中的每个节点包含多层,看看跳表节点的数据结构:
typedef struct zskiplistNode {
sds ele;
double score;
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
ele:节点的key值
score:节点的大小,根据这个值对节点排序
backward:该节点的后一个节点,便于反向遍历
level[]:节点的层次数组,数组中每个值表示该层的下一个节点已经该层的跨度
再看看跳表的数据结构:
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
header、tail:跳表的头尾节点,不存储数据,同时level是最大的层数
length:跳表中节点个数
level:跳表节点中最大的层数
借鉴大佬的图,Redis中一个可能的跳表结构如下:
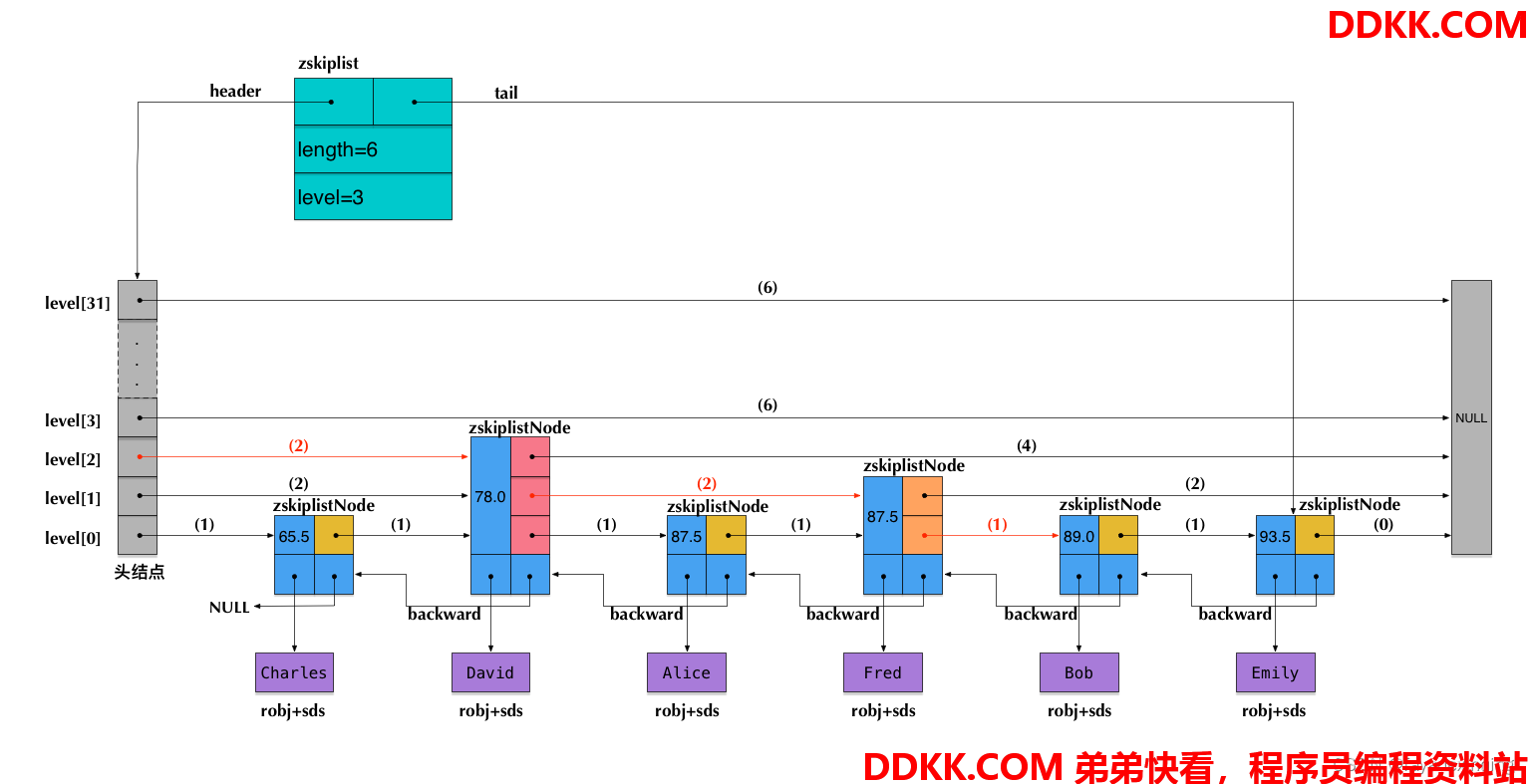
skiplist相关API实现
数据结构清楚了,相关API就清晰了,先看看节点插入zslInsert,先寻找待插入节点在各层次上的前置节点,然后插入节点,最后更新前置节点
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;
// 计算待插入节点与header的距离span
// 计算待插入节点在各个level上的前一个节点
for (i = zsl->level-1; i >= 0; i--) {
/* store rank that is crossed to reach the insert position */
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
update[i] = x;
}
/* we assume the element is not already inside, since we allow duplicated
* scores, reinserting the same element should never happen since the
* caller of zslInsert() should test in the hash table if the element is
* already inside or not. */
// 创建待插入节点,注意:level是根据一定概率生成:
// level=1的概率是50%,level=2的概率是25%,level=3的概率是12.5%,以此类推
level = zslRandomLevel();
if (level > zsl->level) {
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
x = zslCreateNode(level,score,ele);
// 把创建好的节点插入到skiplist中
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
/* update span covered by update[i] as x is inserted here */
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
/* increment span for untouched levels */
// 更新前置节点的span
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
// 更新后置节点
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
zsl->length++;
return x;
}
删除操作比较简单,从skiplist中直接移除该节点,然后释放内存即可
最后再看看指定排序值rank,获取对应节点zslGetElementByRank,从最高层开始遍历,找到该层上对应rank的前置节点,继续向该节点的下一层遍历:
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
zskiplistNode *x;
unsigned long traversed = 0;
int i;
x = zsl->header;
// 从最高层逐层遍历,找到该层上对应rank的前置节点,继续向该节点的下一层遍历
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
{
traversed += x->level[i].span;
x = x->level[i].forward;
}
if (traversed == rank) {
return x;
}
}
return NULL;
}
zset的实现
有了跳表之后,集合中的数据都是有序的,同时为了能够在O(1)时间内获取待key对应的value,还需要一个dict来单独管理KV对的映射,所以,有序集合zset的最终结构如下:
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
dict中的key和value都是指针,后面的内存和zskiplist公用的是同一份