1. 介绍
跳跃表(skiplist)是一种有序的数据结构,它通过建立多层"索引",从而达到快速访问节点的目的. 跳跃表支持平均O(logN)、最坏O(N)复杂度的节点查找,还可以通过顺序性操作来批量处理节点.
如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员(member)是比较长的字符串时,Redis就会使用跳跃表来作为有序集合键的底层实现.
2. 跳跃表的实现
在redis-3.2.0之前,关于跳跃表的定义在redis.h文件中,而在redis-3.2.0之后(包括该版本),关于跳跃表的定义在server.h文件中.
其中zskiplistNode结构用于表示跳跃表节点,而zskiplist结构用于保存跳跃表的表头信息.
跳跃表节点 zskiplistNode
typedef struct zskiplistNode {
// 保存成员对象的地址
robj *obj;
// 分值
double score;
// 后退指针
struct zskiplistNode *backward;
// 层级,柔型数组
struct zskiplistLevel {
// 前进指针
struct zskiplistNode *forward;
// 跨度
unsigned int span;
} level[];
} zskiplistNode;
跳跃表表头 zskiplist
typedef struct zskiplist {
// header 指向跳跃表的表头节点
// tail 指向跳跃表的表尾节点
struct zskiplistNode *header, *tail;
// 跳跃表的长度或跳跃表节点数量计数器,除去第一个节点
unsigned long length;
// 跳跃表中节点的最大层数,除了第一个节点
int level;
} zskiplist;
下图是一个带有三个节点的跳跃表示意图:
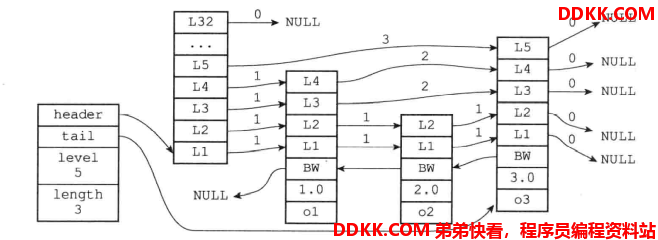
这种画法的层级可能不太好理解,下图的画法更加明朗:
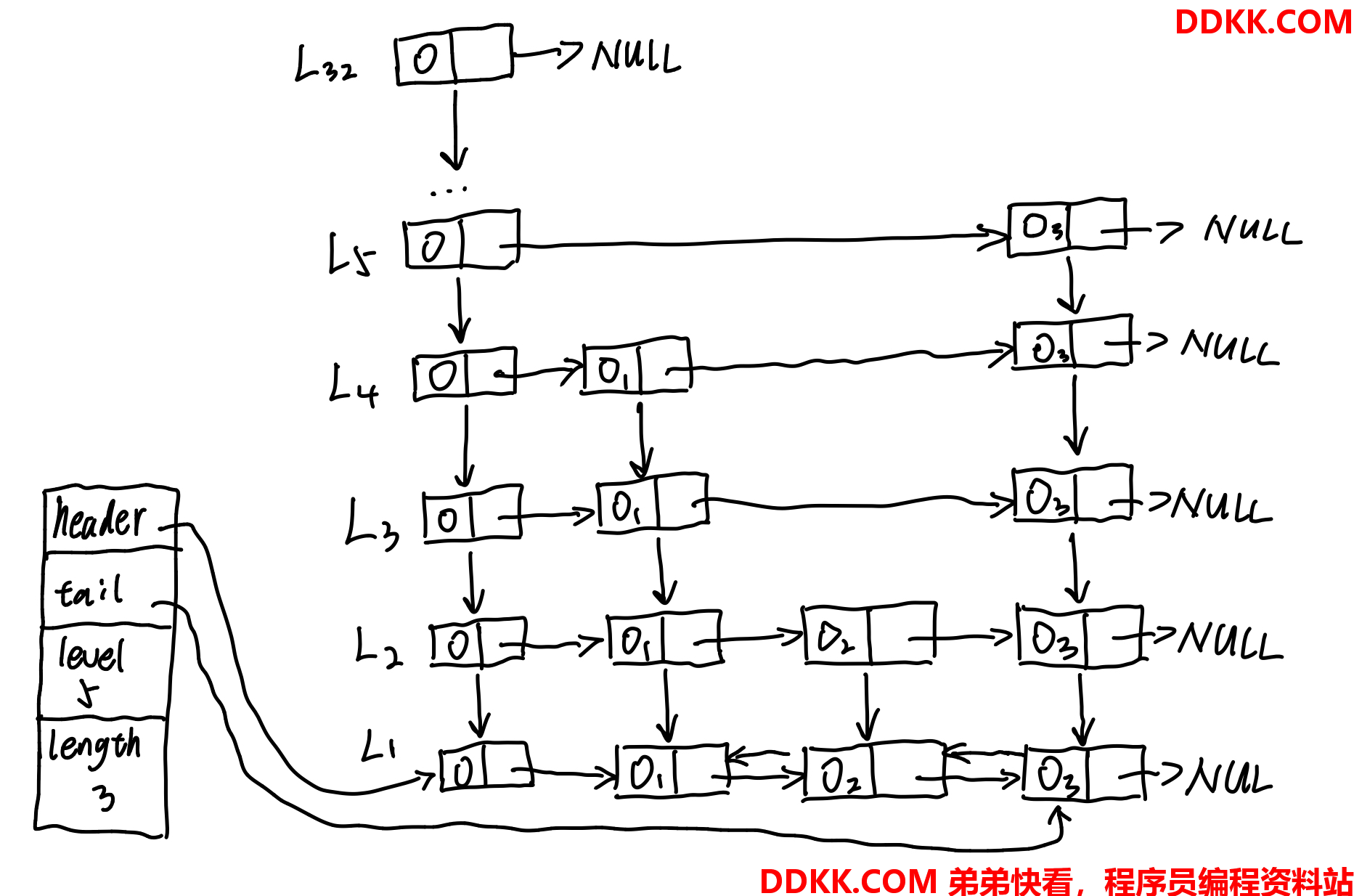
层(level)其实就是跳跃表的索引,Redis的跳表最多可以建立32层索引.
那新插入的节点该建立多少层索引呢?Redis会通过随机算法来计算得到一个随机值,叫做幂次定律.
3. 幂次定律
Redis会为新插入的值返回一个随机层数值. 随机算法使用的是幂次定律.
幂次定律的含义就是:如果某件事的发生频率和它的某个属性成幂关系,那么这个频率就可以称之为符合幂次定律.
特点是:少数几个事件的发生频率占了整个发生频率的大部分, 而其余的大多数事件只占整个发生频率的一个小部分.
映射到Redis中的生成层数就是:一个新插入的节点,生成小数值层数的概率很大,而生成大数值层数的概率很小.
Redis中的这个随机算法在t_zset.c文件中:
#define ZSKIPLIST_MAXLEVEL 32
#define ZSKIPLIST_P 0.25
// 返回一个随机层数值
int zslRandomLevel(void) {
int level = 1;
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
// 返回一个1到32的数字
return (level < ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
概率计算:
p= 0.25
- 层数恰好为1的概率(不执行while)为1 - p.
- 层数恰好为2的概率(执行 1 次while)为p * (1 - p).
- 层数恰好为3的概率(执行 2 次while)为p ^ 2 * (1 - p).
- 层数恰好为4的概率(执行 3 次while)为p ^ 3 * (1 - p).
- 层数恰好为k(k `<= 32)的概率(执行 k - 1 次while)为p ^ (k - 1) * (1 - p).
可以发现生成越高层数的概率会越来越小,而且和上一次呈幂关系递减.
4. 部分源码剖析
4.1 创建跳跃表
创建节点
// 创建一个层数为level,分数为score,对象为obj的跳跃表节点
zskiplistNode *zslCreateNode(int level, double score, robj *obj) {
// 分配空间
zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
// 设置分数
zn->score = score;
// 设置对象
zn->obj = obj;
// 返回节点地址
return zn;
}
创建表头
// 创建返回一个跳跃表 表头zskiplist
zskiplist *zslCreate(void) {
int j;
zskiplist *zsl;
// 分配空间
zsl = zmalloc(sizeof(*zsl));
// 设置默认层数
zsl->level = 1;
// 设置跳跃表长度
zsl->length = 0;
//创建哨兵节点:层数为32,分数为0,没有obj
zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
//跳跃表头节点初始化
for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
// 将跳跃表头节点的所有前进指针forward设置为NULL
zsl->header->level[j].forward = NULL;
// 将跳跃表头节点的所有跨度span设置为0
zsl->header->level[j].span = 0;
}
// 跳跃表头节点的后退指针backward置为NULL
zsl->header->backward = NULL;
// 表头指向跳跃表尾节点的指针置为NULL
zsl->tail = NULL;
return zsl;
}
4.2 销毁跳跃表
销毁一个节点
void zslFreeNode(zskiplistNode *node) {
// 该节点对象的引用计数减1
decrRefCount(node->obj);
// 释放该该节点空间
zfree(node);
}
销毁表头
// 释放跳跃表表头zsl,以及跳跃表节点
void zslFree(zskiplist *zsl) {
zskiplistNode *node = zsl->header->level[0].forward, *next;
// 释放跳跃表的头节点
zfree(zsl->header);
// 释放其他节点
while(node) {
// 备份下一个节点地址
next = node->level[0].forward;
// 释放节点空间
zslFreeNode(node);
// 指向下一个节点
node = next;
}
// 释放表头
zfree(zsl);
}
4.3 插入节点
// 创建一个节点,分数为score,对象为obj,插入到zsl表头管理的跳跃表中,并返回新节点的地址
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
// 记录每一层遍历的时候跨越的节点数
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
// 获取跳跃表头结点地址,从头节点开始一层一层遍历
x = zsl->header;
// 遍历头节点的每个level,从下标最大层减1到0
for (i = zsl->level-1; i >= 0; i--) {
// 更新rank[i]为i+1所跨越的节点数,但是最外一层为0
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
// 这个while循环是查找的过程,沿着x指针遍历跳跃表,满足以下条件则要继续在当前层往前走
while (x->level[i].forward && // 当前层的前进指针不为空且
(x->level[i].forward->score < score || // 当前的要插入的score大于当前层的score或
(x->level[i].forward->score == score && // 当前score等于要插入的score且
compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
//当前层的对象与要插入的obj不等
rank[i] += x->level[i].span; // 记录该层一共跨越了多少节点 加上 上一层遍历所跨越的节点数
x = x->level[i].forward; // 指向下一个节点
}
// while循环跳出时,用update[i]记录第i层所遍历到的最后一个节点,遍历到i=0时,就要在该节点后要插入节点
update[i] = x;
}
// 上述的while中已经确保了同分值且同成员的元素不会出现,所以这里不需要进一步进行检查,可以直接创建新元素
// 获得一个随机的层数
level = zslRandomLevel();
// 如果大于当前所有节点最大的层数时
if (level > zsl->level) {
for (i = zsl->level; i < level; i++) {
// 将大于等于原来zsl->level层以上的rank[]设置为0
rank[i] = 0;
// 将大于等于原来zsl->level层以上update[i]指向头结点(因为这时候的最后一个节点就是头节点)
update[i] = zsl->header;
// update[i]已经指向头结点,将第i层的跨度设置为length
update[i]->level[i].span = zsl->length;
}
// 更新表中的最大层数
zsl->level = level;
}
// 创建一个节点
x = zslCreateNode(level,score,obj);
// 遍历每一层
for (i = 0; i < level; i++) {
// 设置新节点的前进指针为查找时(while循环)每一层最后一个节点的的前进指针
x->level[i].forward = update[i]->level[i].forward;
// 再把查找时每层的最后一个节点的前进指针设置为新创建的节点地址
update[i]->level[i].forward = x;
// 更新插入节点的跨度值
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
// 更新插入节点前一个节点的跨度值
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
// 如果插入节点的level小于原来的zsl->level才会执行
for (i = level; i < zsl->level; i++) {
//因为高度没有达到这些层,所以只需将查找时每层最后一个节点的值的跨度加1
update[i]->level[i].span++;
}
// 设置插入节点的后退指针,就是查找时最下层的最后一个节点,该节点的地址记录在update[0]中
// 如果插入在第二个节点,也就是头结点后的位置就将后退指针设置为NULL
x->backward = (update[0] == zsl->header) ? NULL : update[0];
// 如果x节点不是最尾部的节点
if (x->level[0].forward)
// 就将x节点后面的节点的后退节点设置成为x地址
x->level[0].forward->backward = x;
else
// 否则更新表头的tail指针,指向最尾部的节点x
zsl->tail = x;
// 跳跃表节点计数器加1
zsl->length++;
// 返回x地址
return x;
}
4.4 删除节点
// 删除节点
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
int i;
// 设置前进指针和跨度
// 遍历下标为0到跳跃表最大层数-1的层
for (i = 0; i < zsl->level; i++) {
// 如果找到该节点
if (update[i]->level[i].forward == x) {
// 将前一个节点的跨度减1
update[i]->level[i].span += x->level[i].span - 1;
// 前一个节点的前进指针指向被删除的节点的后一个节点,跳过该节点
update[i]->level[i].forward = x->level[i].forward;
} else {
// 在第i层没找到,只将该层的最后一个节点的跨度减1
update[i]->level[i].span -= 1;
}
}
//设置后退指针
// 如果被删除的前进节点不为空,后面还有节点
if (x->level[0].forward) {
// 就将后面节点的后退指针指向被删除节点x的回退指针
x->level[0].forward->backward = x->backward;
} else {
// 否则直接将被删除的x节点的后退节点设置为表头的tail指针
zsl->tail = x->backward;
}
// 更新跳跃表最大层数
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
zsl->level--;
//节点计数器减1
zsl->length--;
}
4.5 获取节点的排位
// 查找score和o对象在跳跃表中的排位
unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) {
zskiplistNode *x;
unsigned long rank = 0;
int i;
// 遍历头结点的每一层
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score || //只要分值还小于给定的score或者
(x->level[i].forward->score == score && // 分值相等但是对象小于给定对象o
compareStringObjects(x->level[i].forward->obj,o) <= 0))) {
rank += x->level[i].span; // 更新排位值
x = x->level[i].forward; // 指向下一个节点
}
// 确保在第i层找到分值相同,且对象相同时才会返回排位值
if (x->obj && equalStringObjects(x->obj,o)) {
return rank;
}
}
// 没找到
return 0;
}
4.6 范围操作
返回一个zset是否有一部分在range的范围内
int zslIsInLexRange(zskiplist *zsl, zlexrangespec *range) {
zskiplistNode *x;
// 测试range的范围是否合法
if (compareStringObjectsForLexRange(range->min,range->max) > 1 ||
(compareStringObjects(range->min,range->max) == 0 &&
(range->minex || range->maxex)))
return 0;
x = zsl->tail;
// 查看跳跃表的尾节点的对象是否比range的最小值还大,
if (x == NULL || !zslLexValueGteMin(x->obj,range))
// 说明zset没有一部分在range范围
return 0;
x = zsl->header->level[0].forward;
// 查看跳跃表的头节点的对象是否比range的最大值还小,
if (x == NULL || !zslLexValueLteMax(x->obj,range))
// 说明zset没有一部分在range范围
return 0;
return 1;
}
返回第一个包含在range范围内的节点的地址
zskiplistNode *zslFirstInLexRange(zskiplist *zsl, zlexrangespec *range) {
zskiplistNode *x;
int i;
// zsl是否有一部分包含在range内,没有则返回NULL
if (!zslIsInLexRange(zsl,range)) return NULL;
// 遍历每一层
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
// 一直前进寻找,当某一个节点比range的最小值大时,停止寻找
while (x->level[i].forward && !zslLexValueGteMin(x->level[i].forward->obj,range))
x = x->level[i].forward;
}
// 保存当前节点地址
x = x->level[0].forward;
serverAssert(x != NULL);
// 检查当前节点是否超过最大值,超过则返回NULL
if (!zslLexValueLteMax(x->obj,range)) return NULL;
return x;
}