题目地址:https://leetcode-cn.com/problems/maximum-nesting-depth-of-two-valid-parentheses-strings/
题目描述
有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末「有效括号字符串」部分。
嵌套深度 depth 定义:即有效括号字符串嵌套的层数,depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。
给你一个「有效括号字符串」 seq,请你将其分成两个不相交的有效括号字符串,A 和 B,并使这两个字符串的深度最小。
- 不相交:每个 seq[i] 只能分给 A 和 B 二者中的一个,不能既属于 A 也属于 B 。
- A 或 B 中的元素在原字符串中可以不连续。
- A.length + B.length = seq.length
- max(depth(A), depth(B)) 的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示,编码规则如下:
- answer[i] = 0,seq[i] 分给 A 。
- answer[i] = 1,seq[i] 分给 B 。 如果存在多个满足要求的答案,只需返回其中任意 一个 即可。
示例1:
输入:seq = "(()())"
输出:[0,1,1,1,1,0]
示例2:
输入:seq = "()(())()"
输出:[0,0,0,1,1,0,1,1]
提示:
1、1<=text.size<=10000;
有效括号字符串:
仅由 "(" 和 ")" 构成的字符串,对于每个左括号,都能找到与之对应的右括号,反之亦然。
下述几种情况同样属于有效括号字符串:
1. 空字符串
2. 连接,可以记作 AB(A 与 B 连接),其中 A 和 B 都是有效括号字符串
3. 嵌套,可以记作 (A),其中 A 是有效括号字符串
嵌套深度:
类似地,我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S):
1. s 为空时,depth("") = 0
2. s 为 A 与 B 连接时,depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是有效括号字符串
3. s 为嵌套情况,depth("(" + A + ")") = 1 + depth(A),其中 A 是有效括号字符串
例如:"","()()",和 "()(()())" 都是有效括号字符串,嵌套深度分别为 0,1,2,而 ")(" 和 "(()" 都不是有效括号字符串。
大家反馈看不懂题目,所以今天题目已经被修改了,下面以最新题目为讲解。
题目讲解
题目已经讲解了“有效括号字符串”和“嵌套深度”,相信大家都能理解。主要的是“划分规则“和”返回结果“没懂。
划分规则讲解
已知输入是个“有效括号字符串”,现在要把输入“分成两个不相交的有效括号字符串”。其实就是把输入字符串划分成两个有效括号字符串 A 和 B。
题目说的“不相交”有点多余,就像给两个小朋友分糖果🍬,肯定不能把一个糖果🍬同时分给两个小朋友啊。题目就把这种分配方式叫做“不相交”。
返回结果讲解
返回结果是要求只包含 0 或者 1 的数组,标记了每个 ( 或者 ) 应该划分给 A 或者 B。
如果一个字符划分给 A 那么就把字符对应的输出为 0,如果划分给 B 那么就把字符对应的输出为 1.
解题方法
题目要求划分成两个有效括号字符串的深度最小,那么只需要让每个有效括号字符串的深度都尽可能低,即 A 和 B 的最大括号嵌套的深度应该最低。所以我们要使这两个字符串的括号深度尽可能均匀。
从左到右遍历字符串,需要知道 A 和 B 加在一起总的未补全的左括号的数目,让这些未补全的左括号尽量平分给 A 和 B。
所以,重点就是 A 和 B 根据总的未补全的左括号轮流认领新的左括号就行了。
具体做法:
1、 遇到左括号,如果未补全的左括号个数是奇数,把新的左括号给A,如果未补全的左括号个数是偶数,把新的左括号给B并且会让未补全的左括号数目加一;
2、 遇到右括号,右括号属于A或者B呢?和最后一个左括号分配给A或者B一致并且会让未补全的左括号数目减一;
看下题目的示例:
示例1:
输入:seq = "(()())"
输出:[0,1,1,1,1,0]
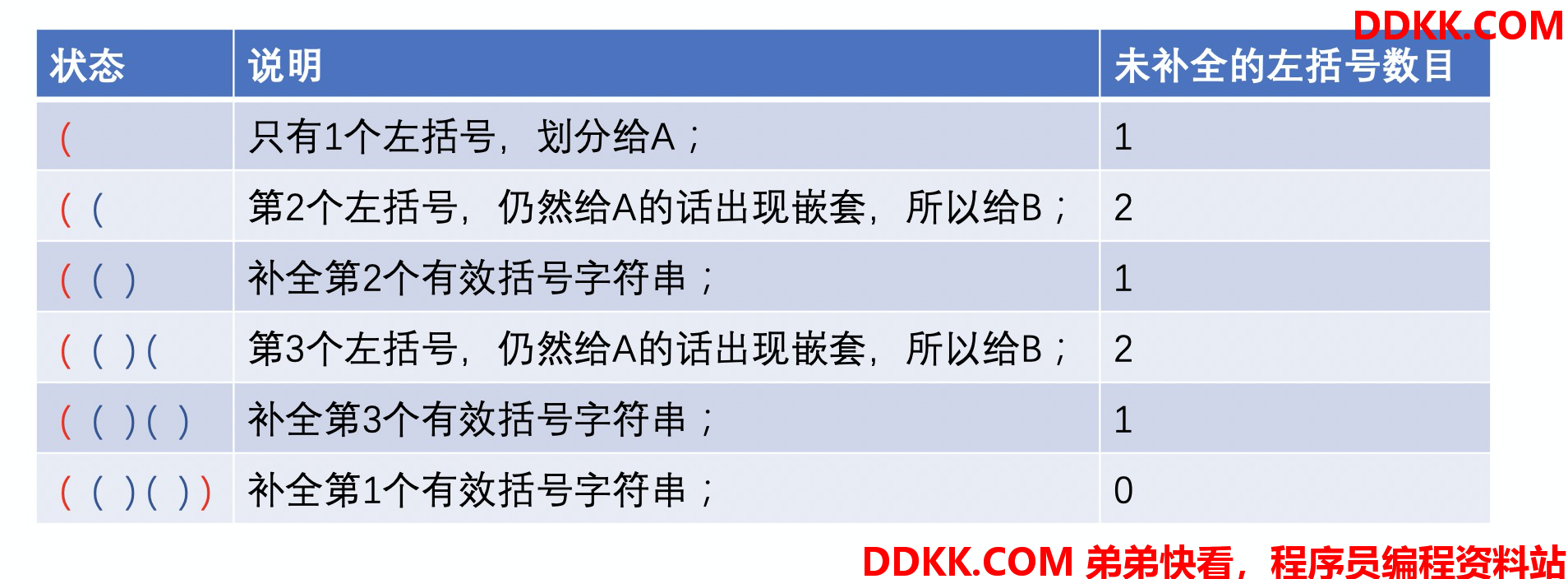
把输入分成了两个字符串,红色的 A 和 蓝色的 B。这样划分之后红色的深度是 1, 蓝色的深度也是 1. 如下图所示。 
示例2:
输入:seq = "()(())()"
输出:[0,0,0,1,1,0,1,1]
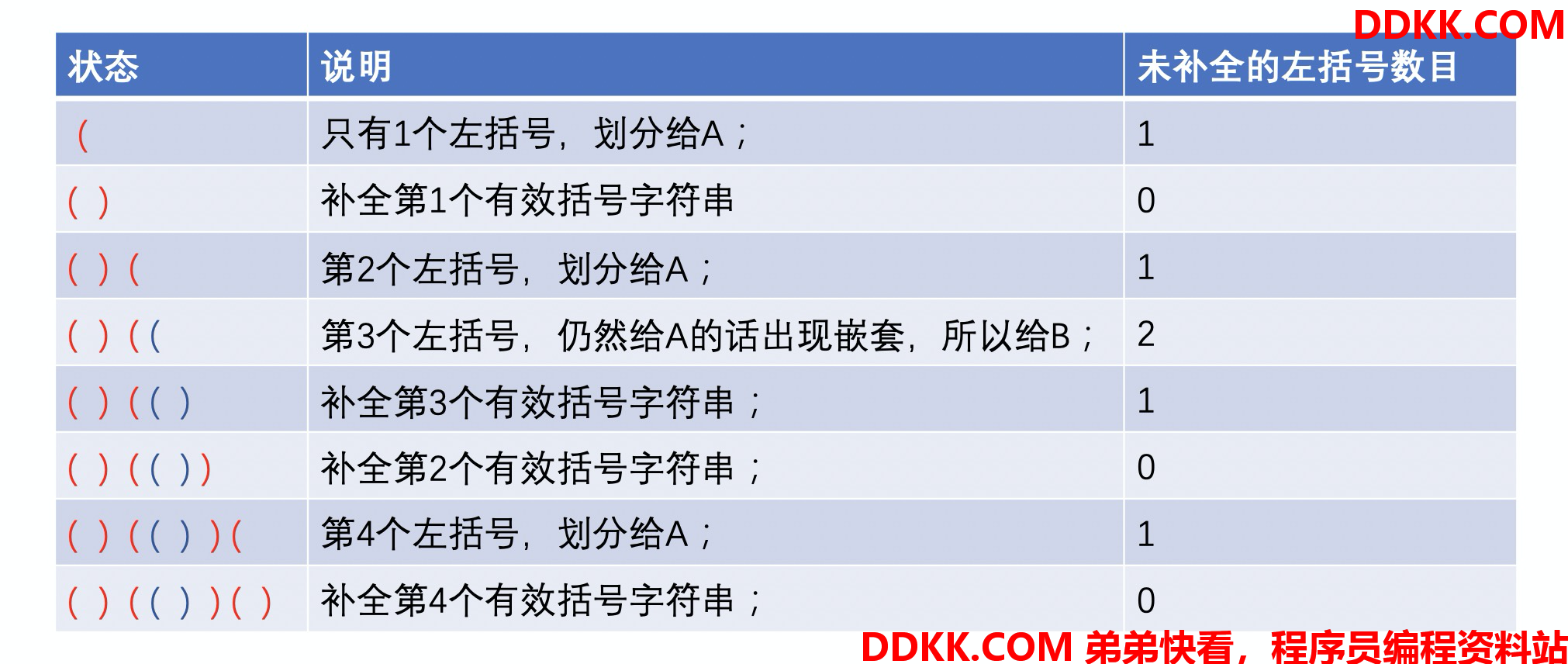
把输入分成了两个字符串,红色的 A 和 蓝色的 B。这样划分之后红色的深度是 1, 蓝色的深度也是 1. 题目的输出只是其中一种结果,下面两种划分分式都可以通过题目测试。如下图所示。 
代码
根据上面的分析,我们不需要使用栈结构,只需要记录当前未补全的左括号数目就知道应该把 A 和 B 分配给谁了。
代码注释很详细,相信你一定能看懂。
C++代码如下。
class Solution {
public:
vector<int> maxDepthAfterSplit(string seq) {
const int N = seq.size();
// 结果
vector<int> res(N, 0);
// 未补全的左括号数
int count = 0;
// 当前遍历到的结果的位置
int pos = 0;
// 遍历每个字符
for (char c : seq) {
if (c == '(') {
// 未补全的左括号数增加了
count ++;
// 如果未补全的左括号数是奇数,当前新的左括号分配给A,结果中写0;
// 如果未补全的左括号数是偶数,当前新的左括号分配给B,结果中写1;
res[pos] = 1 - count % 2;
} else {
// 右括号属于A或者B呢?和最后一个左括号分配给A或者B一致
res[pos] = 1 - count % 2;
// 未补全的左括号数减少了
count --;
}
// 结果的位置跟当前遍历到的字符相一致
pos ++;
}
return res;
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发