题目地址:https://leetcode-cn.com/problems/connecting-cities-with-minimum-cost/
题目描述
There are N cities numbered from 1 to N.
Youare given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. (A connection is bidirectional: connecting city1 and city2 is the same as connecting city2 and city1.)
Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.
Example 1:
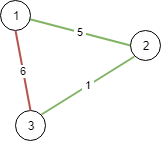
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
Output: 6
Explanation:
Choosing any 2 edges will connect all cities so we choose the minimum 2.
Example 2:
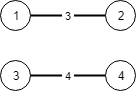
Input: N = 4, connections = [[1,2,3],[3,4,4]]
Output: -1
Explanation:
There is no way to connect all cities even if all edges are used.
Note:
1、1<=N<=10000;
2、1<=connections.length<=10000;
3、1<=connections[i][0],connections[i][3]<=N;
4、0<=connections[i][2]<=10^5;
5、connections[i][0]!=connections[i][4];
题目大意
想象一下你是个城市基建规划者,地图上有 N 座城市,它们按以 1 到 N 的次序编号。 给你一些可连接的选项 conections,其中每个选项 conections[i] = [city1, city2, cost] 表示将城市 city1 和城市 city2 连接所要的成本。(连接是双向的,也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连)。 返回使得每对城市间都存在将它们连接在一起的连通路径(可能长度为 1 的)最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务,则请你返回 -1。
解题方法
Kruskal算法
本题是标准的最小生成树问题,有Prim和Kruskal算法两个解法。
MST(Minimum Spanning Tree,最小生成树)问题有两种通用的解法,Prim算法就是其中之一,它是从点的方面考虑构建一颗MST,大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。至于怎么合并到一个集合,那么这里我们就可以用到一个工具——-并查集。换而言之,Kruskal算法就是基于并查集的贪心算法。
具体做法如上所言,不再赘述。
C++代码如下:
class Solution {
public:
int minimumCost(int N, vector<vector<int>>& connections) {
part = N;
parent = vector<int>(N, 0);
for (int i = 0; i < N; ++i)
parent[i] = i;
sort(connections.begin(), connections.end(),
[](const vector<int>& a, const vector<int>& b) { return a[2] < b[2];});
int res = 0;
for (vector<int>& conn : connections) {
int a = conn[0] - 1;
int b = conn[1] - 1;
int cost = conn[2];
int pa = find(a);
int pb = find(b);
if (pa != pb) {
uni(a, b);
res += cost;
}
if (part == 1)
return res;
}
return -1;
}
int find(int a) {
if (parent[a] == a)
return a;
return find(parent[a]);
}
void uni(int a, int b) {
int pa = find(a);
int pb = find(b);
if (pa == pb)
return;
parent[pa] = pb;
part --;
}
private:
vector<int> parent;
int part = 0;
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
参考资料: https://www.cnblogs.com/fzl194/p/8722989.html https://www.cnblogs.com/fzl194/p/8723325.html
2022
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发