题目地址:https://leetcode.com/problems/coin-change/description/
题目描述
Youare given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
Example 1:
Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
Example 2:
Input: coins = [2], amount = 3
Output: -1
Note:
1、 Youmayassumethatyouhaveaninfinitenumberofeachkindofcoin.;
题目大意
给了无限数量的面值分别为coins的硬币,问能否构成amuont。
解题方法
动态规划
题目比较重要的是硬币无限数量。我们的做法是使用动态规划,需要构建一个长度是amount + 1的dp数组,其含义是能够成面额从0到amount + 1需要使用的最少硬币数量。
所以我们对每一种面额的硬币,都去计算并更新新添了这种面额的情况下,构成的所有面额需要的最少硬币数量。注意,变量是不同面额的硬币。dp更新的策略是从coin面额到amount+1的面额依次向后查找,看这个位置能不能用更少的硬币组成(即使用面额是i - coin的需要硬币数量+1).
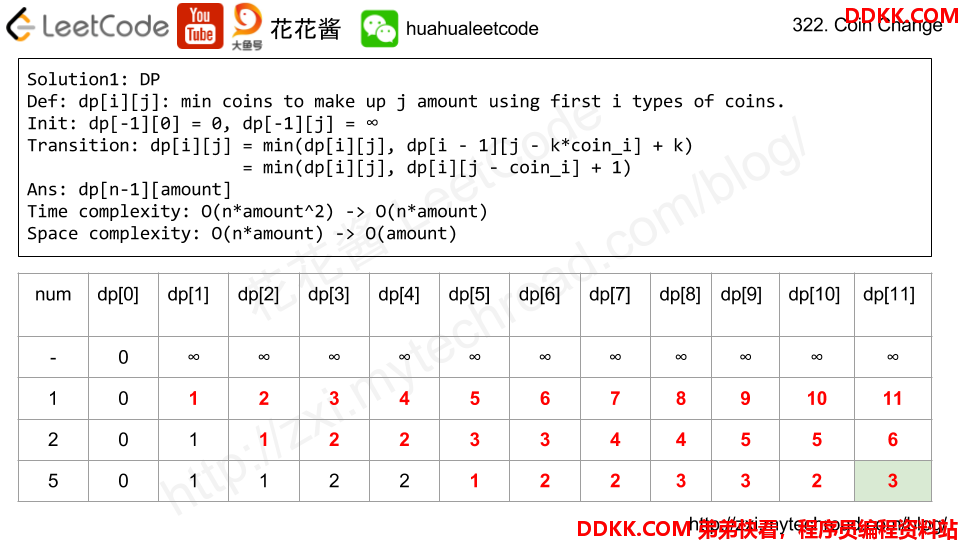
时间复杂度很小,但是不会算,空间复杂度是O(1).
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for i in range(coin, amount + 1):
if dp[i - coin] != float('inf'):
dp[i] = min(dp[i], dp[i - coin] + 1)
return -1 if dp[amount] == float('inf') else dp[amount]
1 2 3 4 5 6 7 8 9 10 11 12 13 14
C++代码如下:
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
const int N = coins.size();
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int coin : coins) {
for (int i = coin; i <= amount; ++i) {
if (dp[i - coin] != INT_MAX) {
dp[i] = min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
参考资料:
https://www.youtube.com/watch?v=uUETHdijzkA https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-322-coin-change/
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发