一、门电路
用以实现基本逻辑运算和复合逻辑运算的单元电路称为门电路。上一部分我们已经知道了逻辑门电路的概念(逻辑运算、继电器和门电路),并且引出了一个基础的门电路:与门
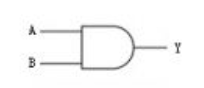
事实上,常用的门电路有很多,除了我们之前介绍的与门,还有或门、非门、与非门、或非门等等,我们的目的是简单介绍门电路在计算机中的应用,现在不用探究的太深刻,如果感兴趣的同学可以自行查阅相关资料(推荐书籍<<编码的奥秘>>)。
与门的真值表其实就对应一个简单的串联电路输出的真值表,如下图所示(表示只有当两个输入为1时,输出才为1):

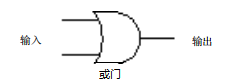
对应的或门也类似,对应了并联电路输出的真值表(表示只有当两个输入为0是,输出才为0):

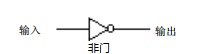
而且它也有自己的特殊符号,相应的非门等其它门电路也是如此,只是非门的真值表看起来要简单的多(就是单纯的取反,所以我们一般都称之为反向器):
二、半加器
接下来,我们尝试使用基础门电路实现一个加法器。首先,我们需要明确,什么叫做加法器?它需要实现什么样的功能?所幸我们还是明白,加法器肯定是做加法的,毕竟加法是最基本的运算,它的功能就是将两个数加起来(多个数相加也是两个一组相加,将结果和其它数继续相加)。而当我们实现了加法器之后,你会发现,其实计算机做的运算就只有一个,那就是加法,我们通过加法器可以实现减法、乘法、除法等等。我们接下来就来实现一个二进制加法器(二进制相关内容,这里有介绍)。
我们首先来考虑一位的情况(输出用两位存储),做个简单描述:
0+0=00
1+0=01
0+1=01
1+1=10
我们可以自然定义一些东西:两个数相加,会产生两个结果,一个是和位,一个是进位。比如1+1,和位是0,进位是1;1+0的和位是1,进位则是0;0+0的和位与进位都是0。一个加法运算,二进制和十进制性质都一样,如果我们列个算术式出来,都是从最右边一列开始,逐列相加两个数,进位会和下一次的加法一起参与运算,就像下面这样:

先想想进位输出有什么特点?那很明显,只有当两个数都是1的时候,进位才是1,其它情况都为0(参考上面1位相加的结果描述)。那和位呢?同样参照该描述,只有两个输入不相同的时候,和位才是1,否则是0。
根据上面的介绍,我们现在要设计的加法器,需要接受两个输入,经过一些"运算"需要产生两个输出(和位和进位):
进位很简单,我们的基础门电路:与门,就可以实现其功能,因为与门恰好满足其特征:仅当两个输入为1时,输出才是1。所以我们的进位这部分就设计好了,就是一个简单的与门,很简单吧?那么和位呢?我们介绍的与、或、非,三个门电路没有任何一个门电路具备这样的特征,这时候就需要我们手动构建一个满足该特征的门电路出来。
在构建之前,再想想其特征:当且仅当两个输入不同的时候,输出才是1。和我们的与或非三个基本门电路挨着比对:
非门?八竿子打不到一堆儿去。
与门?好像差的有点儿远(到是和与门再取反有点儿关系哦)。
或门?咦?我们发现如果或门的输出中,把两个输入都为1的情况排除出去,就是我们的要求了啊!(如果想不明白的可以自行画画对应的真值表对比看看,一目了然)。
可是怎么排除呢?我们就要来做一个组合,目的就是排除掉输入同时为1的情况,那么我们怎么判断这种情况呢?那就是用与门,如果两个输入经过与门逻辑,输出是1,那么就说明两个输入同时为1,这时候我们就需要做一些特殊处理。怎么处理呢?我们转换一下思维,根据与门的特点,如果我们把与门的结果取反,得到的结果就是:当且仅当两个输入相同时,输出才是0,而我们正好要排除掉或门中两个输入相同的情况,怎么排除呢?和0做与操作是最简单的做法。所以我们可以把与门的结果取反,再和或门的结果作为又一个与门的输入,这是输出就是我们想要的结果,下面通过图形描述一下(结合进位输出)(注:如果有感兴趣的同学,可以试试以与门为基础进行改造,你会发现构造出来的电路图和以或门为基础构造的电路图一模一样,区别只是参照物不一样而已):
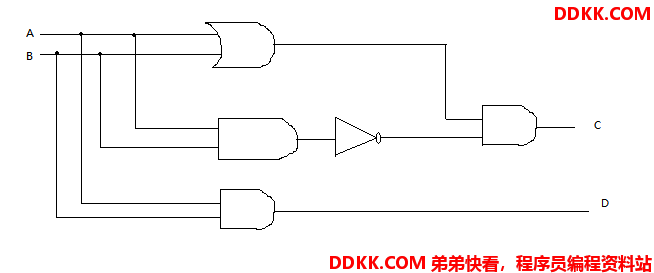
其中,A和B分别为两个输入,C为和位输出,D为进位输出(用windows画图工具画的,请忽略图形不标准o(╯□╰)o)。如果我们把门电路符号换成具体的继电器,那么就是一个完整的电路图,已经可以实现我们的一些基本要求了。还有一点需要说明,我们通过几个基础的门电路组合了一下,实现了和位输出的要求,我们画出来很复杂,用了一个或门,一个非门,两个与门,其实这个电路有它自己的名字,叫做"异或门",它表示只有两个输入不相同时,输出才是1。电气工程师也认为这样画出来太麻烦,于是又设计了一个特殊的符号来表示这个"异或门"。同样,他们也是懒到了极致,一个与门和非门的组合,也懒得画,同样设计了一个特殊的符号表示这样的组合,叫做"与非门",相应的还有或非门等等。如下图所示:
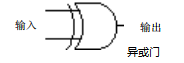
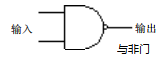
所以上面的复杂图示,可以简化为如下:
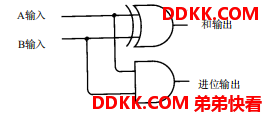
到这里,我们已经实现了一个具备加法性质的逻辑电路图了,这样看起来不错,起码看起来很简洁,的确,这个逻辑电路图就是我们听到的"半加器",简单表示为:
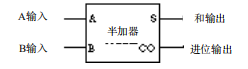
三、全加器
上面提到的半加器可以把两个二进制位A 和 B相加,从而得到一个和输出 (简称S) 和一个进位输出 (简称CO)。但大部分二进制数是多于 1位的,半加器不能够把前一步的进位加到本次运算中。这是什么意思呢?我们回想刚开始我们所描述的加法,进位需要参加下一次的加法运算中,按照这个理解,我们的输入端不应该是两位,而应该是三位,除了A和B输入之外,还应该有上次运算的进位输出才对,不然我们即使把多个半加器组合起来实现多位二进制数的加法,得到的结果在有进位的情况下,也肯定是错误的。比如11+11,正确的结果应该是:110,但是按照这个逻辑图的结果却是:100。那么怎么加入进位呢?
要实现我们的目的,可以先想象一下,既然我们的输入需要增加上一个运算的进位,而本次运算也会产生一个和位和进位,那么上一个进位输出和本次运算产生的和位与进位该怎样进行的运算呢?显然,上一次的进位首先应该要和本次的和位做一次"半加"操作,这次"半加"操作输出的和位,就是本次最终的和位;而输出的进位和上一次的进位需要用或门连接起来,但是为什么是或门呢?因为当你把所有情况都考虑完,你会发现两个进位不可能同时为1,就像十进制中两个个位数相加,不会达到20一样(最多就是9+9=18),所以上次进位和本次进位,只要有一个进位是1,我们就可以认为最终进位就是1了,当然也可以再加一个半加器,但是的确没有必要,然后本次的进位又会参与到下次的计算中去。按照这个思想把半加器和或门连接起来:
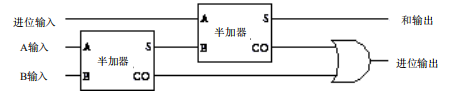
和半加器一样,我们依然简化一下这个图形描述:
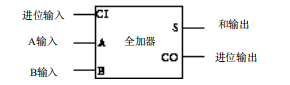
我们称其为全加器,如果我们要实现一个8位数的加法器,该怎么设计电路呢?这个没有什么复杂的,只需要把8个全加器级联起来,连接的标准就是,当前全加器的和位输出保存下来,进位输出作为下一个全加器的输入,那么第一个全加器的进位输出置零即可。如下图所示:
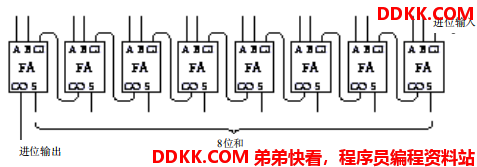
一旦构建了一个8位的全加器,只需要按照相同的方式级联起来,可以很容易的构建一个16位甚至更高位的加法器。现在我们可以算一下,一个支持8位的全加器需要多少个继电器呢?首先,每个与门、或门、与非门都需要2个继电器,所以,一个异或门需 6个继电器。一个半加器由一个异或门和一个与门构成,所以它要 8个继电器。1个全加器需要两个半加器和一个或门,所以它要 1 8个继电器。对于8位二进制加法机而言,共需 8个全加器,因而总共是144个继电器。
(摘自<<编码的奥秘>>)现在,你可能会问:“计算机真的是以这种方式把数字加起来的吗?” 基本上是这样的,但不完全是。
首先,加法器应该做得更快。如果你明白这个电路是如何工作的,你会看到最低位相加产生的进位作为下一列数相加的一个输入,而第 3列的加法又等着第 2列加法的进位,依此类推。加法器总体的速度等于加数的位数乘以单个全加器的速度。这种进位方式称为行波进位。更快的加法器使用称为先行进位的加法电路,从而加快了加法进程。
第二(但是十分重要)计算机再也不用继电器了!尽管它们曾经用过。建于 20世纪30年代初的第一批数字计算机使用继电器,后来又用了真空管。现代计算机用晶体管。当用在计算机中时,晶体管和继电器的功能差不多,但是晶体管速度更快,体积更小,更安静,更省电,而且还便宜不少。构造一个 8位加法器仍然需要 144个晶体管(如果采用先行进位,则需要更多),但整体电路的体积却小多了。
四、总结
这里我们介绍了怎么用基础门电路构建一个具备加法功能的逻辑电路,这个是计算机做所有运算的基础。计算机基础这块儿就先总结到这里,毕竟这些内容也比较枯燥,如果有同学感兴趣,可以自行查阅相关资料或者留言告知。
注:部分内容参考自:<<编码的奥秘>>