题目地址: https://leetcode.com/problems/domino-and-tromino-tiling/description/
题目描述:
Wehave two types of tiles: a 2x1 domino shape, and an "L" tromino shape. These shapes may be rotated.
XX <- domino
XX <- "L" tromino
X
Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.
(Ina tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)
Example:
Input: 3
Output: 5
Explanation:
The five different ways are listed below, different letters indicates different tiles:
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY
Note:
1、 Nwillbeinrange[1,1000].;
题目大意
有个2N的长条,在里面堆放两种骨牌:一种是12的长方形,另一种是L形的,均有无限多个。问总的有多少种堆叠方式。
解题方法
看到要模一个数,说明结果很大,肯定需要使用DP求解。这个DP的转移方程不好找。下面的分析来自花花酱open in new window,
先找一下规律,如果只有一种长方形的长条的话,那么递推公式是这样的:
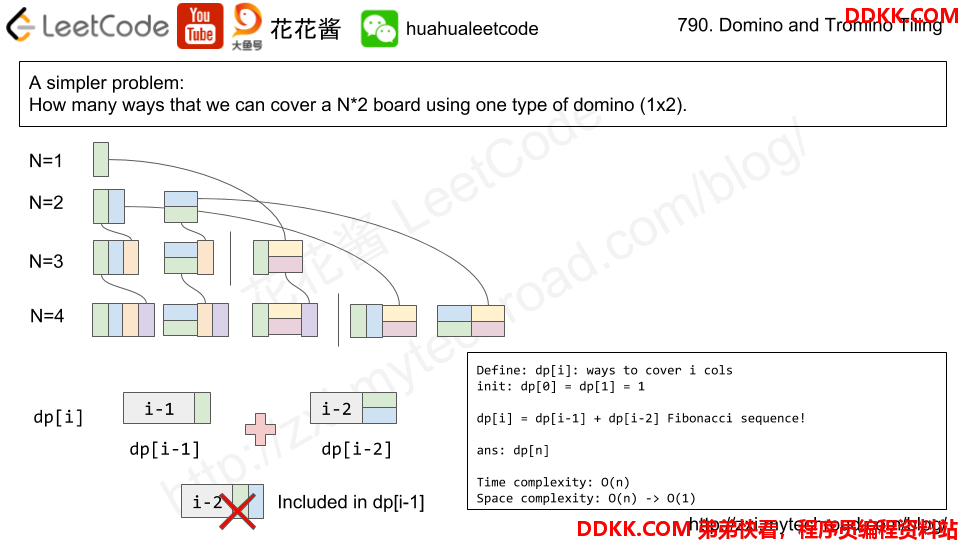
当有两种长条的时候,同样的道理能得到这种状态的递推公式。
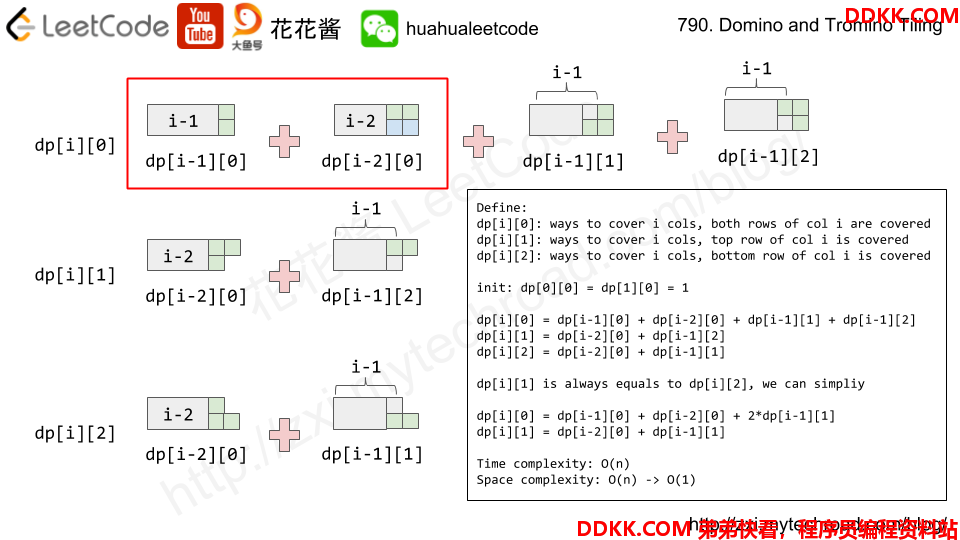
更详细的讲解要看花花酱的视频open in new window,我就不班门弄斧了。
时间复杂度是O(N),空间复杂度是O(N)。
class Solution:
def numTilings(self, N):
"""
:type N: int
:rtype: int
"""
dp = [[0] * 2 for _ in range(N + 1)]
dp[0][0] = 1
dp[1][0] = 1
for i in range(2, N + 1):
dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + 2 * dp[i - 1][1]) % (10 ** 9 + 7)
dp[i][1] = (dp[i - 2][0] + dp[i - 1][1]) % (10 ** 9 + 7)
return dp[-1][0]
1 2 3 4 5 6 7 8 9 10 11 12 13
参考资料:
https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-790-domino-and-tromino-tiling/ https://www.youtube.com/watch?v=S-fUTfqrdq8
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发