本文关键词:Leetcode, 力扣,Trie, 前缀树,字典树,208,Python, C++, Java
题目地址:https://leetcode.com/problems/implement-trie-prefix-tree/description/
题目描述
Implement a trie with insert, search, and startsWith methods.
Example:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // returns true
trie.search("app"); // returns false
trie.startsWith("app"); // returns true
trie.insert("app");
trie.search("app"); // returns true
Note:
1、 Youmayassumethatallinputsareconsistoflowercaselettersa-z.;
2、 Allinputsareguaranteedtobenon-emptystrings.;
题目大意
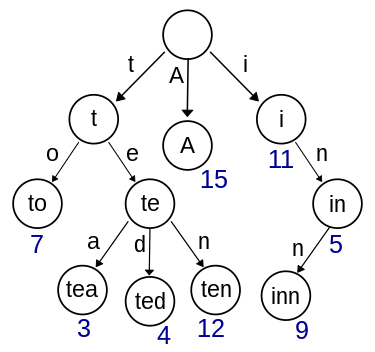
实现字典树。字典树:
上图是一棵Trie树,表示一个保存了8个键的trie结构,"A", "to", "tea", "ted", "ten", "i", "in", and "inn".。
从上图可以归纳出Trie树的基本性质:
1、 根节点不包含字符,除根节点外的每一个子节点都包含一个字符;
2、 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串每个节点的所有子节点包含的字符互不相同;
3、 通常在实现的时候,会在节点结构中设置一个标志,用来标记该结点处是否构成一个单词(关键字);
可以看出,Trie树的关键字一般都是字符串,而且Trie树把每个关键字保存在一条路径上,而不是一个结点中。另外,两个有公共前缀的关键字,在Trie树中前缀部分的路径相同,所以Trie树又叫做前缀树(Prefix Tree)。
解题方法
本文写成前缀树入门教程。
从二叉树说起
前缀树,也是一种树。为了理解前缀树,我们先从二叉树说起。
常见的二叉树结构是下面这样的:
class TreeNode {
int val;
TreeNode* left;
TreeNode* right;
}
1 2 3 4 5
可以看到一个树的节点包含了三个元素:该节点本身的值,左子树的指针,右子树的指针。二叉树可视化是下面这样的:
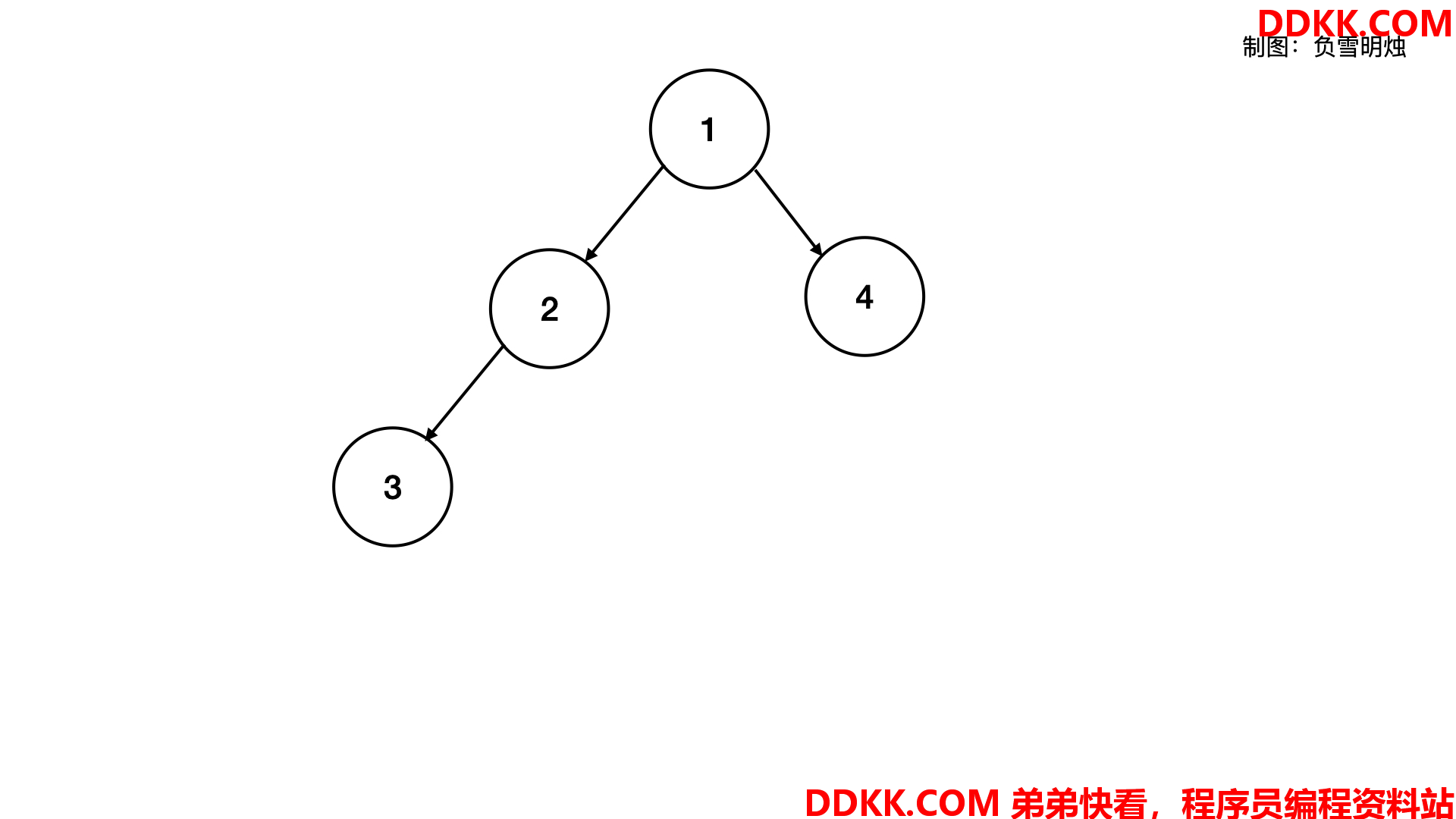
二叉树的每个节点只有两个孩子,那如果每个节点可以有多个孩子呢?这就形成了多叉树。多叉树的子节点数目一般不是固定的,所以会用变长数组来保存所有的子节点的指针。多叉树的结构是下面这样:
class TreeNode {
int val;
vector<TreeNode*> children;
}
1 2 3 4
多叉树可视化是下面这样:
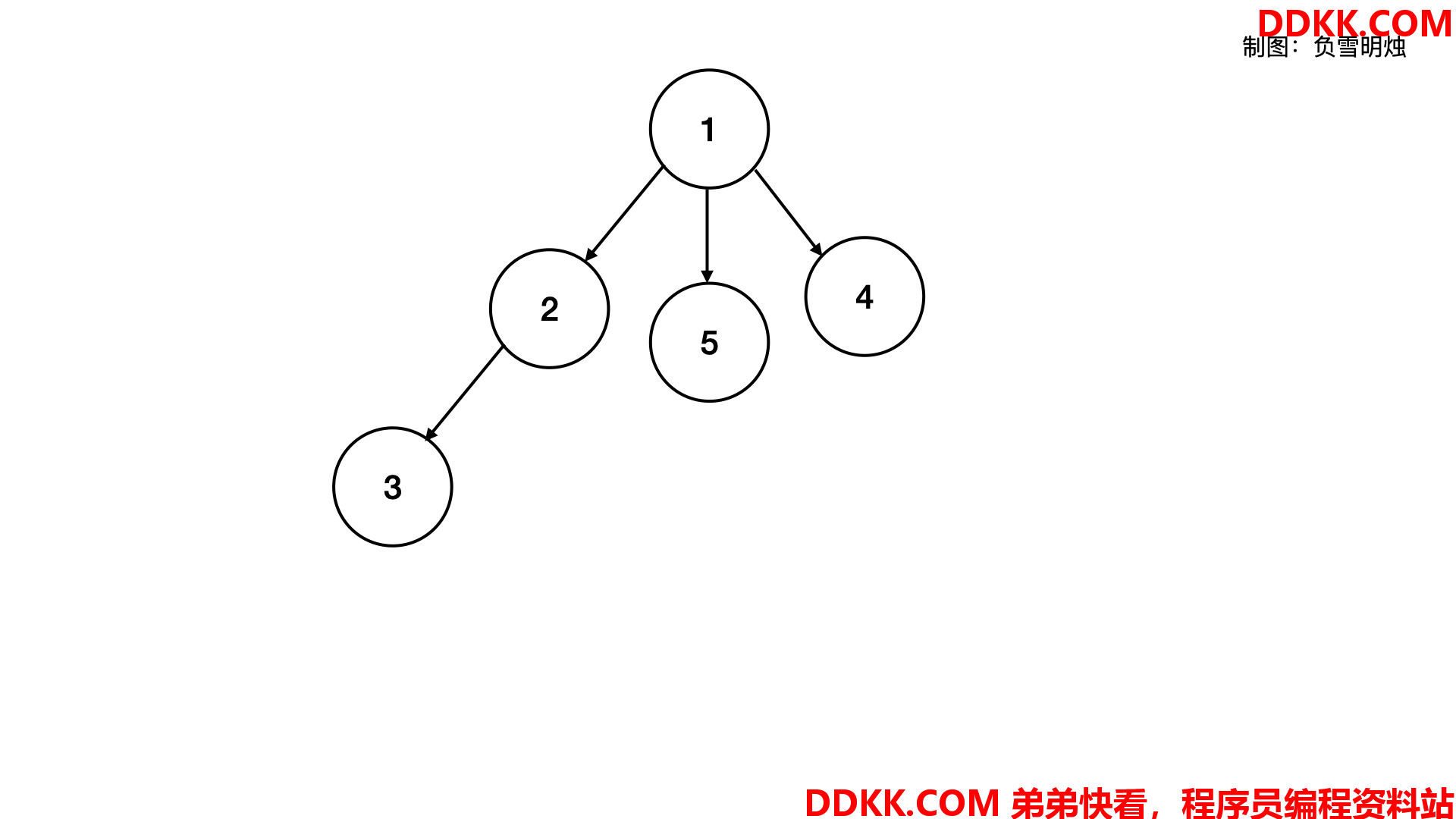
对于普通的多叉树,每个节点的所有子节点可能是没有任何规律的。而本题讨论的「前缀树」就是每个节点的 children 有规律的多叉树。
前缀树
(只保存小写字符的)「前缀树」是一种特殊的多叉树,它的 TrieNode 中 chidren 是一个大小为 26 的一维数组,分别对应了26个英文字符 'a' ~ 'z',也就是说形成了一棵 26叉树。
前缀树的结构可以定义为下面这样。 里面存储了两个信息:
- isWord 表示从根节点到当前节点为止,该路径是否形成了一个有效的字符串。
- children 是该节点的所有子节点。
class TrieNode {
public:
vector<TrieNode*> children;
bool isWord;
TrieNode() : isWord(false), children(26, nullptr) {
}
~TrieNode() {
for (auto& c : children)
delete c;
}
};
1 2 3 4 5 6 7 8 9 10 11
构建
在构建前缀树的时候,按照下面的方法:
- 根节点不保存任何信息;
- 关键词放到「前缀树」时,需要把它拆成各个字符,每个字符按照其在 'a' ~ 'z' 的序号,放在对应的 chidren 里面。下一个字符是当前字符的子节点。
- 一个输入字符串构建「前缀树」结束的时候,需要把该节点的 isWord 标记为 true,说明从根节点到当前节点的路径,构成了一个关键词。
下面是一棵「前缀树」,其中保存了 {"am", "an", "as", "b", "c", "cv"} 这些关键词。图中红色表示 isWord 为 true。 看下面这个图的时候需要注意:
1、 所有以相同字符开头的字符串,会聚合到同一个子树上比如{"am","an","as"};
2、 并不一定是到达叶子节点才形成了一个关键词,只要isWord为true,那么从根节点到当前节点的路径就是关键词比如{"c","cv"};
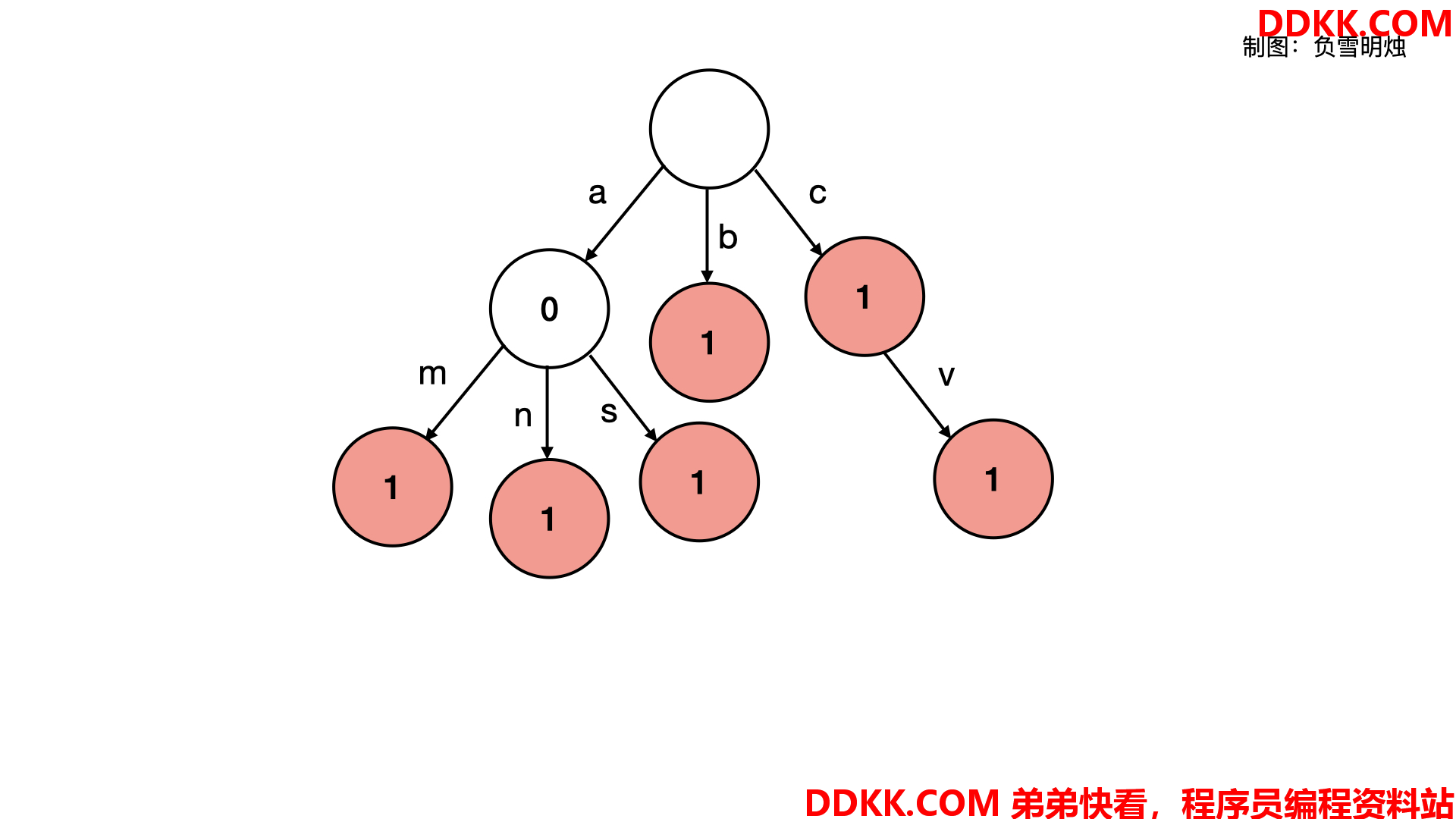
有些题解把字符画在了节点中,我认为是不准确的。因为前缀树是根据 字符在 children 中的位置确定子树,而不真正在树中存储了 'a' ~ 'z' 这些字符。树中每个节点存储的 isWord,表示从根节点到当前节点的路径是否构成了一个关键词。
查询
在判断一个关键词是否在「前缀树」中时,需要依次遍历该关键词所有字符,在前缀树中找出这条路径。可能出现三种情况:
1、 在寻找路径的过程中,发现到某个位置路径断了比如在上面的前缀树图中寻找"d"或者"ar"或者"any",由于树中没有构建对应的节点,那么就查找不到这些关键词;
2、 找到了这条路径,但是最后一个节点的isWord为false这也说明没有改关键词比如在上面的前缀树图中寻找"a";
3、 找到了这条路径,并且最后一个节点的isWord为true这说明前缀树存储了这个关键词,比如上面前缀树图中的"am","cv"等;
应用
上面说了这么多前缀树,那前缀树有什么用呢?
- 比如我们常见的电话拨号键盘,当我们输入一些数字的时候,后面会自动提示以我们的输入数字为开头的所有号码。
- 比如我们的英文输入法,当我们输入半个单词的时候,输入法上面会自动联想和补全后面可能的单词。
- 再比如在搜索框搜索的时候,输入"负雪",后面会联想到 负雪明烛 。
等等。
代码
下面的Python 解法中,保存 children 是使用的字典,它保存的结构是 {字符:Node} ,所以可以直接通过 children['a'] 来获取当前节点的 'a' 子树。
下面的C++ 解法中,保存 children 用的题解分析时讲的大小为 26 的数组实现的。而且我的 C++ 解法中写出了很多人容易忽略的一个细节,就是 TrieNode 析构的时候,需要手动释放内存。
Python 代码如下:
class Node(object):
def __init__(self):
self.children = collections.defaultdict(Node)
self.isword = False
class Trie(object):
def __init__(self):
self.root = Node()
def insert(self, word):
current = self.root
for w in word:
current = current.children[w]
current.isword = True
def search(self, word):
current = self.root
for w in word:
current = current.children.get(w)
if current == None:
return False
return current.isword
def startsWith(self, prefix):
current = self.root
for w in prefix:
current = current.children.get(w)
if current == None:
return False
return True
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
C++代码如下:
class TrieNode {
public:
vector<TrieNode*> children;
bool isWord;
TrieNode() : isWord(false), children(26, nullptr) {
}
~TrieNode() {
for (auto& c : children)
delete c;
}
};
class Trie {
public:
/** Initialize your data structure here. */
Trie() {
root = new TrieNode();
}
/** Inserts a word into the trie. */
void insert(string word) {
TrieNode* p = root;
for (char a : word) {
int i = a - 'a';
if (!p->children[i])
p->children[i] = new TrieNode();
p = p->children[i];
}
p->isWord = true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
TrieNode* p = root;
for (char a : word) {
int i = a - 'a';
if (!p->children[i])
return false;
p = p->children[i];
}
return p->isWord;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
TrieNode* p = root;
for (char a : prefix) {
int i = a - 'a';
if (!p->children[i])
return false;
p = p->children[i];
}
return true;
}
private:
TrieNode* root;
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
- 时间复杂度:O(字符串长度),插入和查询操作需要遍历一次字符串。
- 空间复杂度:O(字符串长度之和)。
刷题心得
前缀树是挺有意思的应用。不过面试和力扣题目都考察不多,建议大家理解掌握,不必深究。
任何组织或个人未经作者授权不得转发
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发