本文关键词:算法题,刷题,Leetcode, 力扣,二叉搜索树,BST,第 k 小的元素,Python, C++, Java
题目地址:https://leetcode.com/problems/kth-smallest-element-in-a-bst/#/descriptionopen in new window
题目描述
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
Note:
- You may assume k is always valid, 1 ≤ k ≤ BST's total elements.
Example 1:
Input: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
Output: 1
Example 2:
Input: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
Output: 3
Follow up:
- What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?
题目大意
找出一个BST中第K小的数字是多少。
解题方法
各位题友大家好! 我是负雪明烛。
今天题目重点只有一个:二叉搜索树(BST)。
遇到二叉搜索树,立刻想到这句话:
「二叉搜索树(BST)的中序遍历是有序的」。
这是解决所有二叉搜索树问题的关键。
题目要求 BST 中第 k 小的元素,等价于求 BST 中序遍历的第 k 个元素。
分享二叉树遍历的模板:先序、中序、后序遍历方式的区别在于把「执行操作」放在两个递归函数的位置。
伪代码在下面。
1、 先序遍历:
def dfs(root):
if not root:
return
执行操作
dfs(root.left)
dfs(root.right)
1 2 3 4 5 6
1、 中序遍历:
def dfs(root):
if not root:
return
dfs(root.left)
执行操作
dfs(root.right)
1 2 3 4 5 6
1、 后序遍历:
def dfs(root):
if not root:
return
dfs(root.left)
dfs(root.right)
执行操作
1 2 3 4 5 6
本题是使用了中序遍历,所以把「执行操作」这一步改成自己想要的代码。
于是有了下面两种写法。
方法一:数组保存中序遍历结果
这个方法是最直观的,也最不容易出错的。
1、 先中序遍历,把结果放在数组中;
2、 最后返回数组的第k个元素;
对应的代码如下,二叉树的各种遍历方式是基本功,务必要掌握。
Java 代码如下:
public class Solution {
List<Integer> list;
public int kthSmallest(TreeNode root, int k) {
list = new ArrayList<Integer>();
dfs(root);
return list.get(k - 1);
}
public void dfs(TreeNode root){
if(root == null){
return;
}
dfs(root.left);
list.add(root.val);
dfs(root.right);
}
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
C++代码如下:
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
vector<int> res;
dfs(root, res);
return res[k - 1];
}
void dfs(TreeNode* root, vector<int>& res) {
if (!root) return;
dfs(root->left, res);
res.push_back(root->val);
dfs(root->right, res);
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Python 语言如下:
class Solution(object):
def kthSmallest(self, root, k):
res = []
self.dfs(root, res)
return res[k - 1]
def dfs(self, root, res):
if not root: return
self.dfs(root.left, res)
res.append(root.val)
self.dfs(root.right, res)
1 2 3 4 5 6 7 8 9 10 11
复杂度分析:
- 时间复杂度:O(N),因为每个节点只访问了一次;
- 空间复杂度:O(N),因为需要数组保存二叉树的每个节点值。
方法二:只保存第 k 个节点
在方法一中,我们保存了整个中序遍历数组,比较浪费空间。
其实我们只需要知道,在中序遍历的时候,第 k 个被访问的节点即可。访问到第 k 个节点后,递归终止,后面的节点就不用访问了。
下图展示了中序遍历过程中的节点访问顺序。
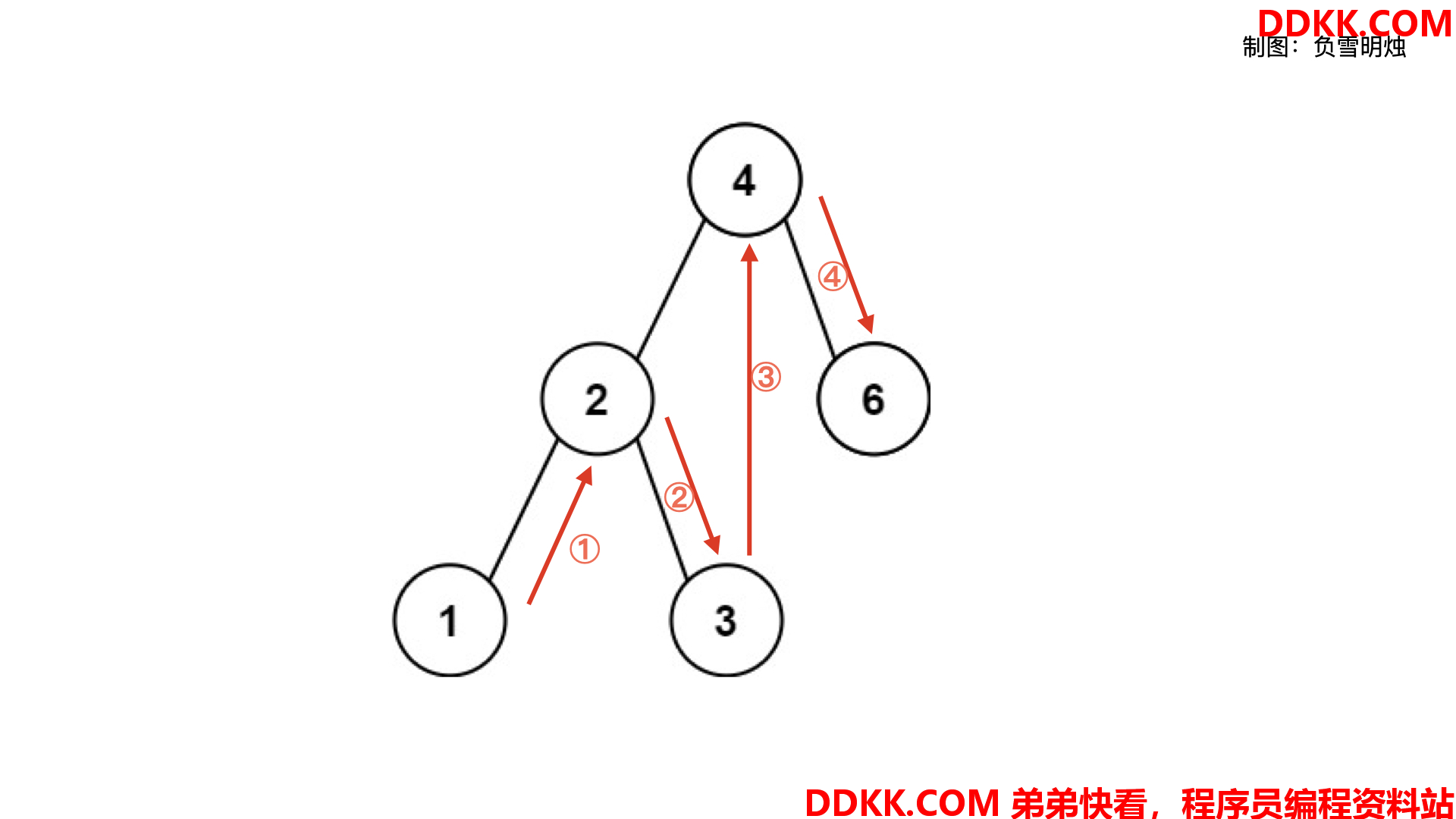
具体的做法中,我们需要需要两个变量:
1、 用一个全局变量保存最终的结果;
2、 用一个全局变量保存当前访问到第几个节点;
如果不使用全局变量,而是使用函数传参,需要注意「值传递」和「引用传递」的区别:
值传递:每个递归的内部都需要对同一个变量修改,如果用普通函数的传参,对于 int 型的参数,使用的是值传递,即拷贝了一份传到了函数里面。那么函数里面对 int 型的修改不会影响外边的变量。
使用全局变量,可以保证递归函数的每次修改都是反映到全局的,从而保证遍历到第 k 个的时候,所有的递归立刻停止。
Java 代码如下:
public class Solution {
int res;
int count;
public int kthSmallest(TreeNode root, int k) {
res = 0;
count = k;
dfs(root);
return res;
}
public void dfs(TreeNode root){
if(root == null){
return;
}
dfs(root.left);
count--;
if(count == 0){
res = root.val;
return;
}
dfs(root.right);
}
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
C++代码如下:
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
count = k;
dfs(root);
return res;
}
void dfs(TreeNode* root) {
if (!root) return;
dfs(root->left);
count -= 1;
if (count == 0) {
res = root->val;
return;
}
dfs(root->right);
}
private:
int res;
int count;
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Python 代码如下:
class Solution(object):
def kthSmallest(self, root, k):
self.res = 0
self.count = k
self.dfs(root)
return self.res
def dfs(self, root):
if not root: return
self.dfs(root.left)
self.count -= 1
if self.count == 0:
self.res = root.val
return
self.dfs(root.right)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
复杂度分析:
- 时间复杂度:O(k),因为只访问了前 k 个节点;
- 空间复杂度:O(h),其中 h 为树的高度,因为递归用了系统栈,而栈的深度最多只有树的高度。
迭代
待补。
总结
1、 二叉树的多种遍历方式必须要掌握;
2、 一定切记:二叉搜索树的中序遍历是有序的;
3、 另外建议刚开始刷题的朋友,不妨从二叉树上手;
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发