题目地址: https://leetcode.com/problems/maximal-square/description/
题目描述
Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
Example:
Input:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Output: 4
题目大意
给出了一个二维的数组,求在这里面能够成的最大的正方形面积是多少。
解题方法
动态规划
有两种方法,第一种就是对矩阵的每个位置求左上角以上所有元素的和,然后用所有可能构成的正方形的区域内进行面积计算,如果面积等于正方形边长的平方,说明是一个正方形,然后求最大面积。
第二种方法使用DP。设这个DP[i][j]数组为以i, j位置为右下角顶点的能够成的最大正方形的边长。数组如果是第一行或者第一列,显然dp和matrix相等。如果是其他位置,当matrix[i][j] = 1时,能够成的正方形等于左边、上边、左上能够成的正方形边长的最小值+1.为什么是最小值?因为只要存在一个0,那么就没法构成更大的正方形,这个是很保守的策略。
递推公式如下:
1、 dp[0][j]=matrix[0][j](topmostrow);;
2、 dp[i][0]=matrix[i][0](leftmostcolumn);;
3、 Fori>0andj>0:ifmatrix[i][j]=0,dp[i][j]=0;ifmatrix[i][j]=1,dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1.;
用图来说:
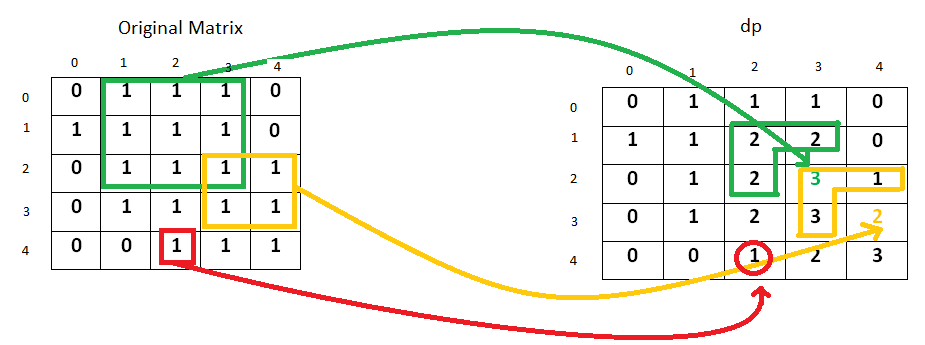
时间复杂度是O(N2),空间复杂度是O(N2)。
class Solution(object):
def maximalSquare(self, matrix):
"""
:type matrix: List[List[str]]
:rtype: int
"""
if not matrix: return 0
M = len(matrix)
N = len(matrix[0])
dp = [[0] * N for _ in range(M)]
for i in range(M):
dp[i][0] = int(matrix[i][0])
for j in range(N):
dp[0][j] = int(matrix[0][j])
for i in range(1, M):
for j in range(1, N):
if int(matrix[i][j]) == 1:
dp[i][j] = min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1
return max(map(max, dp)) ** 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
C++代码如下:
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
const int M = matrix.size(), N = matrix[0].size();
vector<vector<int>> dp(M, vector<int>(N, 0));
int res = 0;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (i == 0 || j == 0)
dp[i][j] = matrix[i][j] - '0';
else if (matrix[i][j] == '1')
dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
res = max(res, dp[i][j]);
}
}
return res * res;
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
参考资料:
https://leetcode.com/problems/maximal-square/discuss/61935/6-lines-Visual-Explanation-O(mn) https://www.youtube.com/watch?v=vkFUB--OYy0
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发