题目地址:https://leetcode.com/problems/smallest-range-i/description/
题目描述
Given an array A of integers, for each integer A[i] we may choose any x with -K <= x <= K, and add x to A[i].
After this process, we have some array B.
Return the smallest possible difference between the maximum value of B and the minimum value of B.
Example 1:
Input: A = [1], K = 0
Output: 0
Explanation: B = [1]
Example 2:
Input: A = [0,10], K = 2
Output: 6
Explanation: B = [2,8]
Example 3:
Input: A = [1,3,6], K = 3
Output: 0
Explanation: B = [3,3,3] or B = [4,4,4]
Note:
1、 1<=A.length<=10000;
2、 0<=A[i]<=10000;
3、 0<=K<=10000;
题目大意
经常看我题解的同学都知道,我每次都上来先分析题目意思,这是做对题的第一步。
本题是说对于数组中的每个元素,都可以对其值进行修改:加上 [-k, k] 内的任意整数。问如何对整个数组修改后,数组的最大值减去最小值的差,是最小的。
举个例子,假如输入数组是 [3,6],k=2。
那么对于 3 来说,可以变成 [1,2,3,4,5] 中的一个:
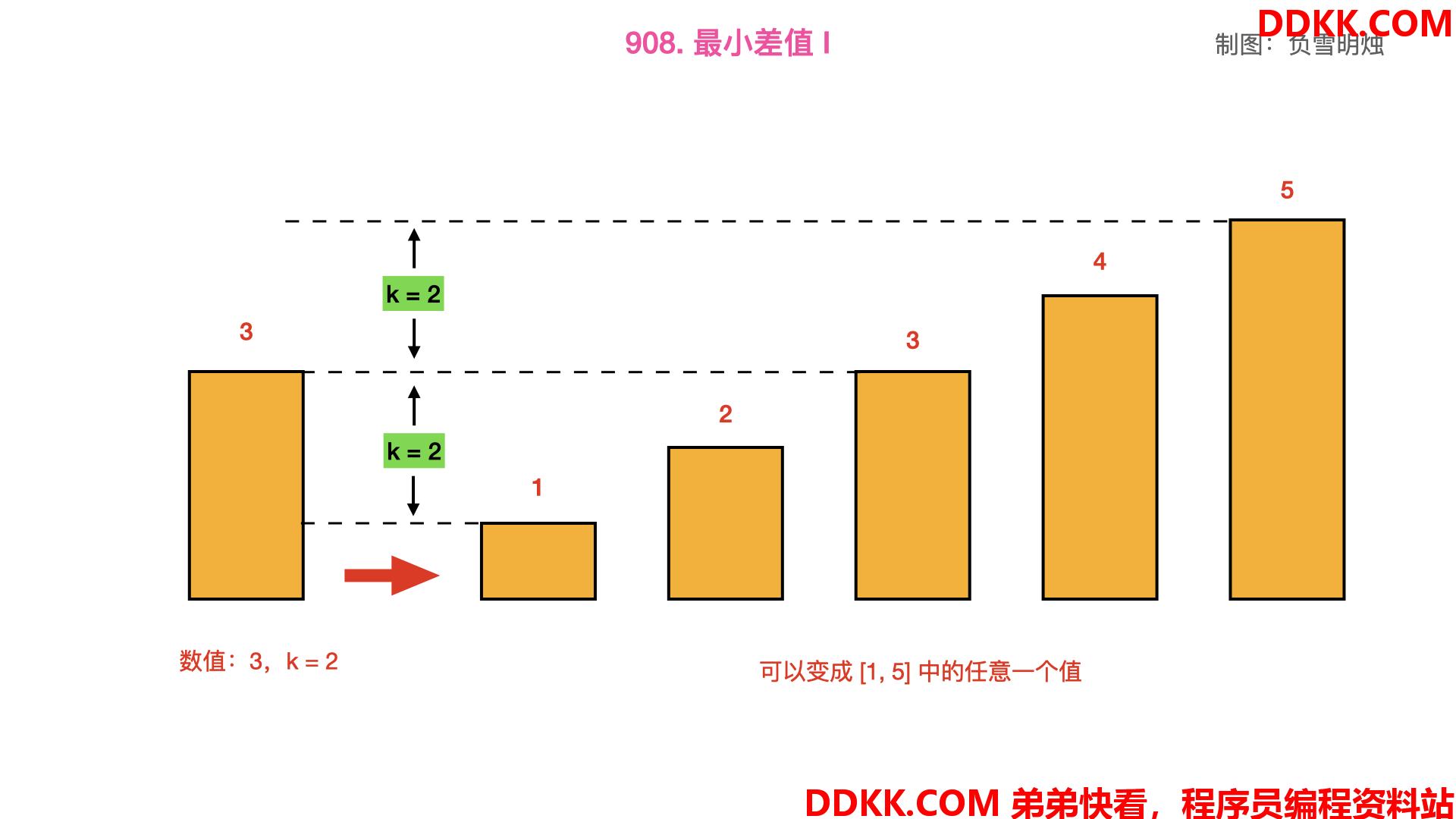
那么对于 6 来说,可以变成 [4,5,6,7,8] 中的一个:
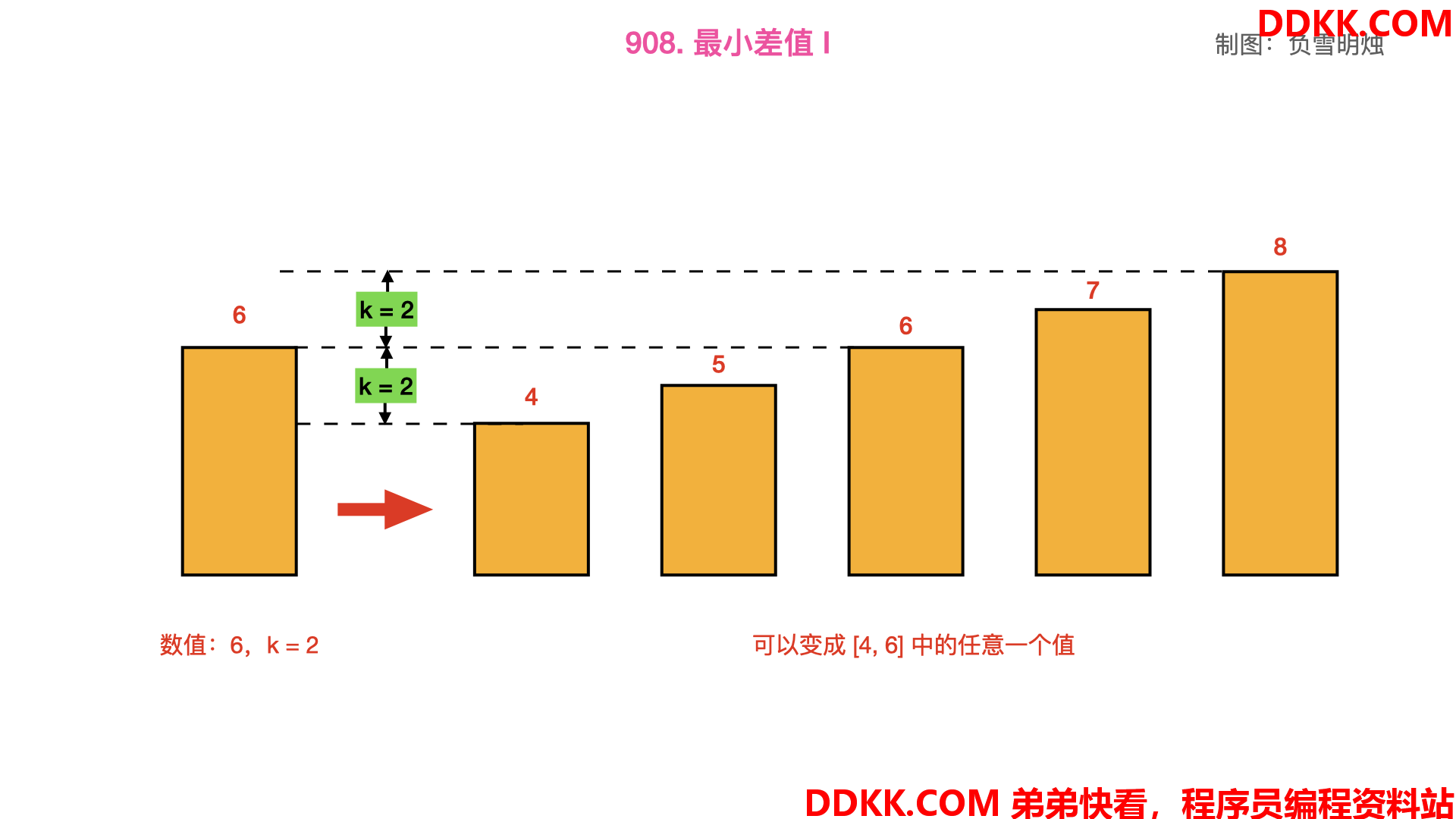
因此,可以把数组 [3,6] 变成 [4,4] 或者 [5,5],此时的最大值和最小值相等,即差值为 0。
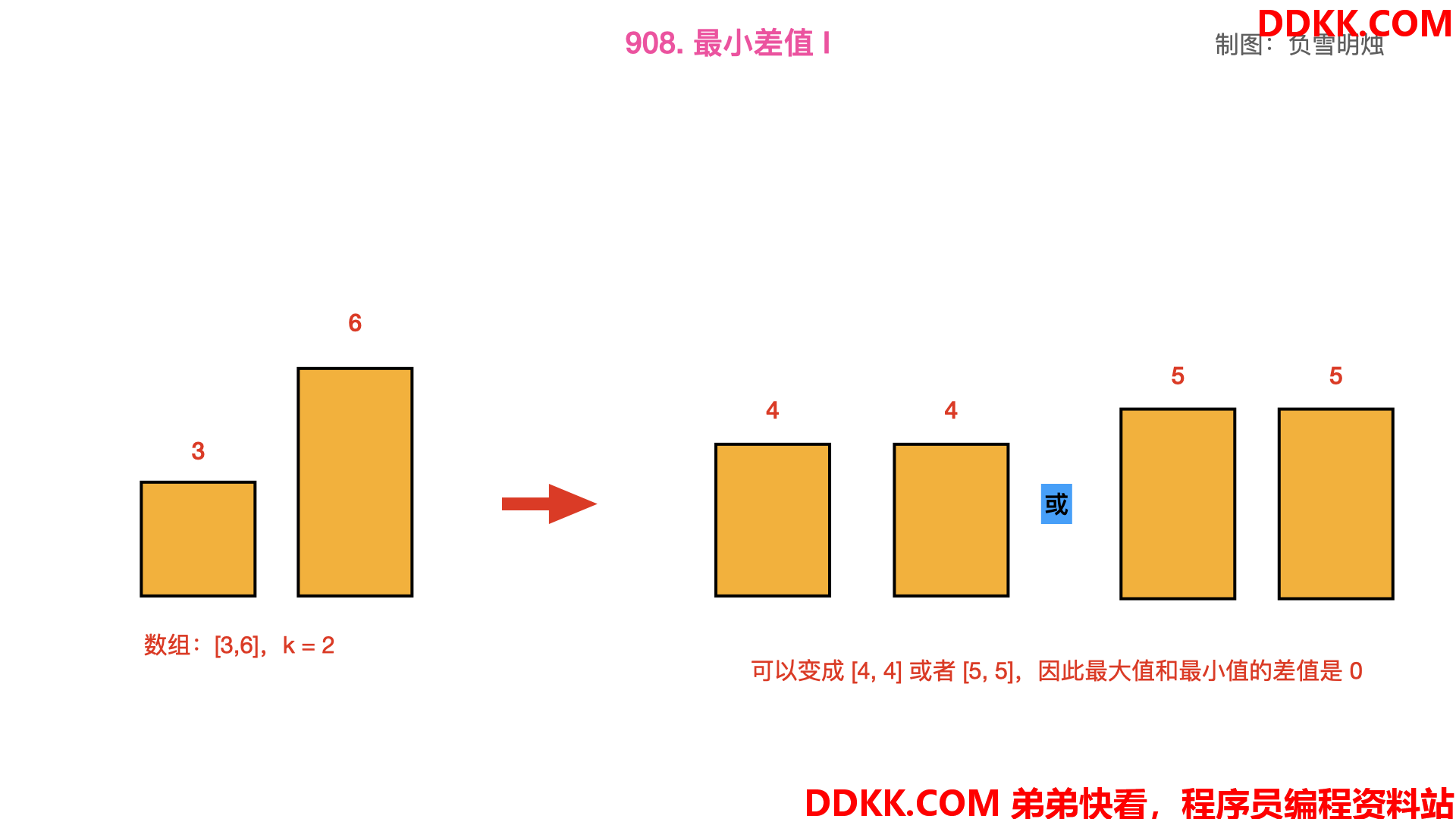
解题方法
对于本题,我的第一想法是把最小值 + k,最大值 - k,修改后的数组最大值与最小值的差 “应该是” 最小的。
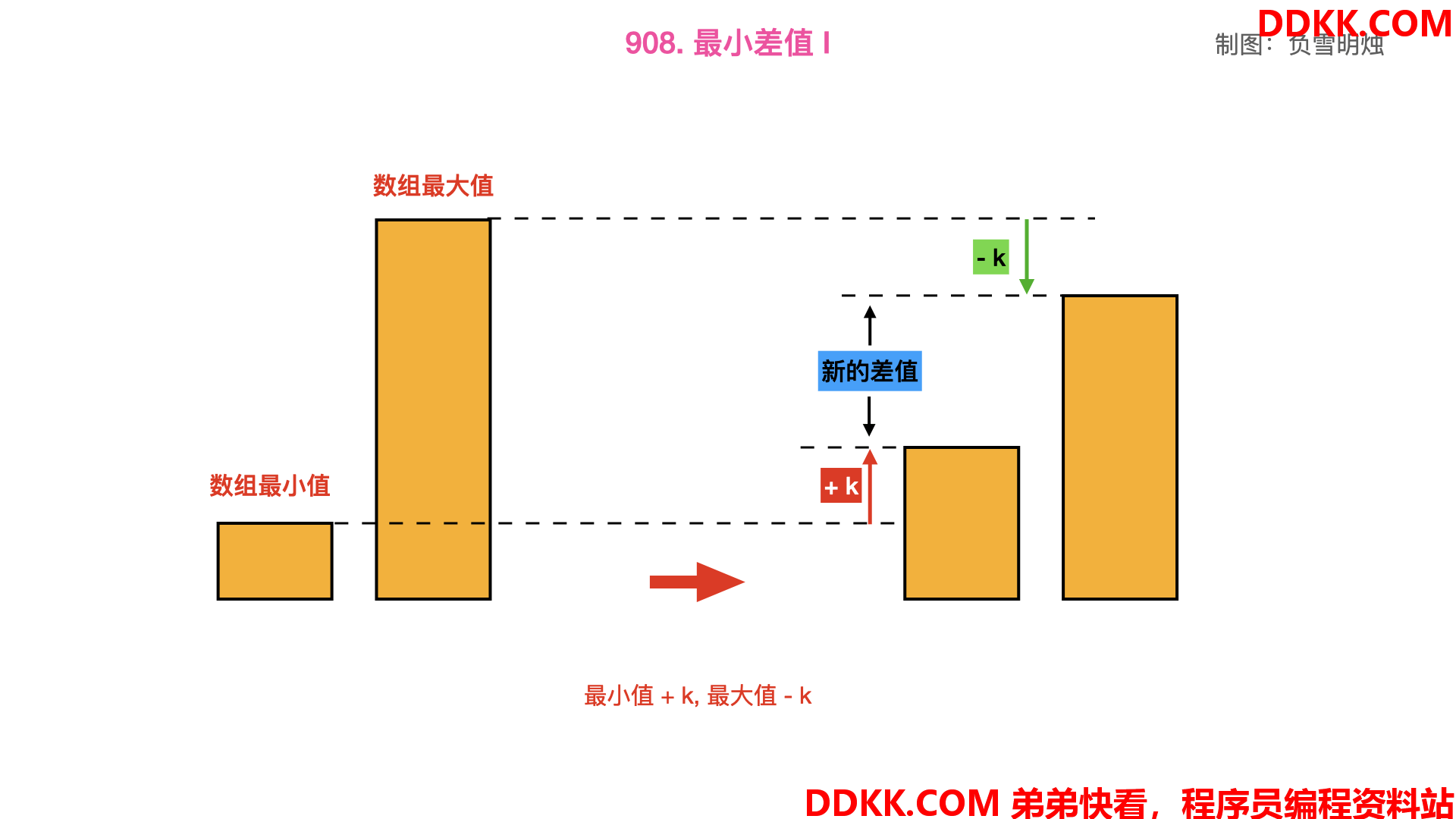
转念一想,不对啊!假如 最小值 + k > 最大值 - k,经过上面的转化,矮的变成高的了、高的变成矮的了。其实本来差值可以变成 0 的,但是却导致「矫枉过正」了。
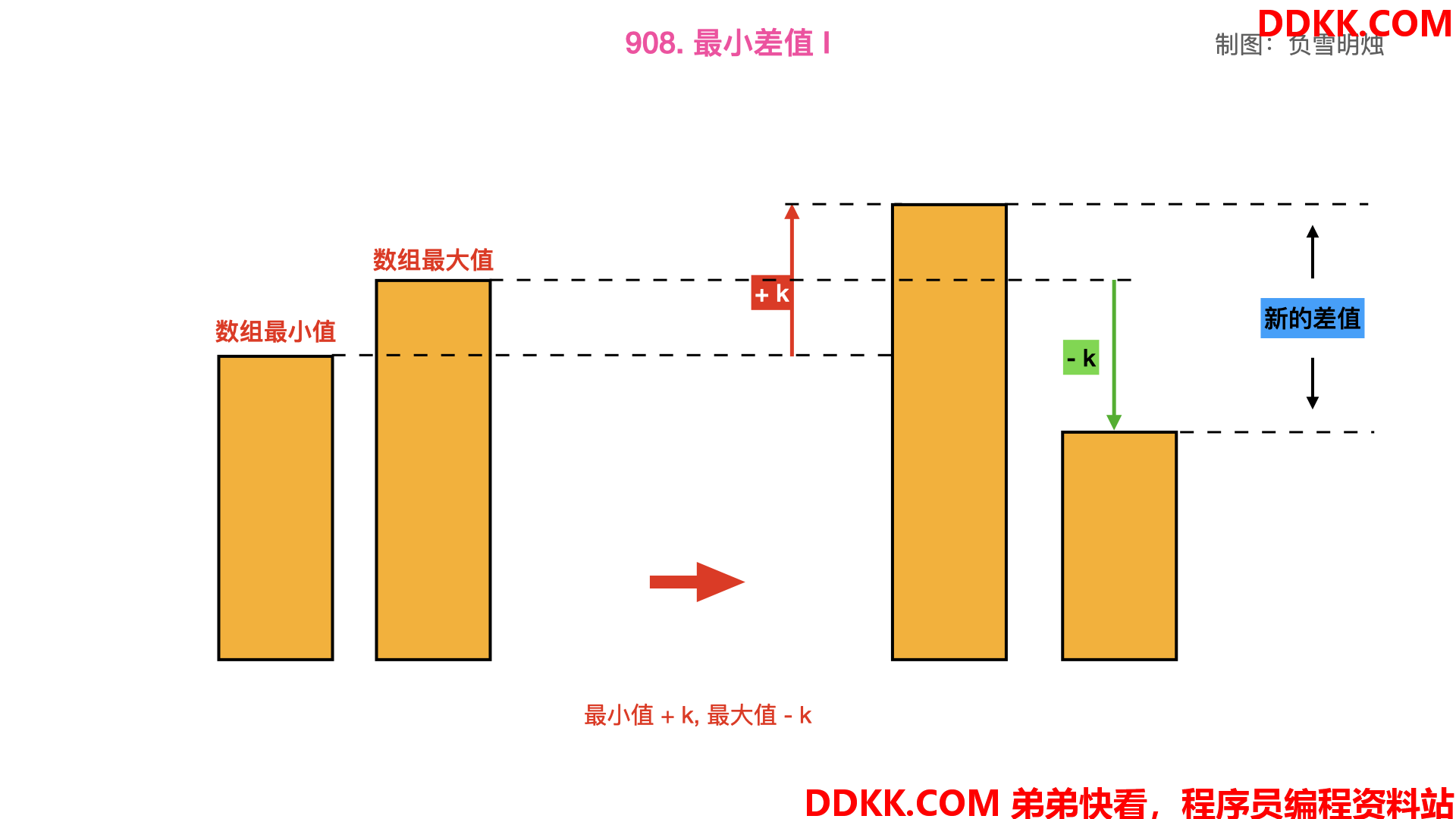
因此,需要多加个判断,思路也就有了:
- 当原数组的最大值 - 最小值 >` 2 * k,那么把最小值 + k,最大值 - k,得到的新数组的最大值和最小值的差最小。
- 否则,得到的新数组的最大值和最小值的差就是 0。(不要「矫枉过正」)
代码如下:
class Solution(object):
def smallestRangeI(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
diff = max(nums) - min(nums)
if diff > 2 * k:
return diff - 2 * k
return 0
1 2 3 4 5 6 7 8 9 10 11
或者换一种写法:
class Solution(object):
def smallestRangeI(self, A, K):
"""
:type A: List[int]
:type K: int
:rtype: int
"""
return max(max(A) - min(A) - 2 * K, 0)
1 2 3 4 5 6 7 8
复杂度
- 时间复杂度:O(N)
- 空间复杂度:O(1)
总结
1、 对于这种题目,并不需要真正的把“新数组”的每个值都计算出来,只需要求出一个值来,那么一般就是靠思路和规律取胜,不要暴力求“新数组”哦~;
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发