有向无环图及其应用
一个无环的有向图称做有向无环图,简称DAG图。
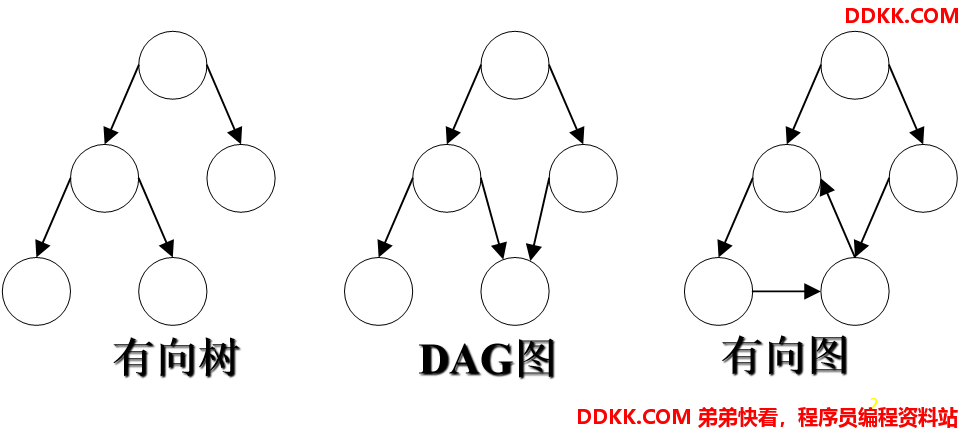
DAG图是一类较有向树更一般的特殊有向图。
拓扑排序
通常我们把计划、施工过程、生产流程、程序流程等都当成一个工程,一个大的工程常常被划分成许多较小的子工程,这些子工程称为活动。这些活动完成时,整个工程也就完成了。
例,计算机专业学生的课程开设可看成是一个工程,每一门课程就是工程中的活动。
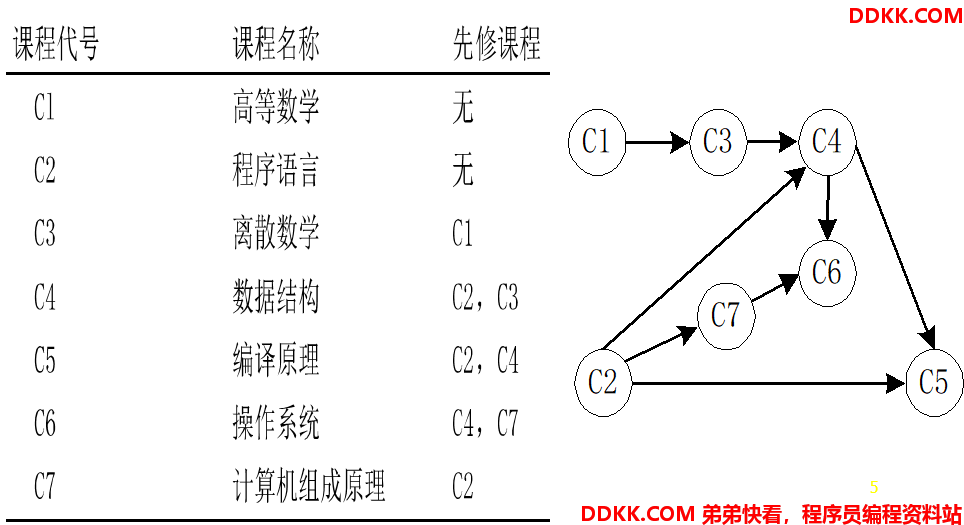
顶点表示活动,有向边表示活动的先后关系的网简称为AOV网。
AOV网中不能有环,否则工程无法顺利进行。
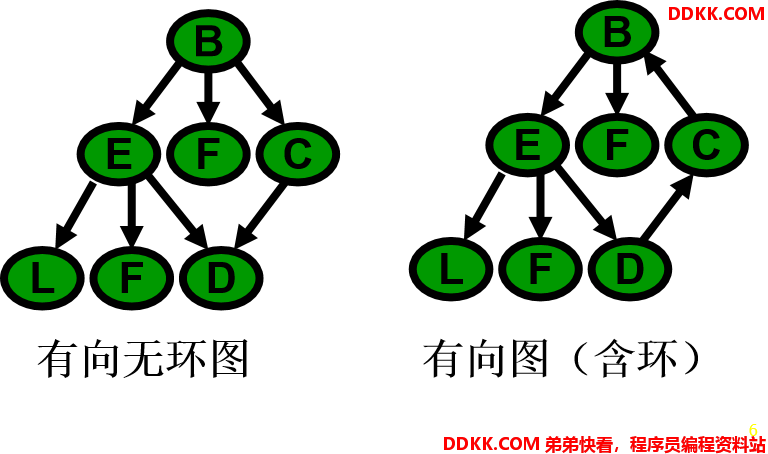
在AOV网中,若不存在回路,则所有活动可排成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列(Topological Order),由AOV网构造拓扑序列的过程叫做拓扑排序 (Topological Sort)。
如何进行拓扑排序?
对AOV网进行拓扑排序的方法是:
①在AOV网中选择一个入度为0的顶点,并输出它到拓扑序列中;
②从网中删去该顶点及它的所有出边;
反复执行①②两步,直到网中所有顶点都被输出了(拓扑序列完成),或网的剩余部分中再也选不出入度为0的顶点(图中有环)为止。
例:对下列AOV网进行拓扑排序。
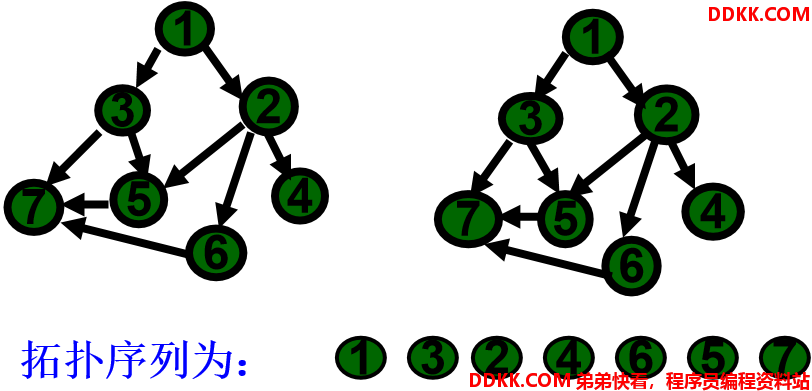
拓扑排序算法(邻接矩阵)
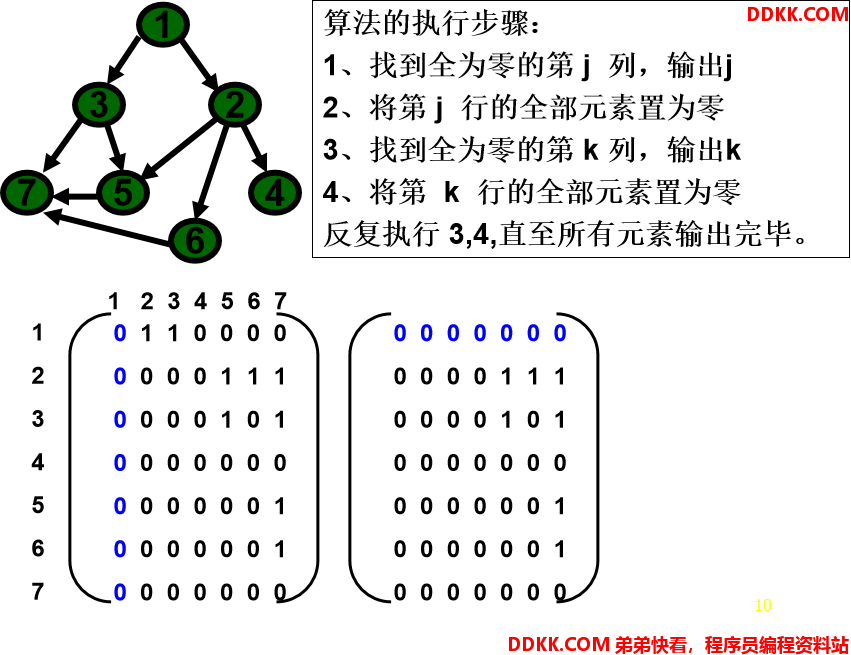
AOE网与关键路径
一、AOE网概念
1、 定义若在带权的有向图中,以顶点表示事件,有向边表示活动,边上的权值表示完成该活动的开销(如该活动所需的时间),则称此带权的有向图为用边表示活动的网络,简称AOE网(ActivityOnEdge);
2、 说明(1)AOV网与AOE网有密切关系又有不同如果用他们表示工程,AOV网表示各个子工程之间的优先关系,是定性关系;在AOE网中还要体现完成各个子工程的确切时间,是定量关系;
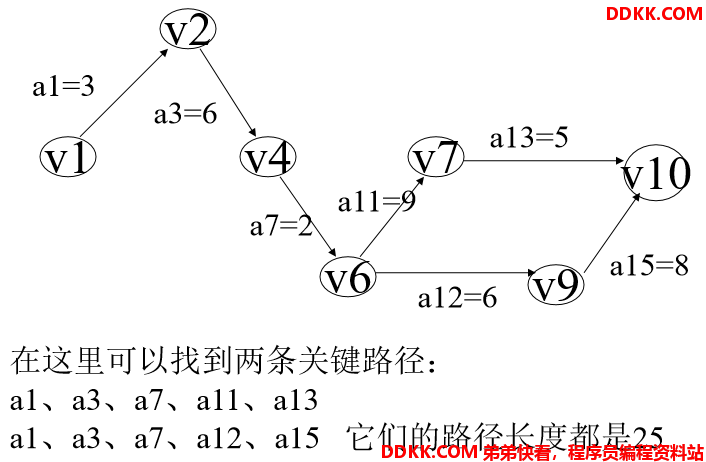
整个工程完成的时间为:从有向图的源点到汇点的最长路径。
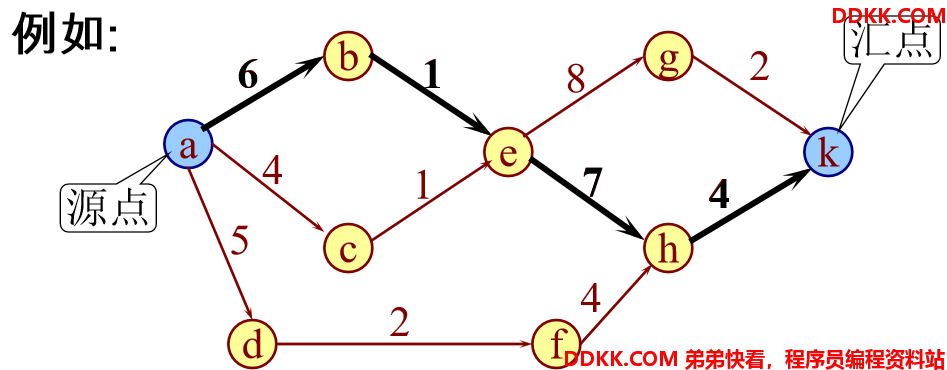
“关键活动”指的是:该弧上的权值增加 将使有向图上的最长路径的长度增加。
对于AOE网,我们关心的问题是:
(A)完成整个工程至少需要多少时间?
(B)哪些活动是关键活动:哪些活动的进度是影响整个工程进度的关键?
2、 在AOE网中,只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始。只有在进入每顶点的各有向边所代表的活动都已经结束后,该顶点所代表的事件才能发生。
3、 在一个表示工程的AOE网中,应该不存在回路,网中仅存在一个入度为零的顶点,乘作开始顶点,它表示了整个工程的开始;网中仅存在一个出度为零的顶点,称为结束顶点,它表示整个工程的结束。
二、关键路径有关术语
1、 路径长度;
AOE网中一条路径的长度是该路径上个活动所需时间的总和。
2、 关键路径;
AOE网中,从开始顶点到结束顶点之间路径长度中的最大路径为关键路径。由于AOE网中某些子工程(活动)可以同时进行,要保证每个子工程都能完成,完成该工程的最少时间就是该工程AOE网的关键路径长度。
3、 事件的最早发生时间;
事件vi的最早发生时间ve(i)是从开始顶点v到vi的最长路径长度。
4、 活动的最早开始时间;
活动aj的最早开始时间e (j)是该活动的起点所表示的事件最早发生时间,如果由边(vi,vk)表示活动aj,则有e(j)=ve(i)。
5、 事件的最迟发生时间;
事件vk的最迟发生时间vl(k)是在不推迟整个工程完成(即保证结束顶点vn在ve(n)时刻发生)的前提下,该事件最迟必须发生的时间。vl(k)为ve(n)减去顶点vk到结束顶点vn的最长路径的长度.
6、 活动的最迟开始时间;
活动aj的最迟开始时间l(j)是该活动的终点所表示的事件最迟发生时间与该活动的所需时间之差。如果由边(vi,vk)表示活动aj,则有 l(j)=vl(k)-aj所需时间.
7、 时间余量;
活动aj的 l(j)-e(j)是该活动完成的时间余量。它是在不增加完成整个工程所需时间的情况下,活动aj可以拖延的时间。
8、 关键活动;
当一活动的时间余量=0,说明该活动必须如期完成,否则就会拖延完成整个工程的进度。若活动aj的时间余量=0,则称该活动为关键活动。当时间余量>0,活动aj不是关键活动,只要拖延的时间不超过时间余量,就不会影响整个工程的进度;但如果拖延的时间超过时间余量,则关键活动就可能发生变化。
一、计算事件的最早发生时间ve(k)

二、计算事件的最迟发生时间vl(k)

三、计算活动ai的最早开始时间e[i] 若活动ai有边<vj,vk>表示,则活动ai的最早开始时间e[i]可由下式计算: e[i]=ve[j]
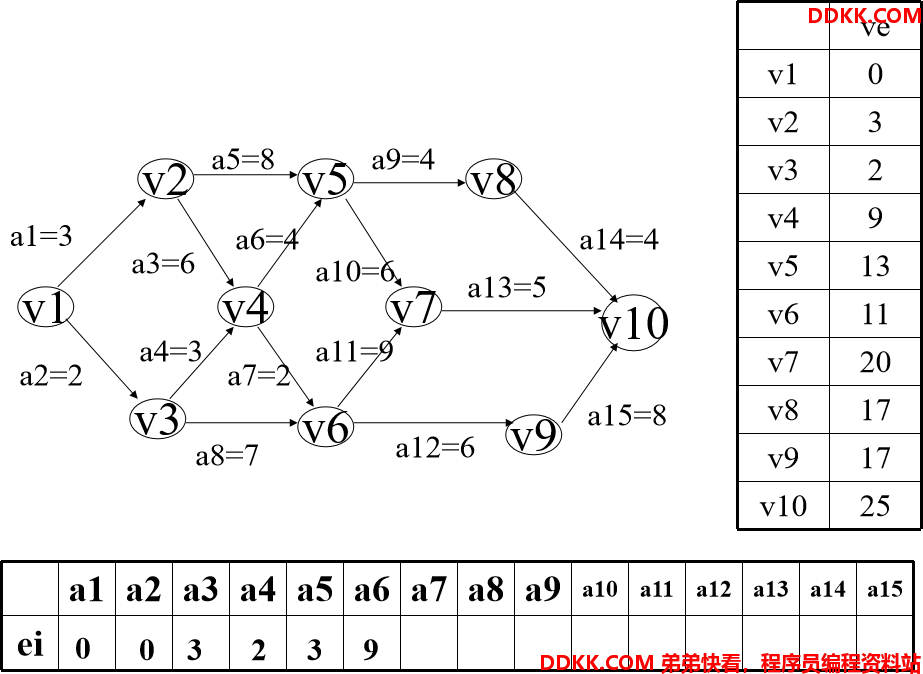
四、计算活动ai的最迟开始时间l[i] 若活动ai有边<vj,vk>表示,则活动ai的最迟开始时间l[i]可由下式计算: l[i]=vl[k]-<vj,vk>
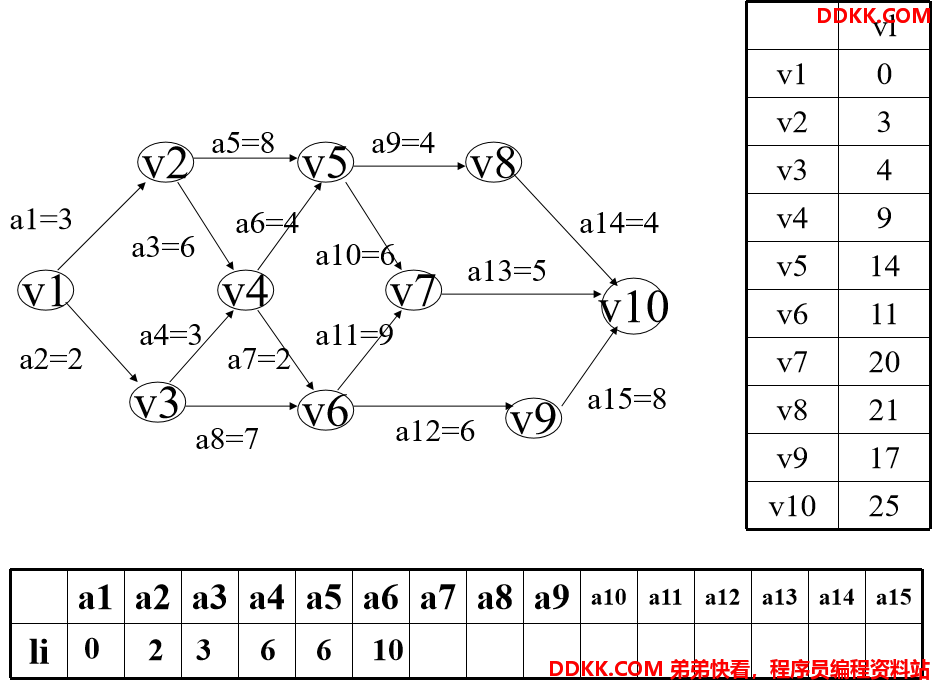
五、计算活动ai的时间余量d[i]确定关键路径 令d[i]=l[i]-e[i],对于活动ai,若有d[i]=0,则说明活动ai为关键活动,由关键活动组成的路径就是关键路径。
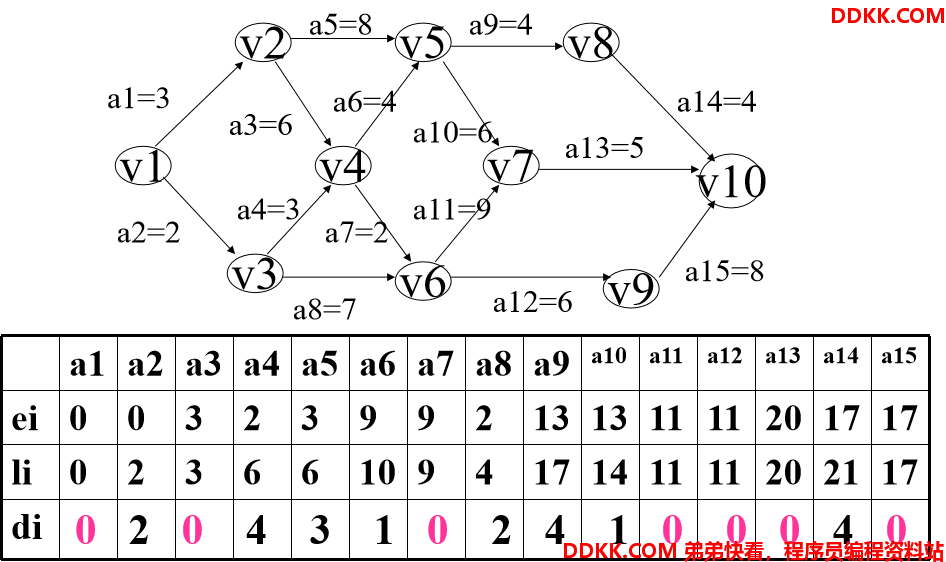
对于AOE网,我们所关心的有两个问题:
1、 完成整个工程的时间可由ee[n]求得;
2、 关键活动(哪些活动的进度是影响整个工程进度的关键);