二叉排序树(Binary Sort Tree)又称为二叉查找树(Binary Search Tree)、二叉搜索树。
它是特殊的二叉树:
对于二叉树,假设x为二叉树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。 如果y是x的左子树中的一个结点, 则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]。那么,这棵树就是二叉查找树。
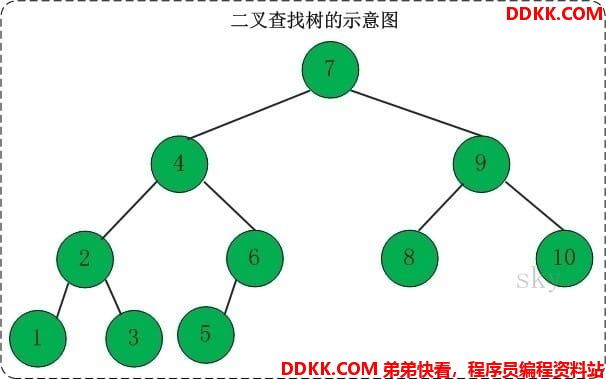
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后再就行和每个节点的父节点比较大小,查找最合适的范围。这个算法的效率查找效率很高,但是如果使用这种查找方法要首先创建树。
它或者是一颗空树,或者是具有下列性质的二叉树:
1、 若任意节点的左子树不为空,则左子树上的所有节点的值均小于它的根结点的值;
2、 若任意节点的右子树不为空,则右子树上所有节点的值均大于它的根结点的值;
3、 任意节点的左、右子树也分别为二叉查找树;
4、 没有键值相等的节点;
二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。
构造一颗二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。不管怎么说,在一个有序数据集上的查找,速度总是要快于无序的数据集的,而二叉排序树这样的非线性结构,也有利于插入和排序的实现。
二叉查找树的高度决定了二叉查找树的查找效率。
查找
在二叉查找树中查找x的过程如下:
1、 若二叉树是空树,则查找失败;
2、 若x等于根结点的数据,则查找成功,否则;
3、 若x小于根结点的数据,则递归查找其左子树,否则;
4、 递归查找其右子树;
复杂度分析,它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
根据上述的步骤,写出其查找操作的代码:
c语言实现:


/*二叉树的查找,非递归*/
BiSTNode *BST_Search1(BiSTree t, KeyType kx , BiSTNode **parent)
{ /*在二叉排序树t上查找关键字为kx的元素,若找到,返回所在结点的地址,否则返回空指针,通过形参parent返回待查找结点kx的父结点地址*/
BiSTNode *p = t, *q = NULL;
while(p) { /*从根结点开始查找*/
if (kx == p->data.key) { /*查找成功*/
*parent = q;
return(p);
}
q = p;
if(kx < p->data.key)
p = p->lchild; /*kx小于p的关键字,在左子树查找*/
else
p = p->rchild; /*kx大于p的关键字,在右子树查找*/
}
*parent = q;
return p; /*查找失败*/
}
View Code


/*二叉树的查找,递归算法*/
BiSTNode *BST_Search2 (BiSTree t, KeyType kx)
{ /*在二叉排序树t上查找关键字为kx的元素,若找到,返回所在结点的地址,否则返回空指针*/
if (t == NULL || t->data.key == kx)
return(t); /*若树空或根结点等于kx*/
else if(kx < t ->data.key)
BST_Search2(t->lchild, kx);
else
BST_Search2(t->rchild, kx);
}
View Code
Java实现:


public boolean contains(T t)
{
return contains(t, rootTree);
}
/**从某个结点出开始查找元素*/
public boolean contains(T t, BinaryNode<T> node)
{
if(node==null)
return false;//结点为空,查找失败
int result = t.compareTo(node.data);
if(result>0)
return contains(t,node.right);//递归查询右子树
else if(result<0)
return contains(t, node.left);//递归查询左子树
else
return true;
}
/**
这里我提供一个对二叉树最大值
最小值的搜索*/
/**找到二叉查找树中的最小值*/
public T findMin()
{
if(isEmpty())
{
System.out.println("二叉树为空");
return null;
}else
return findMin(rootTree).data;
}
/**找到二叉查找树中的最大值*/
public T findMax()
{
if(isEmpty())
{
System.out.println("二叉树为空");
return null;
}else
return findMax(rootTree).data;
}
/**查询出最小元素所在的结点*/
public BinaryNode<T> findMin(BinaryNode<T> node)
{
if(node==null)
return null;
else if(node.left==null)
return node;
return findMin(node.left);//递归查找
}
/**查询出最大元素所在的结点*/
public BinaryNode<T> findMax(BinaryNode<T> node)
{
if(node!=null)
{
while(node.right!=null)
node=node.right;
}
return node;
}
View Code
插入
插入:从根结点开始逐个与关键字进行对比,小了去左边,大了去右边,碰到子树为空的情况就将新的节点连接。二叉查找树的插入过程如下:
-
- 若当前的二叉查找树为空,则插入的元素为根节点;
-
- 若插入的元素值小于根节点值,则将元素插入到左子树中;
-
- 若插入的元素值不小于根节点值,则将元素插入到右子树中。
c语言实现:


BiSTree BST_InsertNode (BiSTree t, KeyType kx)
{ /*在二叉排序树上插入关键字为kx的结点*/
BiSTNode *f, *p, *s;
p = t;
while(p) { /*寻找插入位置*/
if (kx == p->data.key) {
printf("kx已存在,不需插入");
return(t);
} else {
f = p; /*结点f指向结点p的双亲*/
if(kx < p->data.key)
p = p->lchild;
else
p = p->rchild;
}
}
s = ( BiSTNode *)malloc(sizeof(BiSTNode)); /*申请并填装结点*/
s->data.key = kx; s->lchild = NULL; s->rchild = NULL;
if (!t) t = s; /*向空树中插入时*/
else if(kx < f->data.key)
f->lchild = s; /*插入结点s为结点f的右孩子*/
else
f->rchild = s; /*插入结点s为结点f的左孩子*/
return(t);
}
View Code
Java实现:


/**插入元素*/
public void insert(T t)
{
rootTree = insert(t, rootTree);
}
/**在某个位置开始判断插入元素*/
public BinaryNode<T> insert(T t,BinaryNode<T> node)
{
if(node==null)
{
//新构造一个二叉查找树
return new BinaryNode<T>(t, null, null);
}
int result = t.compareTo(node.data);
if(result<0)
node.left= insert(t,node.left);
else if(result>0)
node.right= insert(t,node.right);
else
;//doNothing
return node;
}
View Code
删除
如果要删除的节点是叶子,直接删;如果只有左子树或只有右子树,则删除节点后,将子树连接到父节点即可;如果同时有左右子树,则可以将二叉排序树进行中序遍历,取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。
二叉查找树的删除,分三种情况进行处理:
-
- p为叶子节点,直接删除该节点,即修改其父节点的指针(注意分是根节点和不是根节点),如图a;
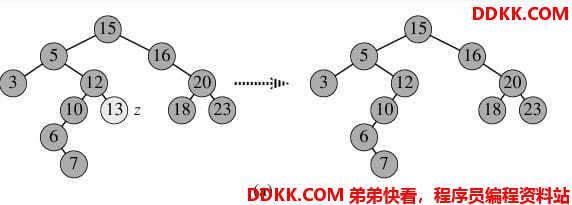
- p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可(注意分是根节点和不是根节点),如图b;
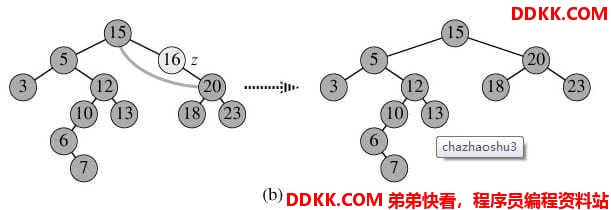
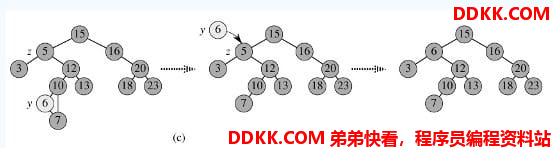
- p的左子树和右子树均不空。即待删除的结点同时有左子树和右子树。根据二叉树的特点,可以从其左子树选择关键字最大的结点或右子树关键字最小的结点放在被删去结点的位置上。如图c,删除5。
/**删除元素*/
public void remove(T t)
{
rootTree = remove(t,rootTree);
} /**在某个位置开始判断删除某个结点*/
public BinaryNode<T> remove(T t,BinaryNode<T> node)
{
if(node == null)
return node;//没有找到,doNothing
int result = t.compareTo(node.data);
if(result>0)
node.right = remove(t,node.right);
else if(result<0)
node.left = remove(t,node.left);
else if(node.left!=null&&node.right!=null)
{
node.data = findMin(node.right).data;
node.right = remove(node.data,node.right);
}
else
node = (node.left!=null)?node.left:node.right;
return node;
}
二叉排序树的查找分析
1)二叉排序树上查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径。
比较的关键字次数=此结点的层次数;
最多的比较次数=树的深度(或高度),即 log2 n+1
2)一棵二叉排序树的平均查找长度为:
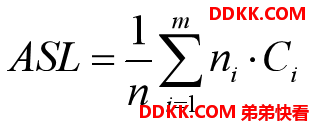
其中:ni 是每层结点个数; Ci 是结点所在层次数; m 为树深。
最坏情况:即插入的n个元素从一开始就有序, ——变成单支树的形态! 此时树的深度为n ; ASL= (n+1)/2 此时查找效率与顺序查找情况相同。
最好情况:即:与折半查找中的判定树相同(形态比较均衡)
树的深度为:log 2n +1 ; ASL=log 2(n+1) –1 ;与折半查找相同。