图的基本概念
图是由一个顶点集 V 和一个边集 E构成的数据结构。Graph=(V,E)
图中代表一条边的顶点的偶对如果无方向性,即无序,则称此图为无向图。
例:
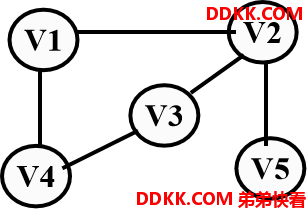
V={V1,V2,V3,V4,V5};
E={(V1,V2),(V1,V4), (V2,V3),(V3,V4), (V2,V5)}
在无向图中,(x, y)与(y, x)表示同一条边。
图中代表一条边的顶点的偶对如果有序的,则称此图为有向图。在有向图中,用<x, y>表示一条有向边,在有向图中也称边为“弧”,x称为边的弧尾或始点,称此边为顶点x 的一条出边;y称为边的弧头或终点,称此边为顶点y 的一条入边。
例:
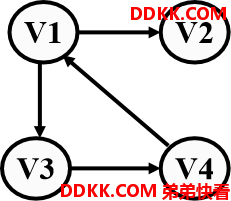
V={V1,V2,V3,V4};
E={<V1,V2>,<V1,V3>,<V3,V4>,<V4,V1>}
有向图中<x,y>与<y,x>是方向相反的两条弧。
顶点的度
一个顶点V的度是和顶点V关联的边的数目,记作D(V)。 在有向图中,一个顶点依附的弧头数目,称为该顶点的入度,记作ID(V)。一个顶点依附的弧尾数目,称为该顶点的出度,记作OD(V)。 某个顶点的入度和出度之和称为该顶点的度,即D(V)=ID(V)+OD(V)。
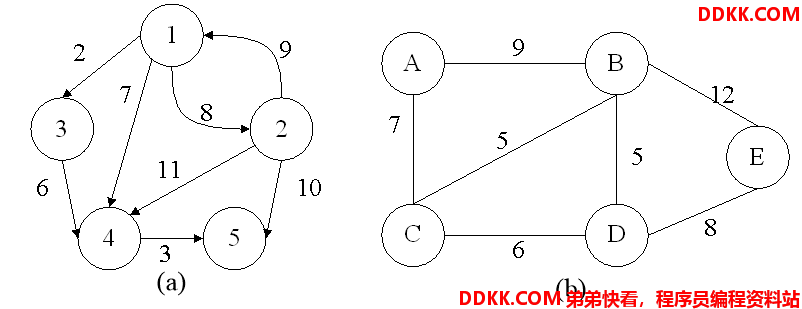
网(带权图)
在一个图中,每条边或弧可以标上具有某种含义的数值,此数值称为该边的权(weight)。弧或边带权的图分别称作有向网或无向网****。
图的存储结构
邻接矩阵
邻接矩阵是表示顶点之间相邻关系的矩阵。设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵。
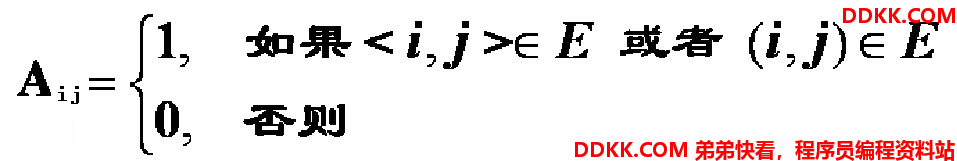
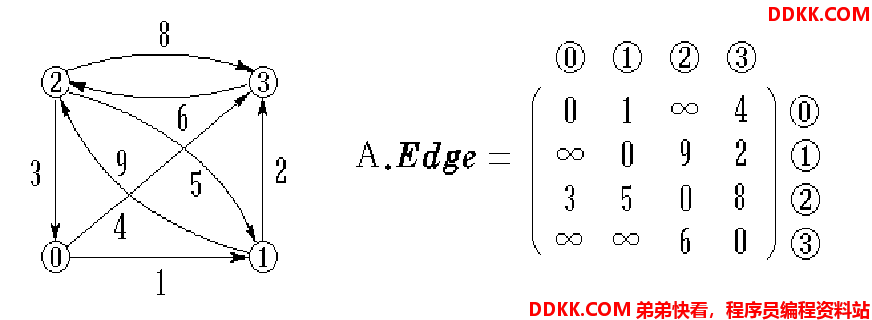
无向图的邻接矩阵是对称的,有向图的邻接矩阵不一定是对称的。
例如(网的邻接矩阵):

c语言实现:
typedef int VertexType; /*图中结点的数据类型为整型*/
typedef struct
{
VertexType v[MAX_VERTEX_NUM]; /*顶点表*/
int A[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*邻接矩阵*/
int vexnum,arcnum; /*图的顶点数和弧数*/
}MGraph;
邻接矩阵法优点:
容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
邻接矩阵法缺点:
n个顶点需要n*n个单元存储边(弧);空间效率为O(n2)。 对稀疏图而言尤其浪费空间。
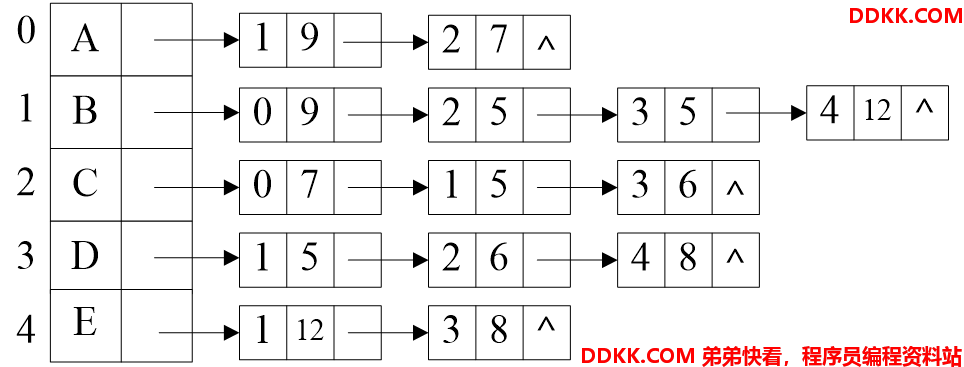
邻接表
邻接表是图的一种链式存储结构。类似于树的孩子链表表示法。
1)为每个顶点建立一个单链表,
2)第i个单链表中包含顶点Vi的所有邻接顶点。
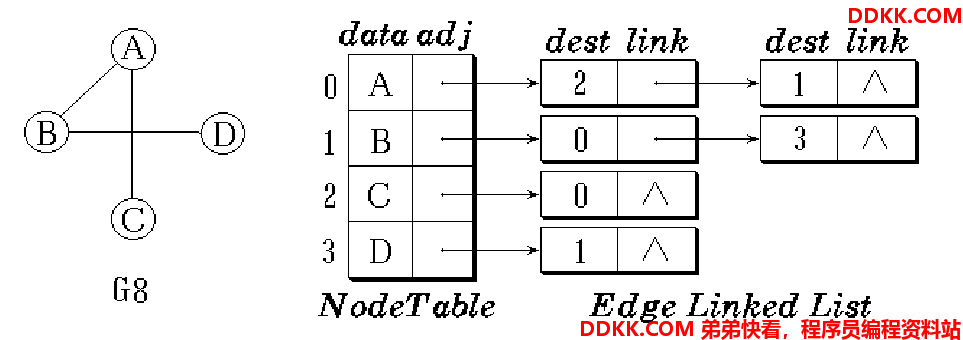
例如
无向图的邻接表:
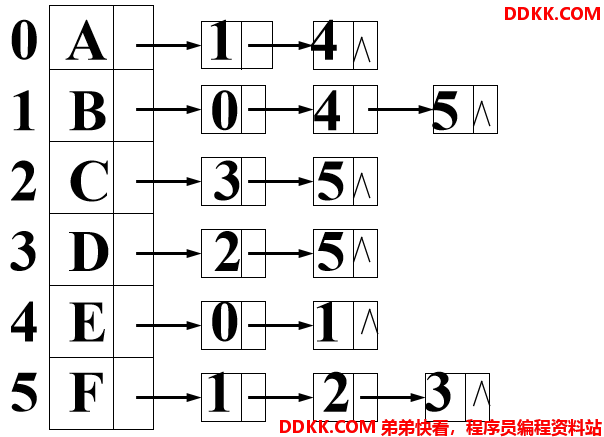
无向图中邻接表所有边结点的度数总和等于边数的2倍。
有向图的邻接表
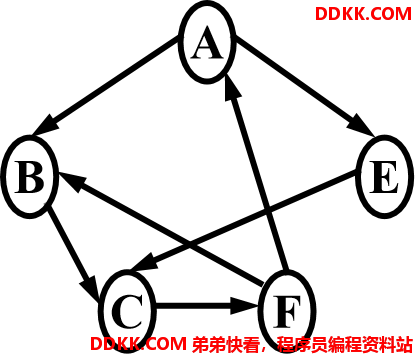
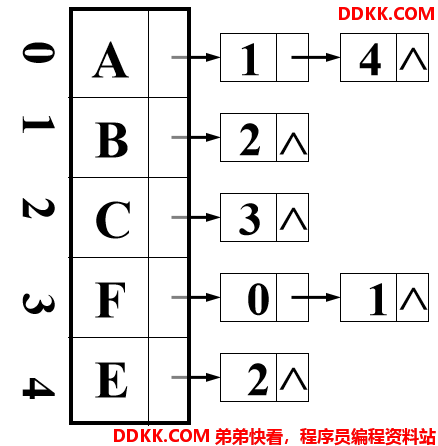
在有向图的邻接表中,链接的是每个结点的出边。
在有向图的邻接表中,第i个链表中边结点的个数是顶点Vi的出度;但不容易计算该顶点的入度。
有向图的逆邻接表
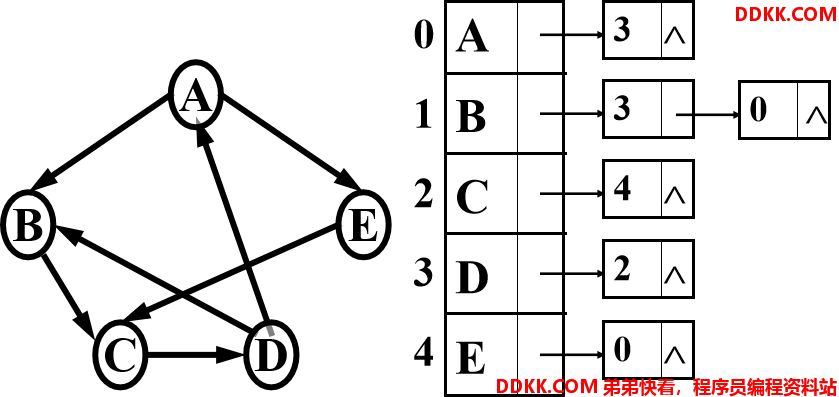
有向图的逆邻接表中,连接的是每个结点的入边。
在有向图的逆邻接表中,第i个链表中边结点的个数是顶点Vi的入度。
有向图的邻接表(或逆邻接表)中所有边结点的个数总和等于边数。
带权图的邻接表存储形式
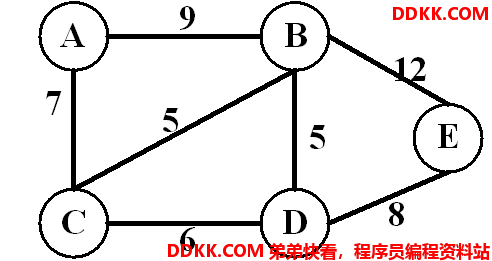
邻接表c语言实现
/*边结点结构*/
typedef struct ArcNode {
int adjvex; /*该弧所指向的顶点的位置*/
struct ArcNode *nextarc; /*下一条弧*/
//InfoType info; /*该弧上的权值*/
} ArcNode;
/*顶点的结点结构*/
typedef int VertexType;
typedef struct VNode {
VertexType data;
ArcNode *firstarc; //边表头指针
}VNode;
typedef struct {
VNode vertices[MAX_VERTEX_NUM];
int vexnum, arcnum; /*图的顶点数和弧数*/
}ALGraph;
邻接表的优点:
空间效率高;容易寻找顶点的邻接点;
邻接表的缺点:
判断两顶点间是否有边或弧,需搜索两结点对应的单链表,没有邻接矩阵方便。
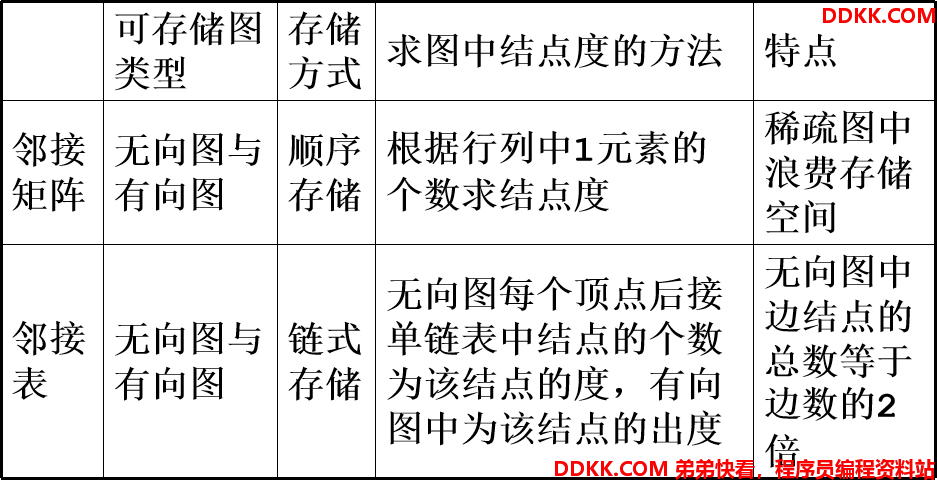
图的两种存储方式比较