二叉树
定义
二叉树(Binary Tree)是n个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两棵互不相交的分别成为左子树和右子树的二叉树组成。
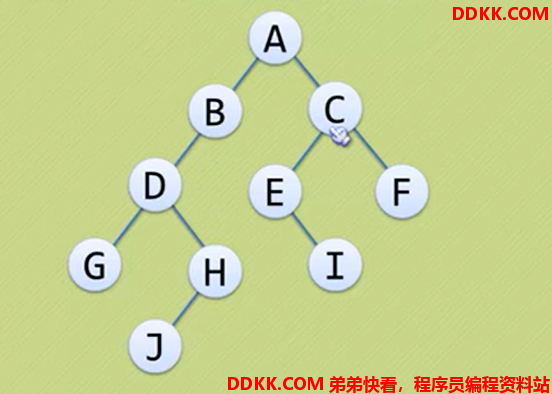
特点
1、 每个结点最多有两棵子树,所以不存在度大于2的结点;
2、 左子树和右子树是有顺序的,次序不能颠倒;
3、 即使树中某结点只有一颗子树,也要区分是左子树还是右子树;

基本形态
1、 空二叉树;
2、 只有一个根结点;
3、 根结点只有左子树;
4、 根结点只有右子树;
5、 根结点左右子树都有;
单层的二叉树
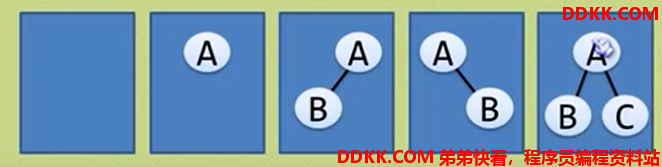
二层的
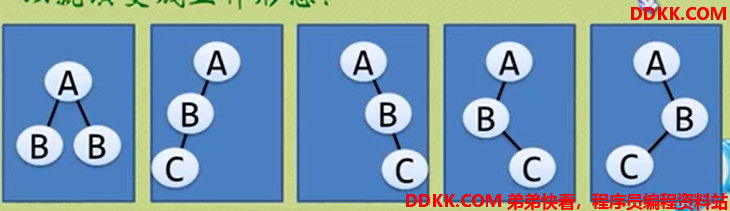
特殊二叉树
斜树
斜树:一定要是斜的(沿着同一个方向)
满二叉树
满二叉树:所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上。
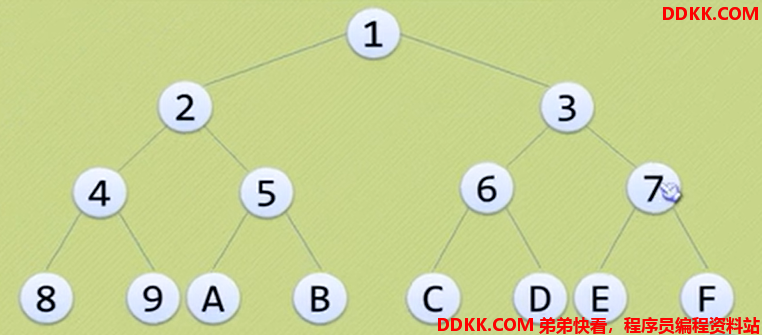
特点:叶子只出现在最后一层;非叶子结点的度为2;在同样深度的二叉树中,满二叉树的结点和叶子最多。
完全二叉树
完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<= i <= n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同,则这棵二叉树成为完全二叉树。
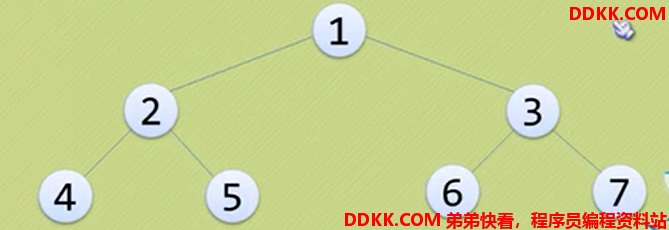
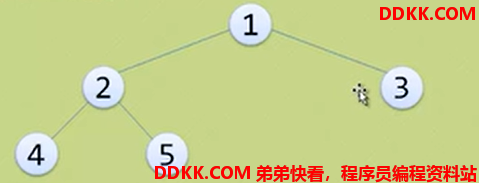
特点:
1、 叶子结点只能出现在最下两层;
2、 最下层的叶子一定集中在左部连续位置;
3、 倒数第二层,若有叶子节点,一定都在右部连续位置;
4、 如果结点度为1,则该结点只有左孩子;
5、 同样结点树的二叉树,完全二叉树的深度最小;
注意:满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。
举例不是完全二叉树的例子
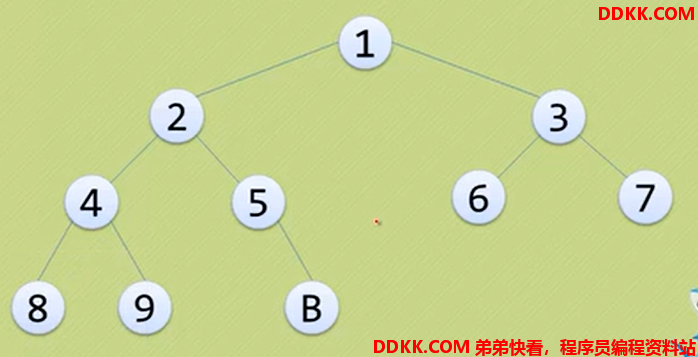
没有A(10),直接到了B(11)
性质
1、 在二叉树的第i层上至多有2^(i-1)个结点(i>=1);
2、 深度为k的二叉树至多有2^k-1个结点;
3、 对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1;
对性质三:
假设度为1的结点数为n1,则二叉树T的结点总数 n = n0 + n1 + n2
其次我们发现连接数总是等于总结点数n - 1,并且等于 n1 + 2 * n2
所以 n0 + n1 + n2 = n1 + 2 × n2,整理即可
4、 具有n个结点的完全二叉树的深度为log2n(取下限)+1;
5、 如果对一棵有n个结点的完全二叉树的结点按层序编号,对任一结点i有以下性质;
->如果i = 1,则结点i是二叉树的根,无双亲;如果i>1,则双亲是结点i/2(取下限)
->如果2i > n,则结点i不做左孩子(是个叶子结点),否则其左孩子是结点2i
->如果2i + 1 > n,则结点i无右孩子(是个叶子结点),否则其右孩子是结点2i + 1
存储结构
顺序存储结构:用一维数组存储二叉树中的各个结点,并且结点的存储位置能体现结点之间的逻辑关系。
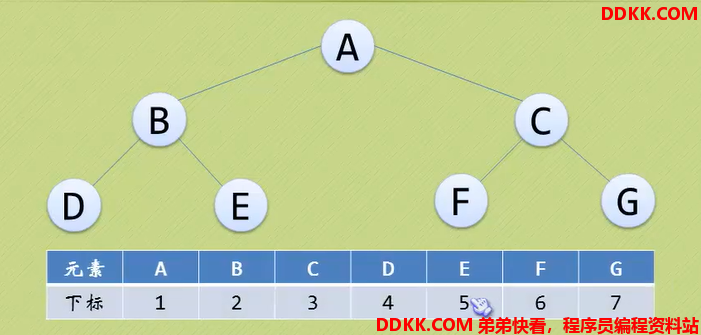
缺点:如果是斜树这种,比较浪费存储空间
链式存储结构:每个结点最多有两个孩子,设计一个数据域和两个指针域。这样的链表叫做二叉链表。


二叉树的遍历
从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点有且只有一次被访问。
遍历方法主要分为四种:前序遍历,中序遍历,后序遍历,层序遍历。
前序遍历
若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。
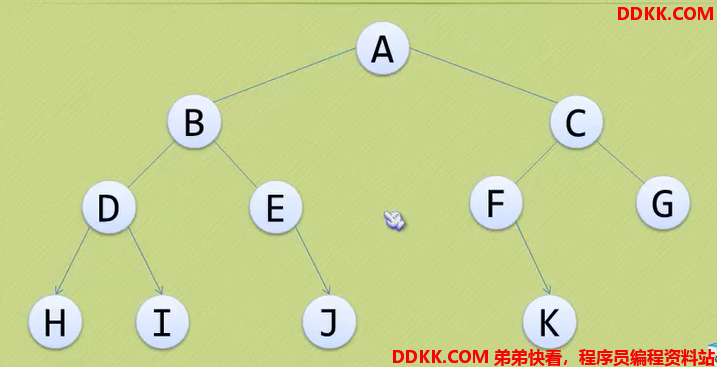
访问顺序:A-B-D-H-I-E-J-C-F-K-G
中序遍历
若二叉树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后访问根结点,再中序遍历右子树。
像上面那个图,顺序为:H-D-I-B-E-J-A-F-K-C-G
后序遍历
若二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点
像上面那个图,顺序为:H-I-D-J-E-B-K-F-G-C-A
层序遍历
若二叉树为空,则空操作返回,否则从树的第一层也就是根结点开始访问,从上而下逐层遍历,在同一层中按照从左到右的顺序对结点逐个访问。
像上面那个图,顺序为:A-B-C-D-E-F-G-H-I-J-K
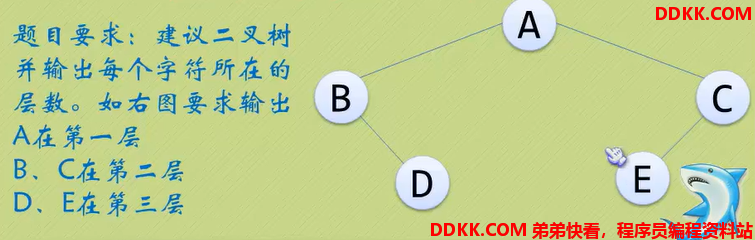
举例并代码实现
#include <stdio.h>
#include <stdlib.h>
typedef char Elemtype
typedef struct BiTNode
{
char data;
struct BiTNode *lchild,* rchild;
}BiTNode,*BiTree;
//创建一个二叉树,假设用户用前序遍历的方式
CreateBiTree(BiTree *T)
{
char c;
scanf("%c",c);
if(' ' == c)
{
*T = NULL;
}
else
{
*T = (BiTNode *)malloc(sizeof(BiTNode));
(*T)->data = c;
CreateBiTree(& (*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
visit(BiTree T,int level)
{
printf("%c 位于第 %d 层",c, level);
}
//前序遍历二叉树
PreOrder Traverse(BiTree T, int level)
{
if(T)
{
visit(T->data,level);
PreOrder Traverse(T->lchild,level + 1);
PreOrder Traverse(T->rchild,level + 1);
}
}
int main()
{
int level = 1;
BiTree T = NULL;
CreateBiTree(&T);
PreOrder Traverse(T, level);
return 0;
}