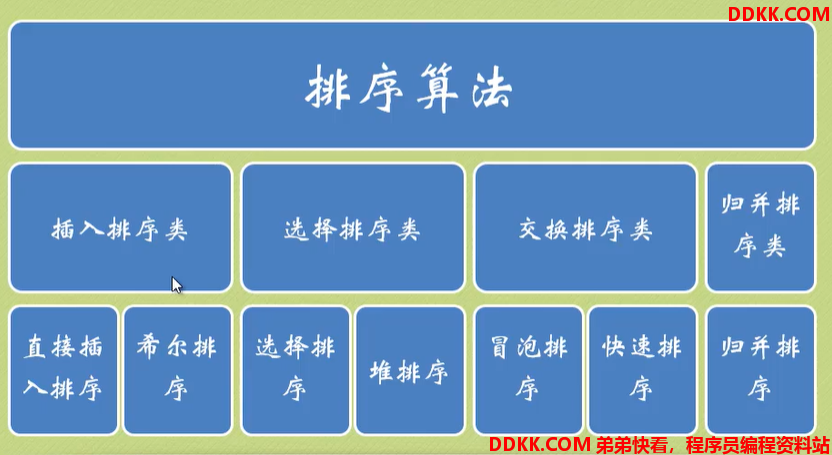
定义

排序的稳定性
假设ki = kj,且在排序前的序列中ri领先于rj(i < j)
如果排序后仍然ri领先,那么称所用的排序方法是稳定的;反之,称为不稳定。
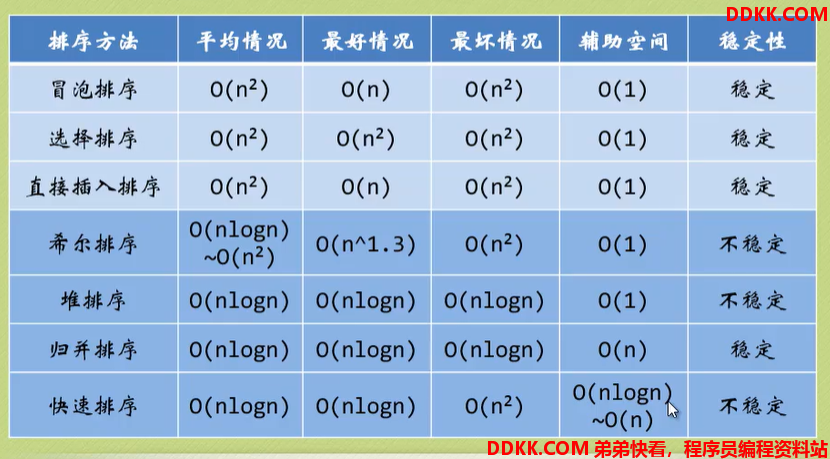
影响因素
时间性能,辅助空间,算法的复杂性。都影响排序的算法性能。
排序算法
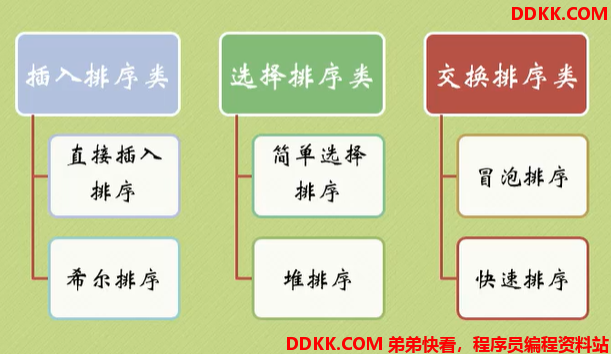
冒泡排序
基本思想:两两相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
要点:
- 两两相邻的元素
- 如果有n个元素,比较n-1次,每一轮减少一次比较
- 从下往上比较,像冒泡泡一样。
原始冒泡排序的算法,这并不符合两两相邻的比较
#include <stdio.h>
void BubbleSort(int k[], int n)
{
int temp;
for(int i = 0;i< n-1; i++)
{
for(int j = i+1; j< n-1 ;j++)
{
if(k[i]> k[j])
{
temp = k[j];
k[j] = k[i];
k[i] = temp;
}
}
}
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
BubbleSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
正宗的冒泡排序算法
#include <stdio.h>
void BubbleSort(int k[], int n)
{
int temp, count1 = 0, count2 = 0;
for(int i=0;i< n-1; i++)
{
for(int j = n-1; j > i ;j--)
{
count1++;
if(k[i]> k[j])
{
count2++;
temp = k[j - 1];
k[j- 1 ] = k[j];
k[j] = temp;
}
}
}
printf("总共进行了%d次比较,进行了%d移动\n",count1,count2);
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
BubbleSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
选择排序
基本思想:通过n-i次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i个记录交换。
(类似原始的冒泡排序,但是区别在于,这个判断完了再交换,而不是立刻更改数据)
#include <stdio.h>
void SelectSort(int k[], int n)
{
int temp, min;
for(int i = 0;i< n-1; i++)
{
for(int j = i+1; j< n-1 ;j++)
{
min = i;
if(k[min]> k[j])
{
min = j;
}
}
if(min != i)
{
temp = k[min];
k[min] = k[i];
k[i] = temp;
}
}
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
SelectSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
效率相对来说比冒泡高一点
直接插入排序算法
基本操作将一个记录插入到已经排好序的有序表中,从而得到一个新的,记录数增加1的有序表。
#include <stdio.h>
void InsertSort(int k[], int n)
{
int temp, min;
for(int i = 1;i< n; i++)
{
if(k[i] < k[i-1])
{
temp = k[i];
for(int j = i-1; k[j] > temp ;j--)
{
k[j + 1] = k[j];
}
k[j + 1] = temp;
}
}
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
InsertSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
希尔排序
第一次跨度为4,第二次跨度为2,第三次跨度为0.
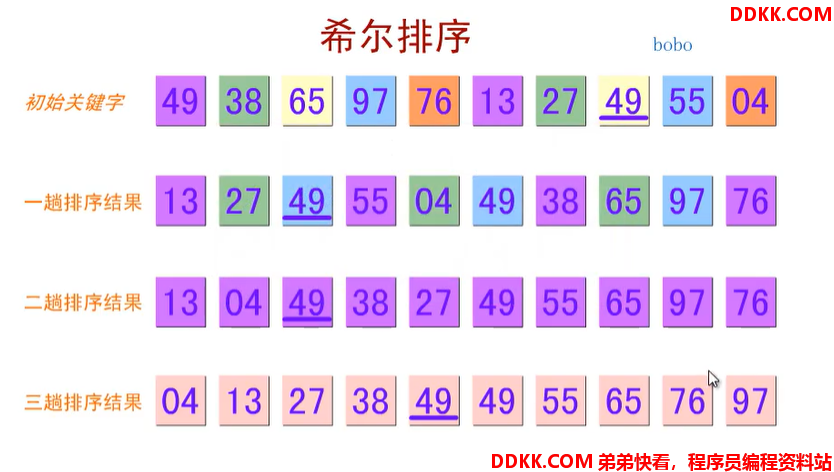
实现代码
#include <stdio.h>
void XierSort(int k[], int n)
{
int temp, min;
int gap = n;
do
{
gap = gap/3 + 1
for(int i = gap;i< n; i++)
{
if(k[i] < k[i-gap])
{
temp = k[i];
for(int j = i-gap; k[j] > temp ;j-=gap)
{
k[j + gap] = k[j];
}
k[j + gap] = temp;
}
}
}while(gap > 1);
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
XierSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
堆排序
之前讲过的排序算法,比较次数比较多,导致算法复杂度增加。
堆排序:对选择排序进行改进,复杂度O(Nlogn),利于之前排序的结果。
大顶堆:每个节点都大于等于其左右孩子的节点。
小顶堆:每个节点都小于等于其左右孩子的节点。
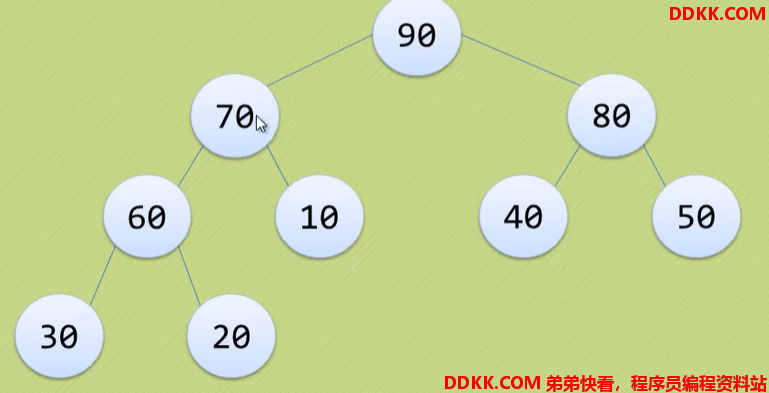
要点:根结点一定是堆中结点最大或者最小的,如果按照层序遍历的方式进行编号,则结点之间满足如下关系
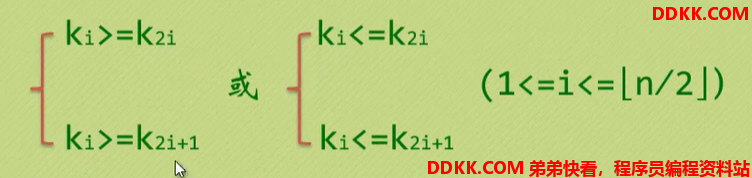
(左为大顶堆,右为小顶堆)下标i与2i和2i+1是双亲和子女关系
则存储结果如下
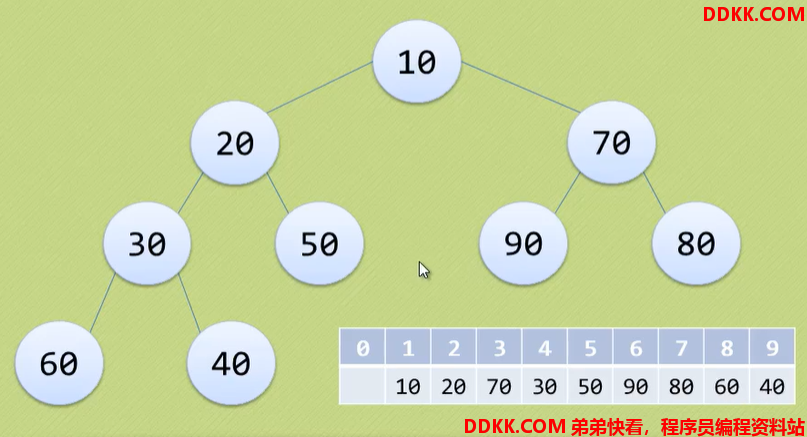
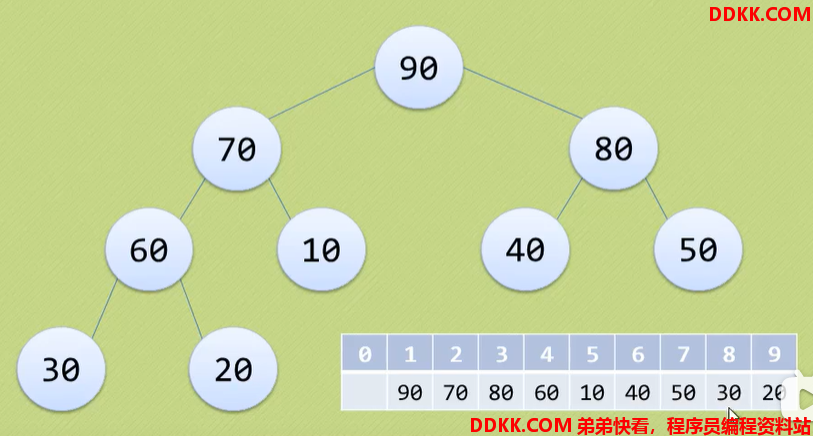
堆排序算法的基本思想:利用堆进行排序的算法
- 将待排序的序列构造成一个大顶堆(小顶堆)
- 此时,整个序列的最大值就是堆顶的根结点,将它移走(就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值)
- 然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的此大值。
- 如此反复执行,得到一个有序序列
#include <stdio.h>
void HeapAdjust(int k[],int s, int n)
{
int i, temp;
temp = k[s];
for(i = 2*s;i <=n;i *=2)
{
if(i< n && k[i] < k[i+1])
{
i++;
}
if(temp >=k[i])
{
break;
}
k[s] = k[i];
s = i;
}
k[s] = temp;
}
void swap(int k[],int i, int j)
{
int temp;
temp = k[i];
l[i] = k[j];
k[j] = temp;
}
void HeapSort(int k[], int n)
{
int i ;
for(i = n/2; i> 0;i--)
{
HeapAdjust(k ,i , n);
}
for(i =n;i >1; i++)
{
swap(k, 1, i);
HeapAdjust(k ,1 , i-1);
}
}
int main()
{
int i ,a[10] = {
-1,5,2,6,0,3,9,1,7,4};
HeapSort(a,9);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
归并排序
归并排序:就是利用归并的思想实现的排序方法,原理是假设初始序列有n个记录,可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到n/2(向上取整)个长度为2或1 的有序子序列,再两两归并,如此重复,直到得到一个长度为n的有序序列为止,这种排序方法称为2路归并排序。
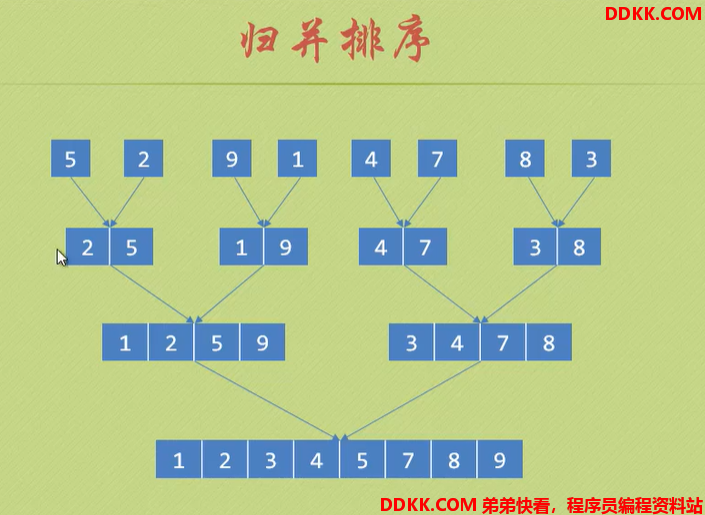
递归实现
#include <stdio.h>
//实现归并,把结果存在list1里面
void merging(int *list1,int list1_size, int *list2, int list2_size)
{
int temp[MAXSIZE];
int i, j ,k, m;
while(i < list1_size && j< list2_size)
{
if(list1[i]<list2[j])
{
temp[k++] = list1[i++];
}
else
{
temp[k++] = list2[j++];
}
}
while(i < list1_size)
{
temp[k++] = list1[i++];
}
while(j < list2_size)
{
temp[k++] = list1[j++];
}
for( m=0; m< (list1_size + list2_size);m++)
{
list1[m] = temp[m];
}
}
void MergeSort(int k[], int n)
{
if(n >1)
{
int *list1 = k;
int list1_size = n/2;
int *list2 = k + n/2;
int list1_size = n - list1_size;
MergeSort(list1 , list1_size);
MergeSort(list2 , list2_size);
merging(list1,list1_size,list2,list2_size);
}
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
MergeSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
迭代实现
#include <stdio.h>
#define MAXSIZE 10
void MergeSort(int k[], int n)
{
int i ,left_min,left_max,right_min,right_max;
int *temp = (int *)malloc (n * sizeof(int));
for(i = 1;i<n; i *=2)
{
for( left_min = 0;left_min < n-i; letf_min = right_max)
{
right_min = left_max = left_min + i;
right_max = left_max + i;
if(right_max >n)
{
right_max = n;
}
next = 0
while(left_min <left_max && right_min <right_max)
{
if(k[left_min] < k[right_min]
{
temp[next++] = k[left_min];
}
else
{
temp[next++] = k[right_min];
}
}
while(left_min <left_max)
{
k[--right_min] = k[--left_min];
}
while(next >0)
{
k[--right_min] =temp[--next];
}
}
}
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
MergeSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
快速排序算法
#include <stdio.h>
void swap(int k[],int low , int high)
{
int temp;
temp = k[low];
k[low] = k[high];
k[high] = temp;
}
int Partition(int k[],int low, int high)
{
int point;
point = k[low];
while(low <high)
{
while(low <high && k[high] >= point)
{
high--;
}
swap(k ,low,high);
while(low <high && k[low] <= point)
{
low++;
}
swap(k ,low,high);
}
return low;
}
void QSort(int k[], int low, int high)
{
int point;
if(low< high)
{
point = Partition(k,low,high); //计算基准点计算,一般选取第一个作为基准点
QSort(k,low,point-1);
QSort(k,point +1,high);
}
}
void QuickSort(int k[], int n)
{
QSort(k,0,n-1);
}
int main()
{
int i ,a[10] = {
5,2,6,0,3,9,1,7,4,8};
QuickSort(a,10);
printf("排序后: \n");
for(i = 0;i < 10; i++)
printf("%d\t",a[i]);
printf("\n");
}
总结