广度优先遍历
广度优先遍历BreadthFirstSearch,也称广度优先搜索,简称BFS。
可以利用队列实现堆图的广度优先遍历。
下面代码是邻接矩阵代码实现,只有部分代码
#include <stdio.h>
void BFETraverse(MGraph G)
{
int i,j;
Queue Q;
for(i = 0; i < G.numVertexse; i++)
{
visited[i] = FALSE;
}
initQueue( &Q);
for(i =0; i< G.numVertexse; i++)
{
if(!visited[i]
{
printf("%c ",G.vex[i]);
visited[i] = TRUE;
EnQueue(& Q, i);
while(! QueueEmpty(Q))
{
DeQueue( &Q, &i);
for( j =0; j < G.numVertexse ; j++)
{
if(G.art[i][j] == 1 && !visited[j])
{
printf("%c ",G.vex[j]);
visited[j] = TRUE;
EnQueue(& Q, j);
}
}
}
}
}
}
带权最小生成树-- 普里姆算法
如下图,生成了一棵树,但是成本比较高。
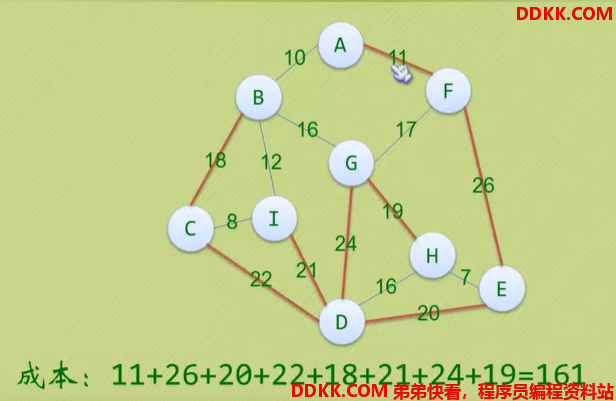
采用上述方法,成本比较高,现在来看方案二和方案三的生成树
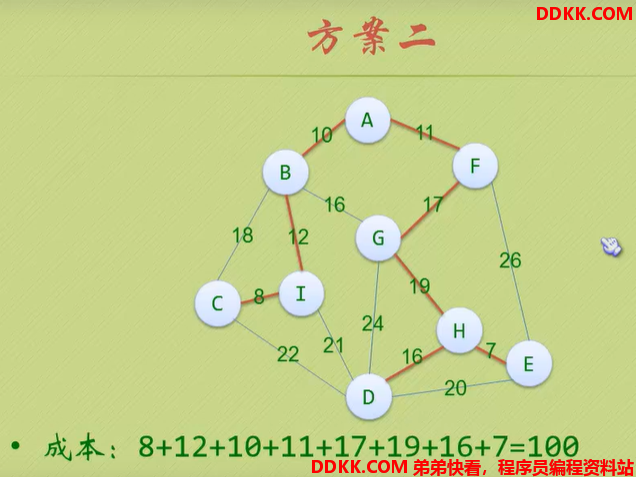
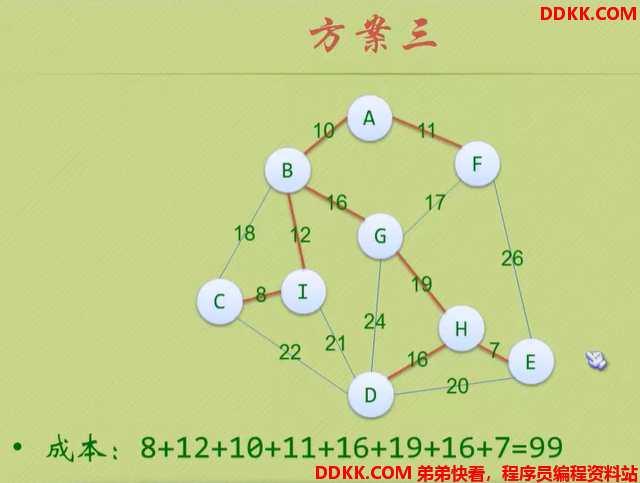
下面讲普里姆算法的思路与分析
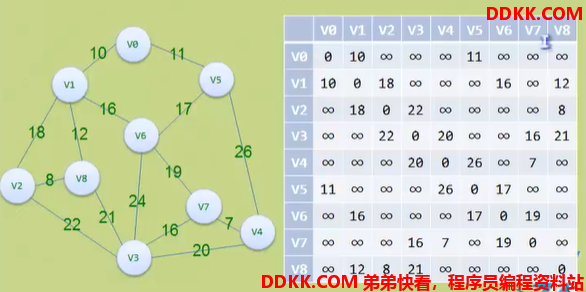
生成了邻接矩阵,数值代表权值,∞代表不连接,0代表自己。
普里姆算法:以某顶点为起点,逐步找各个顶点上最小权值的边来构建最小生成树的。
下面是代码实现
void MiniSpanTree_Prim(MGraph G)
{
int min,i,j,k;
int adjvex[MAXVEX]; //存放相关顶点的下标,0代表没有相连,1代表有联系
int lowcost[MAXVEX]; //存放相关顶点间边的权值
lowcost[0] = 0; //V0作为最小生成树的根开始遍历,权值为0
adjvex[0] = 0; //V0第一个加入
//初始化操作
for( i = 1; i<G.numVertexes;i++)
{
lowcost[i] = G.arc[0][i]; //将邻接矩阵第0行所有权值先加入数组
adjvex[i] = 0; //初始化全部纤维V0的下标
}
//真正构造最小生成树的过程
for( i = 1; i< G;i++)
{
min = INFINITY; //初始化最小权值为65535等不可能数值
j= 1;
k = 0;
//遍历全部顶点
while(j < G.numVertexes)
{
//找出来lowcost数组已存储的最小权值
if(lowcost[j] !=0 && lowcost[j] < min)
{
min = lowcost[j];
k = j; //将发现的最小权值的下标存入k,以待使用
}
j++;
}
//打印当前顶点边中权值最小的边
printf("(%d,%d)",adjvex[k],k);
lowcost[k] = 0; //将当前的顶点权值设置为0,表示此顶点已经完成任务,进行下一个顶点的遍历
//邻接矩阵k行逐个遍历全部顶点
for(j = ; j< G.numVertexes ;j++)
{
if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j] )
{
lowcost[j] = G.arc[k][j];
adjvex[j] = k;
}
}
}
}
带权最小生成树-- 克鲁斯卡尔算法
考虑出发点:为了使生成树上的权值之和达到最小,则应使生成树中每一条边的权值尽可能地小。
克鲁斯卡尔算法:从边出发,直接去找最小权值的边构建生成树。
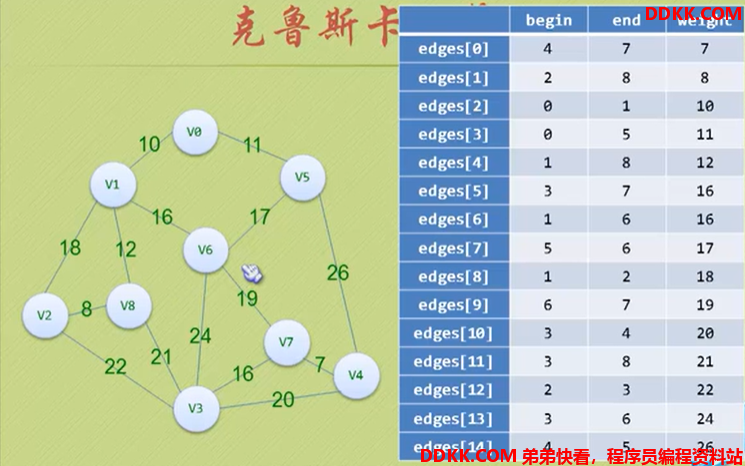
代码实现
int Find(int *parent, int f)
{
while(parent(f) > 0)
{
f = parent(f);
}
return f;
}
//Kruskal 算法生成最小生成树
void MiniSpanTree_Kruskal(MGraph G)
{
int i, n ,m;
Edge edges[MAGEDGE]; //定义边集数组
int parent[MAXVEX]; //定义parent数组用来判断边与边是否形成回路
for(i = 0; i< G.numVertexes; i++)
{
parent[i] = 0;
}
for(i = 0;i <G.numEdges ; i++)
{
n = Find(parent , edges[i].begin); // 4 2 0 1 5 3 8 6 6 6 7
n = Find(parent, edges[i].end); // 7 8 1 5 8 7 6 6 6 7 7
if( n!= m) //如果n==m,则形成环路,不满足
{
parent[n] = m;//将此边的结尾顶点放入下标为起点的parent数组中,表示此顶点已经在生成树集合中
printf("(%d, %d) %d",edges[i].begin ,edges[i].end,edges[i].weight);
}
}
}
最短路径之迪杰斯特拉算法
最短路径:
- 在网图中,两顶点经过的边上权值之和最少的路径。
- 非网图是两顶点之间经过的边数最少的路径。
路径开始的第一个顶点称为源点,最后一个顶点称为终点。
迪杰斯特拉算法:基于已经求出的最短路径的基础上,求得更远顶点的最短路径,最后得到结果。
实现代码如下
#define MAXVEX 9
#define INFINITY 65535
typedef int Patharc[MAXVEX]
typedef int ShortPathTable[MAXVEX]
void ShortestPath_Dijkstar(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
int v,w,k,min;
int final[MAXVEX]; //已经求得顶点V0到Vw的最短路径
//初始化数据
for(v = 0; v< G.numVertexes ; v++)
{
final[v] = 0; //全部顶点初始化为未找到路径
(*D)[v]= G.arc[V0][v]; //将与 V0有连接线的顶点加上权值
(*P)[v] = 0; //初始化路径数组P为0
}
(*D)[V0] = 0; //V0到V0的路径为0
final[V0] = 1; //V0到V0不需要求路径
//开始主循环,每次求得V0到某个V顶点的最短路径
for( v=1;v< G.numVertexes ;v++)
{
min = INFINITY;
for( w = 0; w< G.numVertexes ;w++)
{
k = w;
min = (*D)[w];
}
final[k] = 1; //将目前找到的最近顶点置为1
//修正当前最短路径及距离
for(w = 0;w < G.numVertexes ;w++)
{
//如果经过v顶点的路径比现在这条短的话,更新
if(!final[w] && (min + G.arc[k][w] < (*D)[w]))
{
(*D)[w] = min + G.arc[k][w];
(*p)[w] = k;
}
}
}
}
最短路径之弗洛伊德算法
弗洛依德算法求所有顶点到所有顶点的最短路径,并且算法简洁。
代码实现
#define MAXVEX 9
#define INFINITY 65535
typedef int Pathmatirx[MAXVEX][MAXVEX]
typedef int ShortPathTable[MAXVEX][MAXVEX]
void ShortestPath_Floyd(MGraph G, int V0, Pathmatirx*P, ShortPathTable *D)
{
int v,w,k;
//初始化数据
for(v = 0; v< G.numVertexes ; v++)
{
(*D)[v][w]= G.arc[v][w];
(*P)[v][w] = w;
}
for( k=0;v< G.numVertexes ;k++)
{
for( v = 0; v< G.numVertexes ;v++)
{
for(w = 0;w < G.numVertexes ;w++)
{
if((*D)[v][w] > (*D)[v][k] + (*D)[k][w])
{
(*D)[v][w] = (*D)[v][k] + (*D)[k][w]
(*P)[v][w] = (*P)[v][k];
}
}
}
}
}