约瑟夫环
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第3个人。接着,杀掉第3个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
约瑟夫问题和循环链表相同。
问题:用循环链表模拟约瑟夫问题,把41个人自杀的顺序编号输出。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int data;
struct node *next;
}node;
node *create(int n)
{
node *p = NULL, *head;
head = (node*)malloc(sizeof(node));
p = head;
node *s;
int i = 1;
if( n != 0)
{
while(i<=n)
{
s = (node*)malloc(sizeof(node));
s->data = i;
i++;
p->next = s;
p = s;
}
s->next = head->next;//不指向头节点,而是第一个结点,构成一个环,释放头结点
}
free(head)
return s->next;
}
int main()
{
int n = 41;
int m = 3;
int i;
node *p = create(n);
node *temp;
m %= n; //在这里是2
while( p != p->next )
{
for(i = 1; i < m-1; i++)
{
p = p->next;
}
printf("%d -> ",p->next->data);
temp = p->next;
p->next = temp->next;
free(temp);
p = p->next;
}
printf("%d\n",p->data);
return 0;
}
循环链表的改进
去掉头指针,将尾指针指向头结点

判断空链表的条件:rear是否等于rear->next。
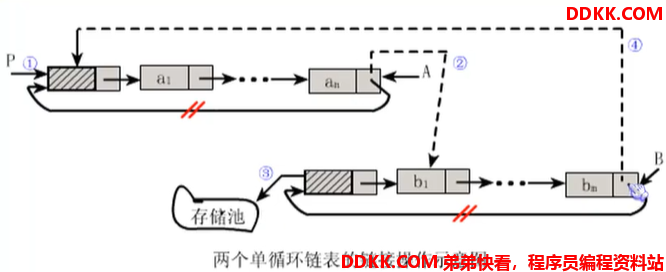
例题1:实现将两个链表连接成一个线性表(a1, a2, a3…b1, b2…)的运算
普通思路:用头指针表示的单循环表上,遍历第一个链表,找到an,然后将b1放在an的后面,bn的next指向a的头结点。执行时间为O(n)
优化思路:只需要修改二者的尾指针
例题2:判断单链表中是否有环(链表的尾结点指向了链表中的某个结点)
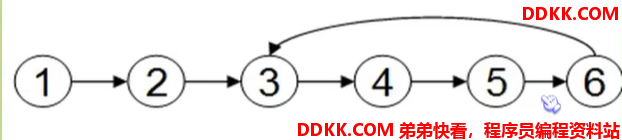
方法一:使用p,q两个节点,p总是向前走,q是每次从头开始走,对于每个结点,看p的步数和q是否一样。例如,p从1-2-3-4-5-6-3,用了6步,此时q从head出发,只需要两步,因此步数不等,存在环。
方法二:快慢指针,p向前走一步,q走两步,某个时候p==q,则存在环。
魔术师发牌问题
一位魔术师掏出一叠扑克牌,魔术师取出其中13张黑桃,洗好后,把牌面朝下。说:“我不看牌,只数一数就能知道每张牌是什么?”魔术师口中念一,将第一张牌翻过来看正好是A;魔术师将黑桃A放到桌上,继续数手里的余牌,第二次数1,2,将第一张牌放到这叠牌的下面,将第二张牌翻开,正好是黑桃2,也把它放在桌子上。第三次数1,2,3,前面二张牌放到这叠牌的下面,取出第三张牌,正好是黑桃3,这样依次将13张牌翻出,全部都准确无误。求解:魔术师手中牌的原始顺序是什么样子的?
代码如下:
#include <stdio.h>
#include <stdlib.h>
#define CardNumber 13
typedef struct node
{
int data;
struct node *next;
}sqlist,*linklist;
linklist CreateLinkList()
{
linklist head = NULL;
linklist s, r;
int i;
r = head;
for(i = 1; i<= CardNumber ; i++)
{
s = (linklist)malloc(sizeof(sqlist));
s->data = 0;
if(head == NULL)
head = s;
else
r->next = s;
r=s;
}
r->next = head;
return head;
}
//发牌顺序计算
void Magician(linklist head)
{
linklist p;
int j;
int Countnumber = 2;
p = head;
p->data = 1; //第一张牌放1
while(1)
{
for( j = 0 ;j <Countnumber ; j++)
{
p = p->next;
if(p->data != 0)
{
p->next;
j--;
}
}
if(p->data == 0)
{
p->data = Countnumber;
Countnumber++;
if(Countnumber == 14)
break;
}
}
}
int main()
{
linklist p ;
int i;
p = CreateLinkList();
Magician(p);
printf("排列顺序:\n");
for(i = 0; i < CardNumber ; i++)
{
printf("黑桃%d", p->data);
p = p->next;
}
return 0;
}
双向链表
结点结构

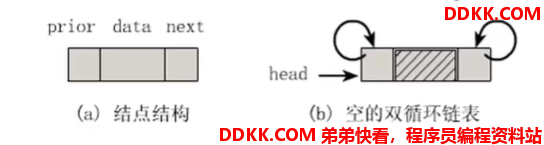
插入操作
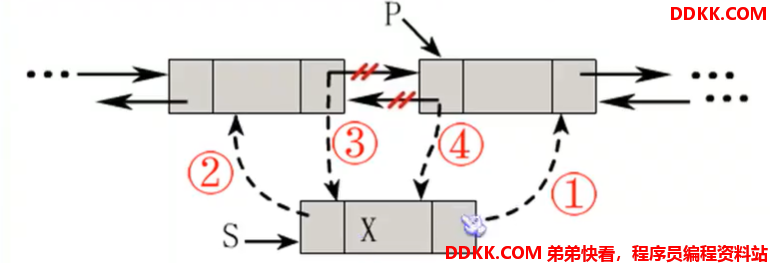

删除操作
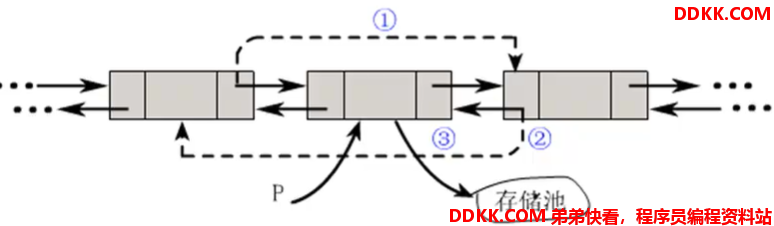

例题
要求实现用户输入一个数使得26个字母的排列发生变化,例如用户输入3,输出结果:DEFGHIJKLMNOPQRSTUVWXYZABC。也支持负数输入,例如-3,XYZABCDEFGHIJKLMNOPQRSTUVW
代码实现如下:
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
typedef char ElemType;
typedef int Status;
typedef struct DualNode
{
ElemType data;
struct DualNode *prior;
struct DualNode *next;
}DualNode, *DuLinkList;
Status InitList(DuLinkList *L)
{
DualNode *p,*q;
int i;
*L = (DuLinkList)malloc(sizeof(DualNode));
if(!(*L))
return ERROR;
(*L)->next = (*L)->prior = NULL;
p = (*L);
for(i = 0; i < 26; i ++)
{
q = (DuLinkList)malloc(sizeof(DualNode));
if(!q)
return ERROR;
q->data = 'A' + i;
q->prior = p;
q->next = p->next;
p->next = q;
p = q;
}
p->next = (*L)->next;
(*L)->next->prior = p;
return OK;
}
void Caesar(DuLinkList *L, int i)
{
if( i > 0)
{
do
{
(*L) = (*L)->next;
}while( --i);
}
if( i < 0)
{
do
{
(*L) = (*L)->next;
}while( ++i);
}
}
int main()
{
DuLinkList L;
int i,n ;
InitList(&L);
printf("请输入一个整数:");
scanf("%d",&n);
printf("\n");
Caesar(&L ,n );
for(i = 0; i< 26 ;i ++)
{
L = L->next;
printf("%c", L->data);
}
return 0;
}