题目地址: https://leetcode.com/problems/minimum-genetic-mutation/description/
题目描述
Agene string can be represented by an 8-character long string, with choices from "A", "C", "G", "T".
Suppose we need to investigate about a mutation (mutation from "start" to "end"), where ONE mutation is defined as ONE single character changed in the gene string.
Forexample, "AACCGGTT" -> "AACCGGTA" is 1 mutation.
Also, there is a given gene "bank", which records all the valid gene mutations. A gene must be in the bank to make it a valid gene string.
Now, given 3 things - start, end, bank, your task is to determine what is the minimum number of mutations needed to mutate from "start" to "end". If there is no such a mutation, return -1.
Note:
1、 Startingpointisassumedtobevalid,soitmightnotbeincludedinthebank.;
2、 Ifmultiplemutationsareneeded,allmutationsduringinthesequencemustbevalid.;
3、 Youmayassumestartandendstringisnotthesame.;
Example 1:
start: "AACCGGTT"
end: "AACCGGTA"
bank: ["AACCGGTA"]
return: 1
Example 2:
start: "AACCGGTT"
end: "AAACGGTA"
bank: ["AACCGGTA", "AACCGCTA", "AAACGGTA"]
return: 2
Example 3:
start: "AAAAACCC"
end: "AACCCCCC"
bank: ["AAAACCCC", "AAACCCCC", "AACCCCCC"]
return: 3
题目大意
给出了一个起始基因 start,一个结束基因 end。
问能不能通过变换,每次变化当前基因的一位,并且变化后的这个基因在基因库中的为有效基因,最后变换成为 end。如果可以的话,返回变换的最小次数。如果不可以的话,返回 -1.
以题目的示例 2 为例:
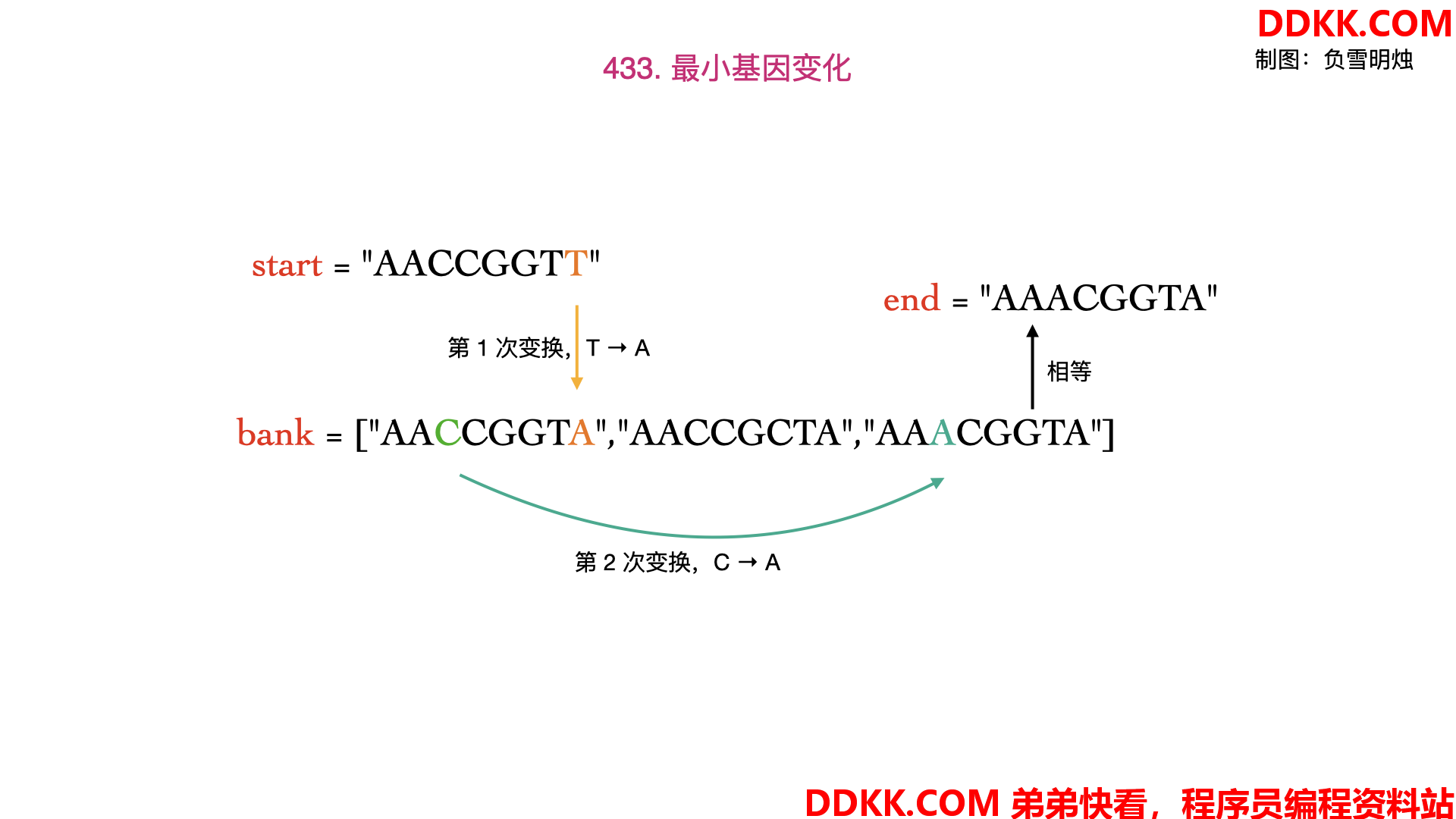
输入:start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出:2
变化的过程如下所示:
解题方法
BFS
基本和 127. Word Ladderopen in new window 一模一样的,只不过把 26 个搜索换成了 4 个搜索,所以代码只用改变搜索的范围,以及最后的返回值就行了。
很显然这个问题是 BFS 的问题,同样是走迷宫问题的 4 个方向。
分享 BFS 模板:
BFS使用队列,把每个还没有搜索到的点依次放入队列,然后再弹出队列的头部元素当做当前遍历点。
BFS总共有两个模板:
模板一:
如果不需要确定当前遍历到了哪一层,BFS 模板如下。
while queue 不空:
cur = queue.pop()
if cur 有效且未被访问过:
进行处理
for 节点 in cur 的所有相邻节点:
if 该节点有效:
queue.push(该节点)
1 2 3 4 5 6 7
模板二:
如果要确定当前遍历到了哪一层,BFS 模板如下。 这里增加了 level 表示当前遍历到二叉树中的哪一层了,也可以理解为在一个图中,现在已经走了多少步了。size 表示在当前遍历层有多少个元素,也就是队列中的元素数,我们把这些元素一次性遍历完,即把当前层的所有元素都向外走了一步。
level = 0
while queue 不空:
size = queue.size()
while (size --) {
cur = queue.pop()
if cur 有效且未被访问过:
进行处理
for 节点 in cur的所有相邻节点:
if 该节点有效:
queue.push(该节点)
}
level ++;
1 2 3 4 5 6 7 8 9 10 11 12
上面两个是通用模板,在任何题目中都可以用,是要记住的!
本题做法
由于本题需要知道变换了多少次,因此需要确定当前遍历到哪一层,故本题中直接套用模板二。
代码总体思路:
-
利用队列保存有效的字符串
-
只要队列不空,就持续循环:
-
记录当前队列的长度,对队列中该长度的字符串逐一遍历:
-
如果搜索到
end,直接返回当前的步数step -
否则,对当前字符串中的每个字符,都转变成
ACGT四个字符,看新形成的字符串是否遇到过- 如果没遇到过,就放入队列之中。
-
-
步数 + 1
其中判断字符串是否遇到过,有两种方法:
- 使用 set 保存所有已经遇到过的字符串;
- 直接从 bank 中删除已经遇到过的字符串。
Python, C++ 代码如下:
class Solution(object):
def minMutation(self, start, end, bank):
"""
:type start: str
:type end: str
:type bank: List[str]
:rtype: int
"""
bfs = collections.deque()
bfs.append((start, 0))
bankset = set(bank)
while bfs:
gene, step = bfs.popleft()
if gene == end:
return step
for i in range(len(gene)):
for x in "ACGT":
newGene = gene[:i] + x + gene[i+1:]
if newGene in bank and newGene != gene:
bfs.append((newGene, step + 1))
bank.remove(newGene)
return -1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
class Solution {
public:
int minMutation(string start, string end, vector<string>& bank) {
unordered_set<string> bank_set(bank.begin(), bank.end());
queue<string> que;
que.push(start);
unordered_set<string> visited;
visited.insert(start);
int step = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
string cur = que.front(); que.pop();
if (cur == end) {
return step;
}
for (char gene : "ACGT") {
for (int j = 0; j < cur.size(); ++j) {
string next = cur;
next[j] = gene;
if (bank_set.count(next) && !visited.count(next)) {
que.push(next);
visited.insert(next);
}
}
}
}
step ++;
}
return -1;
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
class Solution {
public:
int minMutation(string start, string end, vector<string>& bank) {
queue<string> q;
const int N = start.size();
q.push(start);
int step = 0;
while (!q.empty()) {
int size = q.size();
for (int s = 0; s < size; s++) {
auto cur = q.front(); q.pop();
if (cur == end) {
return step;
}
for (int i = 0; i < N; i++) {
for (char n : {'A', 'C', 'G', 'T'}) {
string next = cur.substr(0, i) + n + cur.substr(i + 1);
if (next == cur) continue;
for (auto it = bank.begin(); it < bank.end(); ++it) {
if (*it == next) {
q.push(next);
bank.erase(it);
break;
}
}
}
}
}
step += 1;
}
return -1;
}
};
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
复杂度
- 时间复杂度:O(N∗L),其中 N是 Bank 中的单词个数,L是基因的长度。
- 空间复杂度:O(N)
总结
1、 BFS模板题,而且出现频率挺高的,记住我的模板就行;
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发