1. 首页
  2. 系列专栏
  3. LeetCode题解汇总

449. Serialize and Deserialize BST 序列化和反序列化二叉搜索树

分类：LeetCode题解汇总 标签：LeetCode刷题笔记，LeetCode，Java，Python，C++，题库，版本，刷题，攻略，经验，指南，笔记，顺序

关键词：力扣，LeetCode，算法，题解，解析，449，Python, C++, 二叉搜索树，序列化，反序列化

题目地址：https://leetcode.cn/problems/serialize-and-deserialize-bst/open in new window

题目描述

序列化是将数据结构或对象转换为一系列位的过程，以便它可以存储在文件或内存缓冲区中，或通过网络连接链路传输，以便稍后在同一个或另一个计算机环境中重建。

设计一个算法来序列化和反序列化 二叉搜索树 。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串，并且可以将该字符串反序列化为最初的二叉搜索树。

编码的字符串应尽可能紧凑。

示例1：

输入：root = [2,1,3]
输出：[2,1,3]

示例2：

输入：root = []
输出：[]

提示：

  • 树中节点数范围是 [0, 10^4]
  • 0 <= Node.val<= 10^4
  • 题目数据 保证 输入的树是一棵二叉搜索树。

来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/serialize-and-deserialize-bst 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目大意

首先要明白题意：

  • 序列化：把内存中的二叉搜索树转成字符串；
  • 反序列化：把字符串恢复成内存中的二叉搜索树。

 

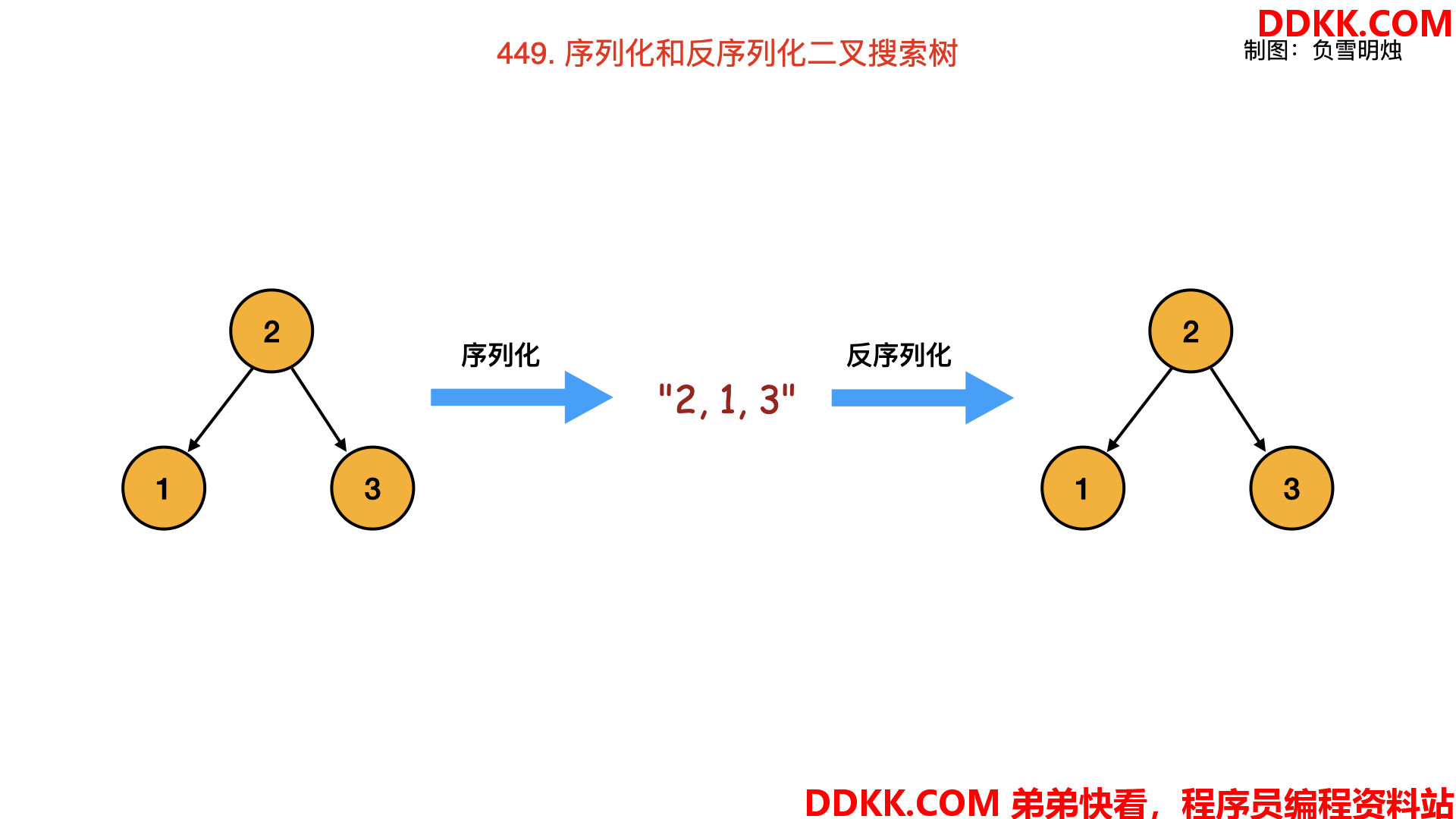
题目没有限定我们用什么方法，只要求我们序列化后的字符串尽可能紧凑。

解法不固定，只要序列化后的结果，能被反序列化函数还原成一模一样的二叉搜索树（BST） ，都认为是正确答案。

评测的过程是下面这样：

Codec ser = new Codec();
Codec deser = new Codec();
String tree = ser.serialize(root);
TreeNode ans = deser.deserialize(tree);
return ans;

1 2 3 4 5

解题方法

前序遍历 + 递归

BST的基本定义：

  • BST 的左子树所有节点都比根节点值小，右子树所有节点都比根节点值大。

只知道树的一种遍历方式，是没法确定这个树的，BST 也不例外。

因此，我的主要思路就是：采用前序遍历的序列化 BST，再根据 BST 的性质进行反序列化。

1、 序列化的过程：

采用前序遍历，转化成字符串。

 

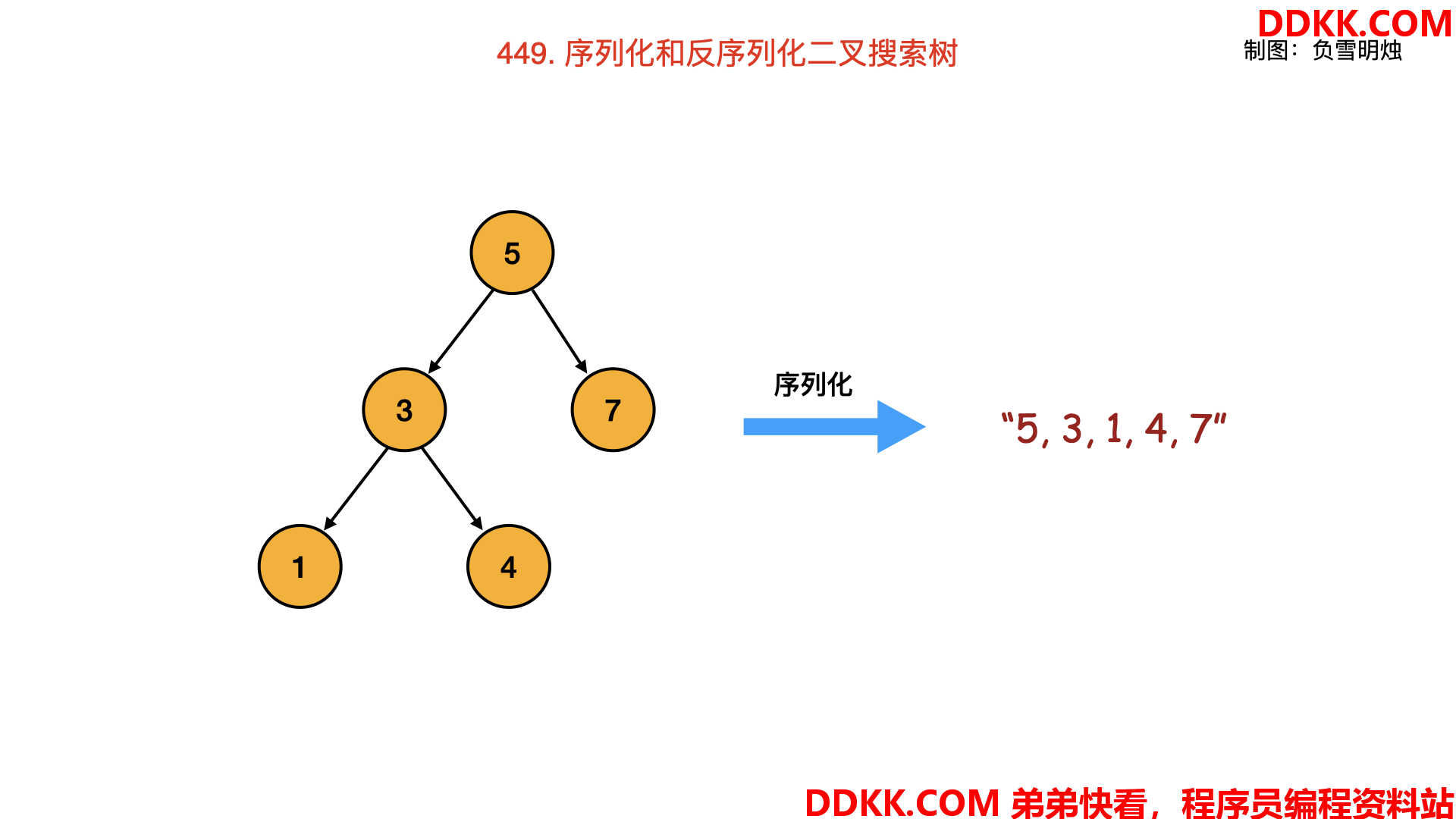
1、 反序列化的过程：

  • 前序遍历得到的数组的第一个值就是 BST 的根节点
  • 数组后面的这些数中比根节点的值小的是根节点的左子树，比根节点值大的是根节点的右子树
  • 递归就可以反序列化出原本的 BST

 

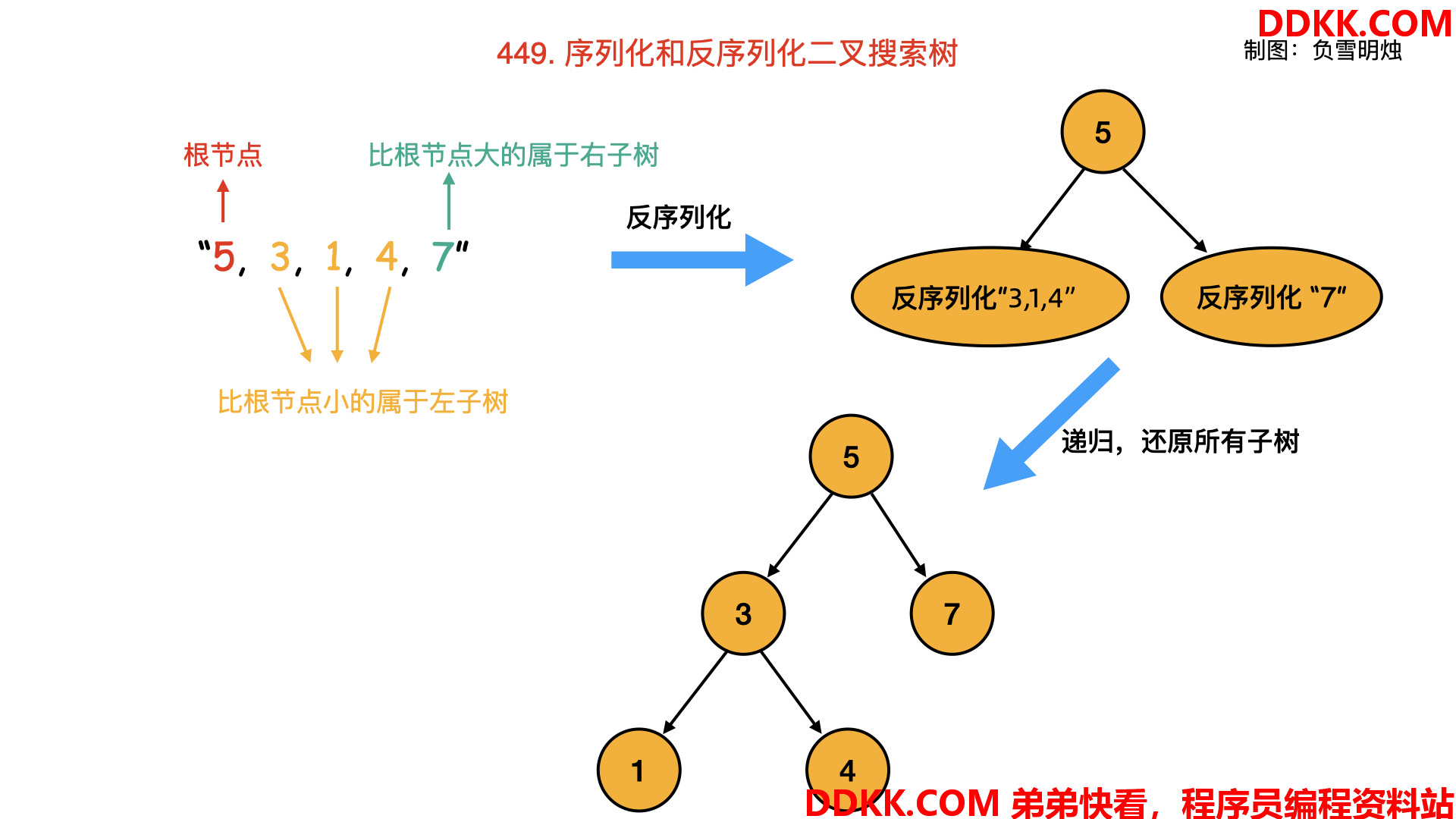
Python语言代码如下：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        vals = []
        def preOrder(root):
            if root:
                vals.append(root.val)
                preOrder(root.left)
                preOrder(root.right)
        preOrder(root)
        return ','.join(map(str, vals))
    def deserialize(self, data):
        if not data or data == '':
            return None
        vals = map(int, data.split(","))
        root = TreeNode(vals[0])
        leftVals = [x for x in vals if x < vals[0]]
        rightVals = [x for x in vals if x > vals[0]]
        root.left = self.deserialize(",".join(map(str, leftVals)))
        root.right = self.deserialize(",".join(map(str, rightVals)))
        return root
        

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# tree = ser.serialize(root)
# ans = deser.deserialize(tree)
# return ans

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

C++代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:

    void preOrder(TreeNode* root, vector<int>& res) {
        if (!root) return;
        res.push_back(root->val);
        preOrder(root->left, res);
        preOrder(root->right, res);
    }

    string vector2string(vector<int>& vals) {
        string res;
        if (vals.empty()) return res;
        for (int i = 0; i < vals.size() - 1; ++i) {
            res += to_string(vals[i]) + ",";
        }
        res += to_string(vals[vals.size() - 1]);
        return res;
    }

    vector<int> split(string& s) {
        vector<int> res;
        size_t pos = 0;
        std::string token;
        while ((pos = s.find(",")) != std::string::npos) {
            token = s.substr(0, pos);
            res.push_back(stoi(token));
            s.erase(0, pos + 1);
        }
        res.push_back(stoi(s));
        return res;
    }

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        vector<int> vals;
        preOrder(root, vals);
        return vector2string(vals);
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        if (data.empty()) return nullptr;
        vector<int> vals = split(data);
        TreeNode* root = new TreeNode(vals[0]);
        vector<int> leftVals;
        vector<int> rightVals;
        for (int val : vals) {
            if (val < vals[0]) {
                leftVals.push_back(val);
            } else if (val > vals[0]) {
                rightVals.push_back(val);
            }
        }
        root->left = deserialize(vector2string(leftVals));
        root->right = deserialize(vector2string(rightVals));
        return root;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec* ser = new Codec();
// Codec* deser = new Codec();
// string tree = ser->serialize(root);
// TreeNode* ans = deser->deserialize(tree);
// return ans;

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75

复杂度：

  • 时间复杂度：序列化是 O(N)；反序列化最差达到 O(N2)，因为当树的节点都偏向于一侧的时候，每遍历一个节点，都要对访问剩余的 N−1个节点。
  • 空间复杂度：序列化是 O(N)；反序列化最差达到 O(N2)，理由同上。

前序遍历 + 队列

在反序列化的过程中，也可以通过一个队列进行操作。

python 代码如下：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:
    
    def serialize(self, root):
        """Encodes a tree to a single string.
        :type root: TreeNode
        :rtype: str
        """
        vals = []
        def preOrder(root):
            if root:
                vals.append(root.val)
                preOrder(root.left)
                preOrder(root.right)
        preOrder(root)
        return ' '.join(map(str, vals))

    
    def deserialize(self, data):
        """Decodes your encoded data to tree.
        :type data: str
        :rtype: TreeNode
        """
        vals = collections.deque(int(val) for val in data.split())
        def build(minVal, maxVal):
            if vals and minVal < vals[0] < maxVal:
                val = vals.popleft()
                root = TreeNode(val)
                root.left = build(minVal, val)
                root.right = build(val, maxVal)
                return root
        return build(float('-inf'), float('inf'))

# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.deserialize(codec.serialize(root))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

总结

1、 没有固定套路的题目，需要自己发掘数据结构的性质，找到合适的解法；

DDKK.COM 弟弟快看-教程，程序员编程资料站，版权归原作者所有

本文经作者：负雪明烛 授权发布，任何组织或个人未经作者授权不得转发