1. 分治算法
步骤
1、 问题拆分成多个小问题,相互独立;
2、 若问题较简单可直接解,否则递归的解各个子问题;
3、 将各个子问题合并为原问题的解;
使用分治思想的算法
排序:合并、归并排序
二分搜索、大整数乘法、棋盘覆盖
线性时间选择、最接近点对问题、循环赛日程表
汉诺塔
1.1 汉诺塔
package top.linruchang.algorithm.commonAlgorithms;
/**
* @Classname HanoiTower
* @Description
* @Date 2022/4/16 22:33
* @Created by lrc
*/
public class HanoiTower {
public static void show(int plateNum, char firstTower, char secondTower, char thirdTower) {
if(plateNum == 1) {
System.out.println("第1个盘从 " + firstTower + " => " + thirdTower);
}else {
show(plateNum-1, firstTower, thirdTower, secondTower);
System.out.println("第"+ plateNum +"个盘从 " + firstTower + " => " + thirdTower);
show(plateNum-1, secondTower, firstTower, thirdTower);
}
}
public static void main(String[] args) {
HanoiTower.show(1, 'a', 'b', 'c');
System.out.println("\n========================\n");
HanoiTower.show(2, 'a', 'b', 'c');
System.out.println("\n========================\n");
HanoiTower.show(3, 'a', 'b', 'c');
System.out.println("\n========================\n");
HanoiTower.show(4, 'a', 'b', 'c');
}
}

2. 动态规划
步骤
1、 问题拆分成多个小问题,不是相互独立;
2、 每个小问题的小解很可能基于其上一个小问题的解;
3、 方式:通过填表的方式进行逐步推进,获取最优解;
2.1 背包问题 - 固定容器的背包,如何能装入总价值最大的东西
背包问题分裂
1、 01背包-即不可装入重复的东西;
2、 无限背包-即可以装入重复的东西-【无限背包可以转01背包进行处理】;
2.1.1 01背包 - 不可装入重复的东西#
背包可容纳为4KG的东西 - 物品不可重复
| 物品 | 重量( KG ) | 价格 |
|---|---|---|
| 吉他 | 1 | 1500 |
| 音响 | 4 | 3000 |
| 电脑 | 3 | 2000 |
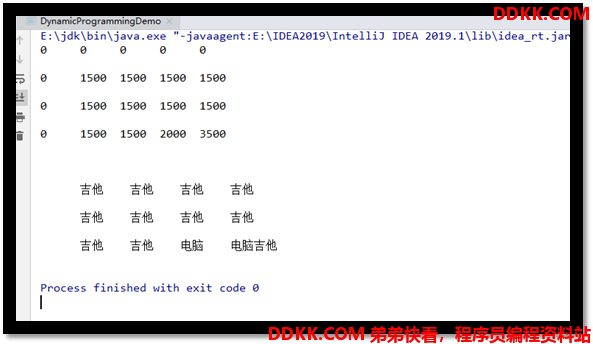
| 物品 \ 重量( KG ) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他 | 0 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 0 | 1500 | 1500 | 1500 | 3000 |
| 电脑 | 0 | 1500 | 1500 | 2000 | 2000+1500 |
填表思路 - 进行动态规划
# 表格中的行排表示当前列对应的最大容量所能装的东西( 从上到下的东西 )
# 如
(吉他,1KG):表示背包为1KG,物品有吉他 - 最大装入的价值是什么
(音响、1KG):表示背包为1KG,物品有吉他、音响 - 最大装入的价值是什么
(音响、4KG):表示背包为4KG,物品有吉他、音响 - 最大装入的价值是什么
(电脑,1KG):表示背包为1KG,物品有吉他、音响、电脑 - 最大的装入价值是什么
(电脑,3KG):表示背包为3KG,物品有吉他、音响、电脑 - 最大的装入价值是什么
package top.linruchang.algorithm.commonAlgorithms;
/**
* 动态规划案例
*
* @Classname DynamicProgrammingDemo
* @Description
* @Date 2022/4/17 11:21
* @Created by lrc
*/
public class DynamicProgrammingDemo {
int[][] value;
String[][] maxValueThings;
int[] prices;
int[] weights;
String[] thingsName;
DynamicProgrammingDemo() {
prices = new int[]{
1500, 300, 2000};
weights = new int[]{
1, 4, 3};
thingsName = new String[]{
"吉他", "音响", "电脑"};
maxValueThings = new String[4][5];
value = new int[4][5];
for (int i = 0; i < 4; i++) {
if (i == 0) {
for (int j = 0; j < 5; j++) {
value[i][j] = 0;
maxValueThings[i][j] = "";
}
}
value[i][0] = 0;
maxValueThings[i][0] = "";
}
}
public void dynamicMethod() {
for (int i = 1; i < 4; i++) {
for (int j = 1; j < 5; j++) {
//如果当前物品的重量大于列对应的重量,则直接取上一个空格的结果
if(weights[i-1] > j) {
value[i][j] = value[i-1][j];
maxValueThings[i][j] = maxValueThings[i-1][j];
//如果当前物品的重量小于等于列对应的重量,直接取上一个空格的结果与 当前物品+对应减少重量的空格结果
}else {
int lastCurrentPrice = value[i-1][j];
int currentCurrentPrice = prices[i-1] + value[i-1][j - weights[i-1]];
int maxValue = Math.max(lastCurrentPrice, currentCurrentPrice);
value[i][j] = maxValue;
if(maxValue == lastCurrentPrice) {
maxValueThings[i][j] = maxValueThings[i-1][j];
}else {
maxValueThings[i][j] = thingsName[i-1] + maxValueThings[i-1][j - weights[i-1]];
}
}
}
}
//打印表格的各个总价值
for(int i = 0; i<value.length; i++) {
for(int j = 0; j < value[i].length; j++) {
System.out.printf("%-5s ", value[i][j]);
}
System.out.println("\n");
}
//打印表格的每个对应的物品
for(int i = 0; i<maxValueThings.length; i++) {
for(int j = 0; j < maxValueThings[i].length; j++) {
System.out.printf("%-5s " , maxValueThings[i][j] );
}
System.out.println("\n");
}
}
public static void main(String[] args) {
DynamicProgrammingDemo dynamic = new DynamicProgrammingDemo();
dynamic.dynamicMethod();
}
}
3. KMP、暴力匹配算法
1. 解决模式串在文本串是否出现过,如果出现过,返回最早出现在文本串的位置
2. KMP思想: 通过一个next数组,保存模式串中前后最长公共子序列的长度,每次回溯时,通过next数组找到,前面匹配过的位置(index = index + (已匹配字符数 - next[i])),省去了大量的计算时间



next()数组例子
// next数值为:前缀=后缀 前缀的最大长度
// 需要查找的字符:ABCDABD
next[] 数组为 {
0, 0, 0, 0, 1, 2, 0 }
// 需要查找的字符:abadcababa
next[] 数组为 {
0, 0, 1, 0, 0, 1, 2, 3, 2, 3 }
// 遇到不匹配时,主字符串指针移动的下一步为
index = index + ( pattern匹配到的字符长度L - next[L-1] )
StringMatching.java
/**
* 暴力匹配字符串
*
* @Classname StringMatching
* @Description
* @Date 2022/4/17 16:29
* @Created by lrc
*/
public class StringMatching {
/* String matchedStr;
String pattern;
StringMatching(String matchedStr, String pattern) {
this.matchedStr = matchedStr;
this.pattern = pattern;
}
*/
public static int violentMatch(String matchedStr, String pattern) {
char[] matchedStrcChars = matchedStr.toCharArray();
char[] patternChars = pattern.toCharArray();
int index = 0;
while (index < matchedStr.length()) {
//如果主字符串剩余能被匹配的字符小于 被匹配的字符串长度,则直接退出
if (matchedStr.length() - index < pattern.length()) {
break;
}
int currentIndex = index;
int index2 = 0;
while (true) {
//匹配字符时,主字符串、被匹配字符串指针都向前移
if (matchedStrcChars[currentIndex] == patternChars[index2]) {
index2++;
currentIndex++;
} else {
//一旦不匹配时,被匹配字符串指针重新开始,主字符串为上次记录的位置下一个指针
index++;
index2 = 0;
break;
}
if (index2 == pattern.length()) {
return index;
}
}
}
return -1;
}
public static int kmpMatch(String matchedStr, String pattern) {
char[] matchedStrcChars = matchedStr.toCharArray();
char[] patternChars = pattern.toCharArray();
int[] next = getNext(pattern);
int index = 0;
while (index < matchedStr.length()) {
//如果主字符串剩余能被匹配的字符小于 被匹配的字符串长度,则直接退出
if (matchedStr.length() - index < pattern.length()) {
break;
}
int currentIndex = index;
int index2 = 0;
while (true) {
//匹配字符时,主字符串、被匹配字符串指针都向前移
if (matchedStrcChars[currentIndex] == patternChars[index2]) {
index2++;
currentIndex++;
} else {
//一旦不匹配时,被匹配字符串指针重新开始,主字符串为上次记录的位置下一个指针
//这里使用next数组进行移动主字符串得指针
//index = index + (已经匹配成功得pattern长度 - next对应得值)
if (next[index2] != 0) {
index += (index2 + 1) - next[index2];
} else {
index++;
}
index2 = 0;
break;
}
if (index2 == pattern.length()) {
return index;
}
}
}
return -1;
}
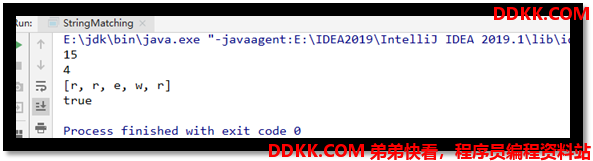
public static void main(String[] args) {
System.out.println(StringMatching.violentMatch("BBC ABCDAB ABCDABCDABDE", "ABCDABD"));
System.out.println(StringMatching.kmpMatch("BBC ABCDAB ABCDABCDABDE", "ABCDABD"));
System.out.println(Arrays.toString("rrewr".toCharArray()));
System.out.println("rrewr".toCharArray()[0] == "rrewr".toCharArray()[1]);
/* int[] next = getNext("abadcababa");
next = getNext("abadcababa");
System.out.println(Arrays.toString(next));*/
}
public static int[] getNext(String pattern) {
int[] next = new int[pattern.length()];
next[0] = 0;
for (int i = 1, j = 0; i < next.length; i++) {
//这步实在是看不太懂
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}
}
4. 贪心算法 - 解决集合覆盖问题
贪心算法:指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法
注意:能得到结果,但并不是最好的 - 例如下面的电台问题,能筛选到能覆盖所有地区的地台,但并不能保证这个电台组合是价钱最便宜的

思路
- 查找每个电台在需要覆盖地区集合S的覆盖数 - 并记录下来
- 扫描完所有电台的覆盖数 - 从中找到覆盖数最大的电台,并且记录该电台到集合A中
- 选中最大覆盖数的电台则将 该电台的覆盖地区 从 集合S中剔除
- 重复上述步骤,直到S的容量为0
- 集合A中的电台即可以覆盖所有地区

/**
* @Classname GreedyAlgorithm
* @Description
* @Date 2022/4/18 9:20
* @Created by lrc
*/
public class GreedyAlgorithm {
Map<String, Set<String>> broadcastingStation;
Set<String> coverageAreas;
GreedyAlgorithm(Map<String, Set<String>> broadcastingStation, HashSet<String> coverageAreas ) {
this.broadcastingStation = broadcastingStation;
this.coverageAreas = coverageAreas;
}
public ArrayList<String> getStation() {
// 电台需要覆盖的地区
HashSet<String> copyCoverageAreas = new HashSet<>(coverageAreas);
// 每个电台 所有地区 需要放入到这个集合进行跟copyCoverageAreas进行并集比较
HashSet<String> tempArea = new HashSet<>();
// 记录每次循环 每个电台的覆盖地区数
HashMap<String, Integer> coverageAreasNumStation = new HashMap<>();
// 记录哪个电台覆盖的地区最广
String maxKey = null;
// 每次循环,将上面的maxKey记录到这里面 - 结果返回
ArrayList<String> resultStation = new ArrayList<>(broadcastingStation.size());
// 如果并没有覆盖完所有地区,则再次循环
while(copyCoverageAreas.size() != 0) {
//获取电台
Set<String> stations = broadcastingStation.keySet();
Iterator<String> iterator = stations.iterator();
while(iterator.hasNext()) {
String station = iterator.next();
//将当前电台覆盖的地区放入临时集合
tempArea.addAll(broadcastingStation.get(station));
// tempArea copyCoverageAreas的并集 放入到 tempArea中
tempArea.retainAll(copyCoverageAreas);
// 记录当前电台覆盖的地区数,并放入coverageAreasNumStation记录
Integer overrideAreaNum = tempArea.size();
coverageAreasNumStation.put(station, overrideAreaNum);
if(maxKey == null || (coverageAreasNumStation.get(maxKey) < coverageAreasNumStation.get(station) )) {
maxKey = station;
}
tempArea.clear();
}
resultStation.add(maxKey);
// 选中最大的覆盖地区数,并将从broadcastingStation中剔除出来 - 等待下次循环
if(maxKey != null) {
copyCoverageAreas.removeAll(broadcastingStation.get(maxKey));
}
maxKey = null;
}
return resultStation;
}
public static void main(String[] args) {
//构造测试数据
Set<String> set1 = new HashSet<>();
set1.add("北京");
set1.add("上海");
set1.add("天津");
Set<String> set2 = new HashSet<>();
set2.add("广州");
set2.add("北京");
set2.add("深圳");
Set<String> set3 = new HashSet<>();
set3.add("成都");
set3.add("上海");
set3.add("杭州");
Set<String> set4 = new HashSet<>();
set4.add("天津");
set4.add("上海");
Set<String> set5 = new HashSet<>();
set5.add("杭州");
set5.add("大连");
Map<String, Set<String>> broadcastingStation = new HashMap<>();
broadcastingStation.put("k1", set1);
broadcastingStation.put("k2", set2);
broadcastingStation.put("k3", set3);
broadcastingStation.put("k4", set4);
broadcastingStation.put("k5", set5);
String[] areas = {
"北京", "上海", "天津", "广州", "深圳", "成都", "上海", "杭州", "大连"};
HashSet<String> coverageAreas = new HashSet<>(Arrays.asList(areas));
GreedyAlgorithm greedyAlgorithm = new GreedyAlgorithm(broadcastingStation, coverageAreas);
//查看结果
System.out.println(greedyAlgorithm.getStation());
}
}
5. 图
5.1 最小生成树(所有结点都有路可走) - Minimum Spanning Tree
概念
- 从一个带权的无向连通图 - 生成一颗树 - 边上权的总和为最小
最小生成树特点
1、 N个顶点、N-1条边;
2、 必须包含全部顶点;
3、 生成树的边全部来自提供的无向连通图中;
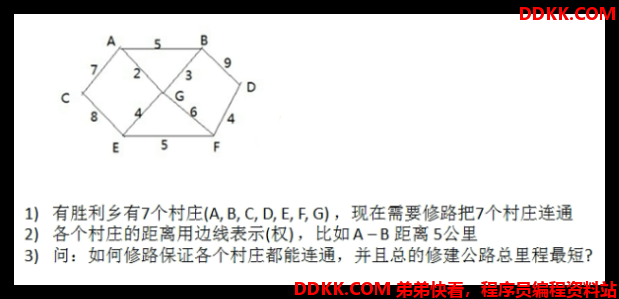
5.1.1 普里姆算法#
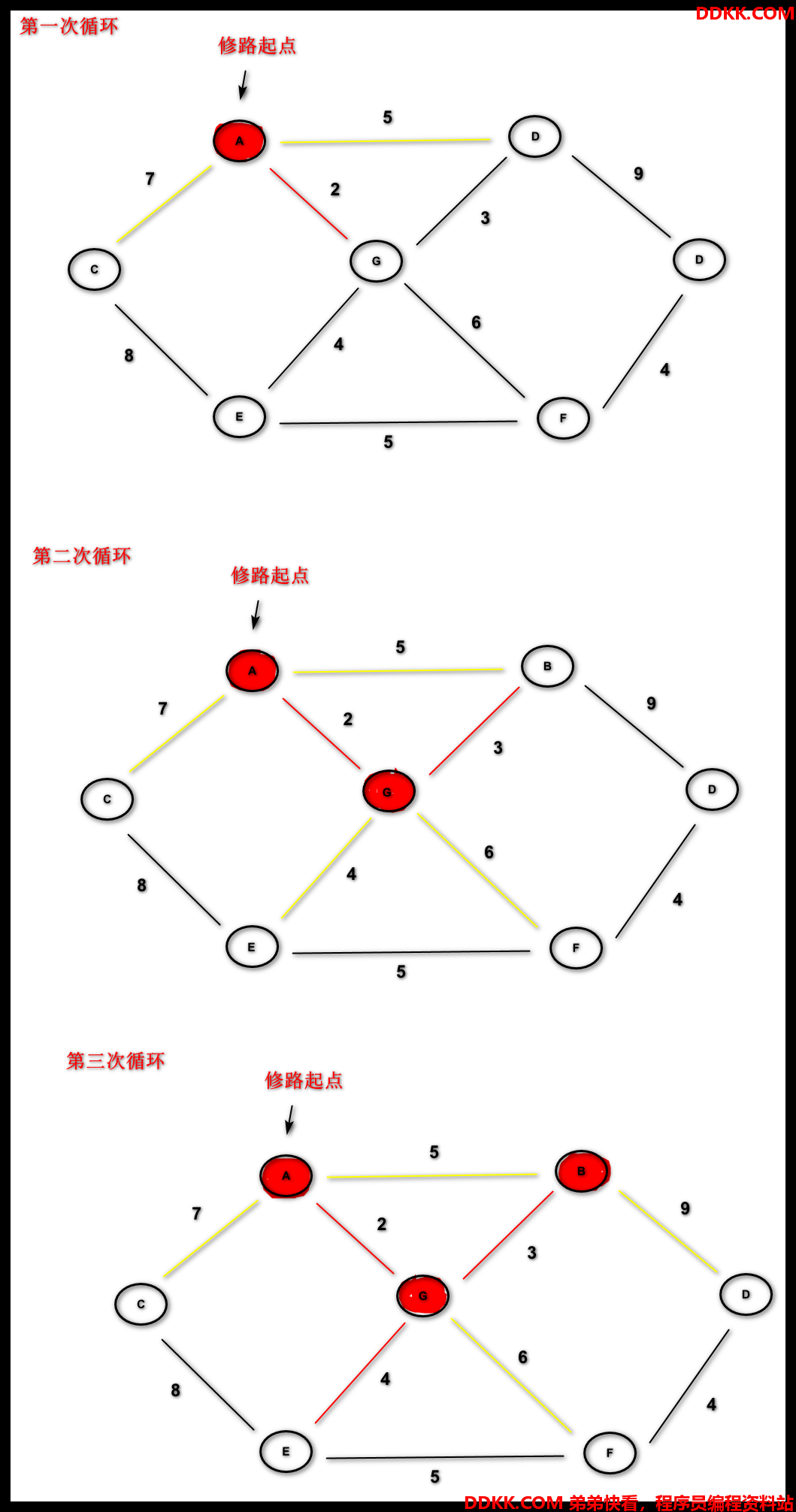
思路:
- 选取某个结点为起点V,
- 将该结点放入一个容器中,
- 比较以该容器中的结点为边,
- 比较得到最小的边,即为需要连接的边,并将结点放入容器中
- 循环2,3,4 — 直到容器中包括所有结点**
只画了前三次循环的步骤 - 后面几次循环就不画了,实在太难画了
/**
* @Classname PrimAlgorithm
* @Description
* @Date 2022/4/18 15:30
* @Created by lrc
*/
public class PrimAlgorithm {
public static void main(String[] args) {
//1, 结点信息
String[] vertexs = {
"A", "B", "C", "D", "E", "F", "G"};
Integer n = vertexs.length;
// 2. 创建带5个结点的无序带权图
UndirectedWeightGraph graph = new UndirectedWeightGraph(n);
// 3. 添加结点
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
// 4. 添加结点之间的权值 - 这里的权值>0表示两结点之间可以进行修路且修路的长度 =0表示不可以进行修路
graph.insertWeight(0, 1, 5);
graph.insertWeight(0, 2, 7);
graph.insertWeight(0, 6, 2);
graph.insertWeight(1, 6, 3);
graph.insertWeight(1, 3, 9);
graph.insertWeight(2, 4, 8);
graph.insertWeight(3, 5, 4);
graph.insertWeight(4, 6, 4);
graph.insertWeight(4, 5, 5);
graph.insertWeight(5, 6, 6);
// 5. 显示图的矩阵
//System.out.println(graph.getGraph());
graph.showGrpah();
PrimAlgorithm primAlgorithm = new PrimAlgorithm();
primAlgorithm.prim(graph , 0);
}
/**
*
* @param graph 带有权值的无向图
* @param n 从哪个结点开始修路 - A -> 0, B -> 1等等
*/
public void prim(UndirectedWeightGraph graph, int n) {
//获取结点的数量
Integer vertexNum = graph.getVertexsNum();
//标记是否选中该结点
boolean[] visted = new boolean[vertexNum];
//全部结点都标记为fasle
for(int i = 0; i<vertexNum; i++) {
visted[i] = false;
}
//存储准备修路的结点
ArrayList<Integer> vistedVertex = new ArrayList<>(vertexNum);
vistedVertex.add(n);
//修路长度
int sumLength = 0;
while(vistedVertex.size() < vertexNum) {
//记录下一次修的路径
int firstVertext = -1;
int secondVertext = -1;
//标记当前结点的边的最短路径
Integer minWeight = 0;
// 获取已经准备修路的其他最小边
Integer size = vistedVertex.size();
for(int i = 0; i< size; i++) {
for(int j = 0; j<vertexNum; j++) {
if(vistedVertex.contains(j) == false) {
Integer curWeight = graph.getWeight(vistedVertex.get(i), j);
if((minWeight == 0 && curWeight != 0) || (curWeight != 0 && minWeight > curWeight)) {
minWeight = curWeight;
firstVertext = vistedVertex.get(i);
secondVertext = j;
}
}
}
}
if(secondVertext != -1) {
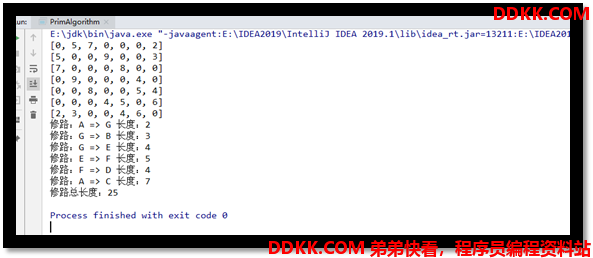
System.out.printf("修路:%s => %s 长度:%s\n",graph.getVertex(firstVertext), graph.getVertex(secondVertext), minWeight);
sumLength = sumLength + minWeight;
vistedVertex.add(secondVertext);
}
}
System.out.println("修路总长度:" + sumLength);
}
}
//无向带权图
class UndirectedWeightGraph {
//存储结点
ArrayList<String> vertexs;
// 存储结点之间的权值 - 结点之间的关系 -- 矩阵
int[][] edges;
// 存储图中边的个数
int numOfEdges;
//初始化 - 结点个数
UndirectedWeightGraph(int vertexsNum) {
this.vertexs = new ArrayList<>(vertexsNum);
this.edges = new int[vertexsNum][vertexsNum];
this.numOfEdges = 0;
}
//获取结点
public String getVertex(int n) {
return vertexs.get(n);
}
//获取边的个数
public int getNumOfEdges() {
return numOfEdges;
}
//获取结点个数
public int getVertexsNum() {
return this.vertexs.size();
}
//获取结点根据索引序号
public String getVertexByIndex(int index) {
return vertexs.get(index);
}
//添加新结点
public void insertVertex(String vertex) {
this.vertexs.add(vertex);
}
//获取两结点之间的边的权值 "A结点表示0" "B节点表示1"
public int getWeight(int firstVertex, int secondVertext) {
return edges[firstVertex][secondVertext];
}
//获取矩阵 - 即把数组Edges权值图打印出来
public String getGraph() {
return Arrays.deepToString(edges);
}
//显示矩阵
public void showGrpah() {
for (int[] edgeWeight : edges) {
System.out.println(Arrays.toString(edgeWeight));
}
}
//添加结点之间的关系 - 即权值 - 因为无向图的关系必须赋值数组中两个元素相同的权值
public void insertWeight(int firstVertex, int secondVertext, int weight) {
edges[firstVertex][secondVertext] = weight;
edges[secondVertext][firstVertex] = weight;
numOfEdges++;
}
}
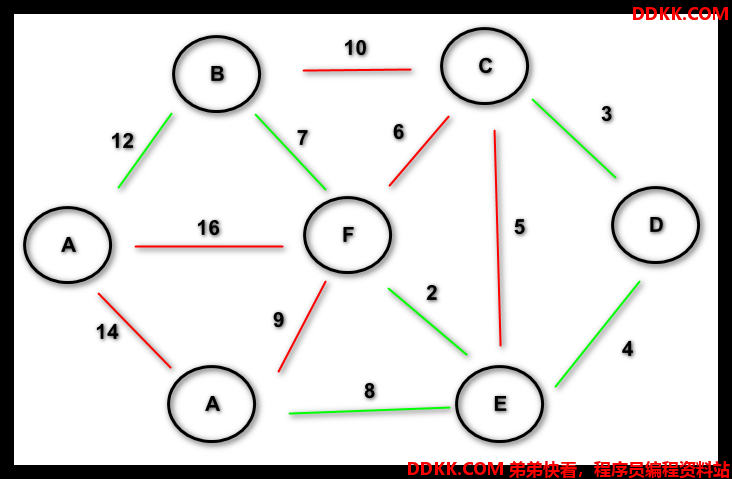
5.1.2 克鲁斯卡尔算法#
- 思想:
-
- 将所有边按权值从小到大排列
-
- 逐一加入上述的边,每加入一次需要验证是否构成回路,构成回路则剔除该边
-
- 遍历完①步骤所有边 - 筛选剩下的边即是最小生成树
绿线即是最小生成树
KruskalAlgorithm.java
/**
* @Classname KruskalAlgorithm
* @Description
* @Date 2022/4/18 18:49
* @Created by lrc
*/
public class KruskalAlgorithm {
public static void main(String[] args) {
//1, 结点信息
String[] vertexs = {
"A", "B", "C", "D", "E", "F", "G"};
Integer n = vertexs.length;
// 2. 创建带5个结点的无序带权图
MyGraph graph = new MyGraph(n);
// 3. 添加结点
for (String vertex : vertexs) {
graph.insertVertex(vertex);
}
// 4. 添加结点之间的权值 - 这里的权值>0表示两结点之间可以进行修路且修路的长度 =0表示不可以进行修路
graph.insertWeight(0, 1, 12);
graph.insertWeight(0, 5, 16);
graph.insertWeight(0, 6, 14);
graph.insertWeight(1, 5, 7);
graph.insertWeight(1, 2, 10);
graph.insertWeight(2, 5, 6);
graph.insertWeight(2, 3, 3);
graph.insertWeight(2, 4, 5);
graph.insertWeight(3, 4, 4);
graph.insertWeight(4, 5, 2);
graph.insertWeight(4, 6, 8);
graph.insertWeight(5, 6, 9);
// 5. 显示图的矩阵
//System.out.println(graph.getGraph());
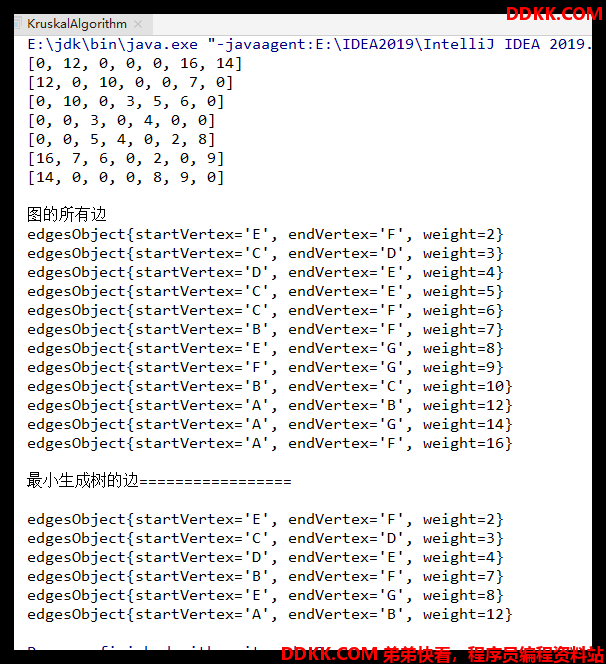
graph.showGrpah();
// 6. 最小生成树的边
List<MyGraph.EdgeObject> miniSpanningTree = kruskal(graph);
System.out.println("\n最小生成树的边=================\n");
for(MyGraph.EdgeObject edge : miniSpanningTree) {
System.out.println(edge);
}
}
public static List<MyGraph.EdgeObject> kruskal(MyGraph graph) {
//排序图所有边的权值 - 升序排列
List<MyGraph.EdgeObject> edges = graph.getEdgeObjects();
Collections.sort(edges);
//图中所有边升序后的情况
System.out.println("\n图的所有边");
for(MyGraph.EdgeObject edge : edges) {
System.out.println(edge);
}
//动态变化的最小生成树 - 每个结点的终点坐标
int[] ends = new int[graph.getVertexsNum()];
//最小生成树的边
List<MyGraph.EdgeObject> miniSpanningTree = new ArrayList<>();
//遍历图的所有边,找到符合最小生成树的边
for(MyGraph.EdgeObject edge : edges) {
// 获取当前边的 两结点的坐标
int startVertxIndex = edge.startVertexIndex;
int endVertxIndex = edge.endVertexIndex;
// 获取这两个结点的终点坐标
int endVertex1 = endVertex(ends, startVertxIndex);
int endVertex2 = endVertex(ends, endVertxIndex);
// 两个两结点的终点坐标不一致,说明符合最小生成树的边
if(endVertex1 != endVertex2) {
ends[endVertex1] = endVertex2;
miniSpanningTree.add(edge);
}
}
return miniSpanningTree;
}
//这步实在看不懂 - 有点牛逼 - 利用结点的传递性进行赋终点坐标
public static int endVertex(int[] ends, int vertextIndex) {
while(ends[vertextIndex] != 0) {
vertextIndex = ends[vertextIndex];
}
return vertextIndex;
}
}
//无向带权图
class MyGraph {
//存储结点
ArrayList<String> vertexs;
// 存储结点之间的权值 - 结点之间的关系 -- 矩阵
int[][] edges;
// 存储图中边的个数
int numOfEdges;
List<EdgeObject> edgeObjects ;
//初始化 - 结点个数
MyGraph(int vertexsNum) {
this.vertexs = new ArrayList<>(vertexsNum);
this.edges = new int[vertexsNum][vertexsNum];
this.numOfEdges = 0;
this.edgeObjects = new ArrayList<>();
}
// 图的边对象
protected class EdgeObject implements Comparable<EdgeObject> {
//结点名字
String startVertex;
//结点索引
Integer startVertexIndex;
String endVertex;
Integer endVertexIndex;
Integer weight;
@Override
public String toString() {
return "edgesObject{" +
"startVertex='" + startVertex + '\'' +
", endVertex='" + endVertex + '\'' +
", weight=" + weight +
'}';
}
@Override
public int compareTo(EdgeObject edgesObject) {
return this.weight - edgesObject.weight;
}
}
//获取结点
public String getVertex(int n) {
return vertexs.get(n);
}
public List<EdgeObject> getEdgeObjects() {
return this.edgeObjects;
}
//获取边的个数
public int getNumOfEdges() {
return numOfEdges;
}
//获取结点个数
public int getVertexsNum() {
return this.vertexs.size();
}
//获取结点根据索引序号
public String getVertexByIndex(int index) {
return vertexs.get(index);
}
//添加新结点
public void insertVertex(String vertex) {
this.vertexs.add(vertex);
}
//获取两结点之间的边的权值 "A结点表示0" "B节点表示1"
public int getWeight(int firstVertex, int secondVertext) {
return edges[firstVertex][secondVertext];
}
//获取矩阵 - 即把数组Edges权值图打印出来
public String getGraph() {
return Arrays.deepToString(edges);
}
//显示矩阵
public void showGrpah() {
for (int[] edgeWeight : edges) {
System.out.println(Arrays.toString(edgeWeight));
}
}
//添加结点之间的关系 - 即权值 - 因为无向图的关系必须赋值数组中两个元素相同的权值
public void insertWeight(int firstVertex, int secondVertext, int weight) {
edges[firstVertex][secondVertext] = weight;
edges[secondVertext][firstVertex] = weight;
numOfEdges++;
EdgeObject edgesObject = new EdgeObject();
edgesObject.startVertex = vertexs.get(firstVertex);
edgesObject.startVertexIndex = firstVertex;
edgesObject.endVertex = vertexs.get(secondVertext);
edgesObject.endVertexIndex = secondVertext;
edgesObject.weight = weight;
edgeObjects.add(edgesObject);
}
}