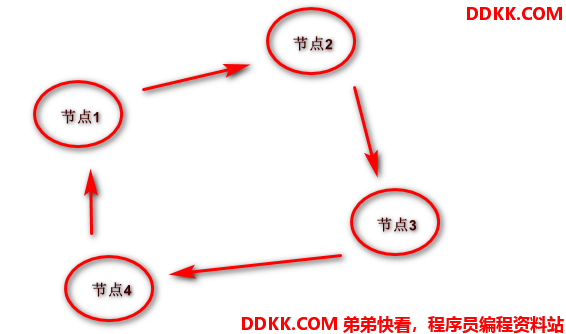
单向环形链表 - 无头指针
测试类
class Student2 {
private int id;
private String name;
public Student2(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Student2 [id=" + id + ", name=" + name + "]";
}
}
增加元素、遍历链表
代码实现 - 增加元素
class SingleCircularLinkedList<T> {
private Node<T> firstNode = null;
// 向尾部增加一个节点
public void add(T t) {
// 1.将添加的元素封装成节点
Node<T> newNode = new Node<T>(t);
// 2.1 如果链表为空则直接单元素环形链表
if (firstNode == null) {
firstNode = newNode;
firstNode.next = firstNode;
return;
// 2.2 如果链表中有一个元素
} else if (firstNode == firstNode.next) {
firstNode.next = newNode;
newNode.next = firstNode;
return;
// 2.3 链表中存在2个或以上的元素
} else {
// 当前遍历到的节点
Node<T> temp = firstNode;
// 遍历获取到最后一个节点
while (temp.next != firstNode) {
temp = temp.next;
}
temp.next = newNode;
newNode.next = firstNode;
}
}
private class Node<T> {
T date;
Node<T> next;
Node(T date) {
this.date = date;
}
@Override
public String toString() {
return date.toString();
}
}
}
代码实现 - 遍历节点
@Override
public String toString() {
// 头节点为null
if (firstNode == null) {
return null;
}
StringBuilder sb = new StringBuilder();
// 遍历到的当前节点
Node<T> temp = firstNode;
while (true) {
sb.append(temp.toString() + "\n");
if (temp.next == firstNode) {
break;
}
temp = temp.next;
}
sb.delete(sb.lastIndexOf("\n"), sb.length());
return sb.toString();
}
测试代码
public static void main(String[] args) {
Student2 stu1 = new Student2(1, "lrc");
Student2 stu2 = new Student2(2, "glw");
Student2 stu3 = new Student2(3, "yte");
SingleCircularLinkedList<Student2> scll = new SingleCircularLinkedList<Student2>();
scll.add(stu1);
scll.add(stu2);
scll.add(stu3);
System.out.println(scll);
}
测试结果
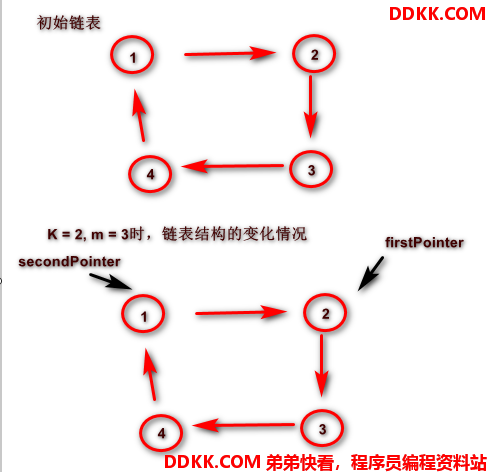
约瑟夫出队 – 需改变链表结构
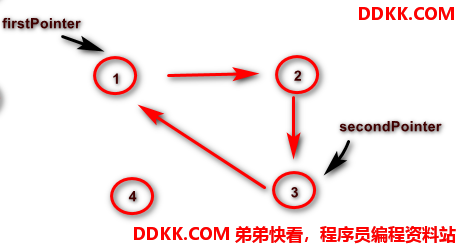
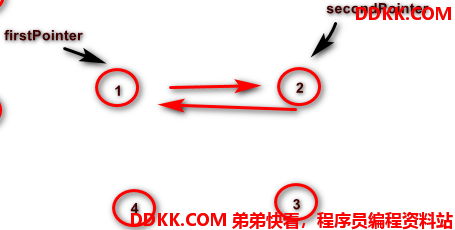
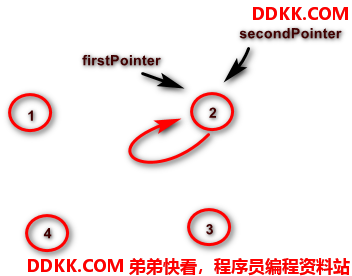
代码实现
/**
*
* @Description
* @param k 开始从第几个节点开始报数
* @param m 每次报数起,数多少次
*/
public void JosephOut(int k, int m) {
// 1. 链表必须有元素
if(length() == 0) {
System.out.println("链表中无元素");
return;
// 2. 开始从第几个节点数,必须小于 链表的长度
}else if(length() < k || k < 0 ) {
System.out.println("参数K不符合输入要求");
return;
}else {
// 3.1 需要两个指针, -个是准备出队的那个节点指针,另一个是firstPointer节点后面那个节点
Node<T> firstPointer = firstNode;
Node<T> secondPointer = firstNode;
// 3.2 需要到从第K个节点开始遍历出队的指针
for(int i = 1; i < k; i++) {
firstPointer = firstPointer.next;
if(i >= 2) {
secondPointer = secondPointer.next;
}
}
// 3.3 需要一个标志位来判断 firstPointer.secondPointer节点是否是前后关系
boolean flag = false;
// 3.4 开始遍历出队
while(true) {
// 3.4.1 有元素出队后,需要重新遍历查找下一个出队的节点 - 移动m-1次
for(int i = 0; i<m-1; i++) {
if(k == 1 && i == 0 && flag == false) {
firstPointer = firstPointer.next;
flag = true;
continue;
}else {
firstPointer = firstPointer.next;
secondPointer = secondPointer.next;
}
}
// 3.4.2 打印出队元素,并且调整链表中的节点
System.out.println(firstPointer);
firstPointer = firstPointer.next;
secondPointer.next = firstPointer;
// 如果最后整个单向环形链表只有一个元素,则直接退出循环
if(secondPointer.next == secondPointer) {
break;
}
}
// 4. 打印链表最后一个节点
System.out.println(secondPointer);
// 5. 将链表置空
firstNode = null;
}
}
约瑟夫问题

代码测试
public static void main(String[] args) {
// 1. 定义、初始化6个人
Student2 stu1 = new Student2(1, "lrc");
Student2 stu2 = new Student2(2, "glw");
Student2 stu3 = new Student2(3, "yte");
Student2 stu4 = new Student2(4, "erw");
Student2 stu5 = new Student2(5, "ghb");
Student2 stu6 = new Student2(6, "fgh");
SingleCircularLinkedList<Student2> scll = new SingleCircularLinkedList<Student2>();
// 2. 将6个人添加到链表里面
scll.add(stu1);
scll.add(stu2);
scll.add(stu3);
scll.add(stu4);
scll.add(stu5);
scll.add(stu6);
System.out.println("人数N = " + scll.length());
int M = 5; int K = 1;
// 3. 约瑟夫出列
scll.JosephOut(K, M);
}
运行结果