树
不限制每个节点的子节点个数
专业术语
高度、深度:树的层数
节点:每个元素代表一个节点
根节点:无父亲的节点
子节点:父节点的儿子
叶子:无儿子的节点
度
节点度:当前节点的子节点个数
树的度:树中最大的节点度
平衡因子:左右子树的高度差
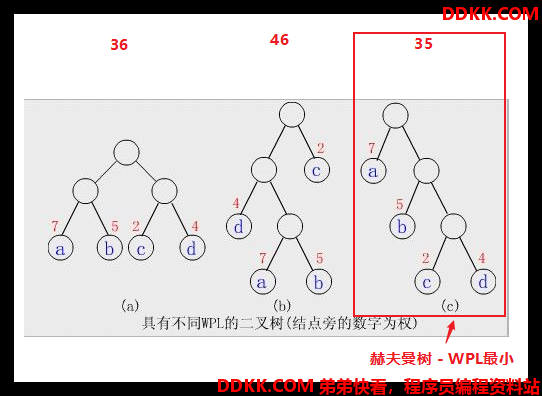
结点带权路径长度:结点权 * (根结点到当前的结点路径的长度)
树的带权路径长度(WPL):叶子结点的带权路径长度和
1.1 二叉树
每个元素的子节点个数最多为2,所以有左右节点之分
1.1.1 满二叉树
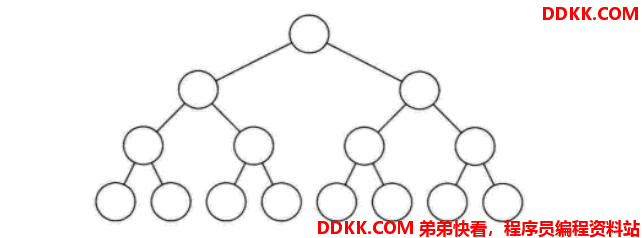
概念:除了最后一层,所有层的节点的子节点个数都是2
节点数n = 2^(h-1) → h为树的深度
1.1.2 完全二叉树
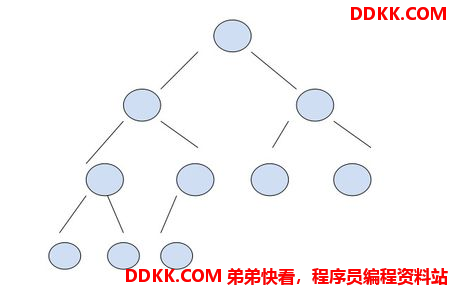
满足下列条件:
-
最后一层元素必须左到右的元素紧凑相连
-
抹去最后一层节点,则该树为满二叉树
1.1.3 堆
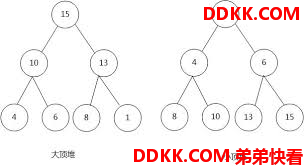
概念:
-
大顶堆: 节点值 >= 左右节点值的完全二叉树
-
小顶堆: 节点值 <= 左右节点值的完全二叉树
1.1.4 斜树
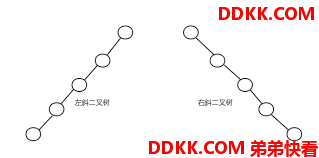
概念:所有父节点的子节点只有左节点( 右节点 )
1.1.5 二叉查找( 排序 )树
该树中序遍历元素一定是从小到大排序的
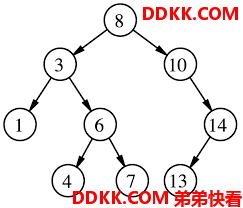
满足下列条件
1、 左节点小于父节点;
2、 右节点大于父节点;
3、 所有节点的左右子树都需满足1、2条件;
1.1.6 平衡二叉树 - AVL树 - 各节点平衡因子<=1
左右子树高度相差不超过1
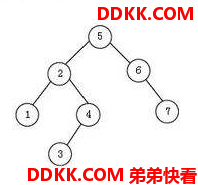
满足下列条件:
1、 节点数=0或者左右子树的深度差<=1;
2、 树中每个节点的需要满足1条件;
1.1.7 赫夫曼树(最优二叉树) - 树带权路径长度最小的树(相同数量的相同权值叶子节点)
1.1.0 遍历
方式
前序遍历:根 → 左子树 → 右子树
中序遍历:左子树 → 根 → 右子树
后序遍历:左子数 → 右子树 → 根
层次遍历:顶层开始琢层进行遍历,每层从左到右遍历
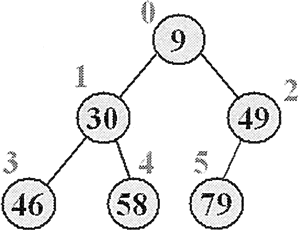
图中的完全二叉树四大遍历形式的结果:
1、 *前序遍历:*93046584979;
2、 *中序遍历:*46305897949;
3、 *后续遍历:*46583079499;
4、 *层次遍历:*93049465879;