1、基本思想
归并排序利用归并的思想实现排序,采用经典的分治策略,分阶段把问题拆分成一个个小的问题,然后递归秋节;治阶段则将分的阶段得到的答案进行“修补”在一起。即分而治之。
2、图解
首先从整体上了解归并排序,可以看出,分的阶段先把序列拆封成多个子序列,治的阶段则是把子序列依此合并,最后得到一个排序好的序列。
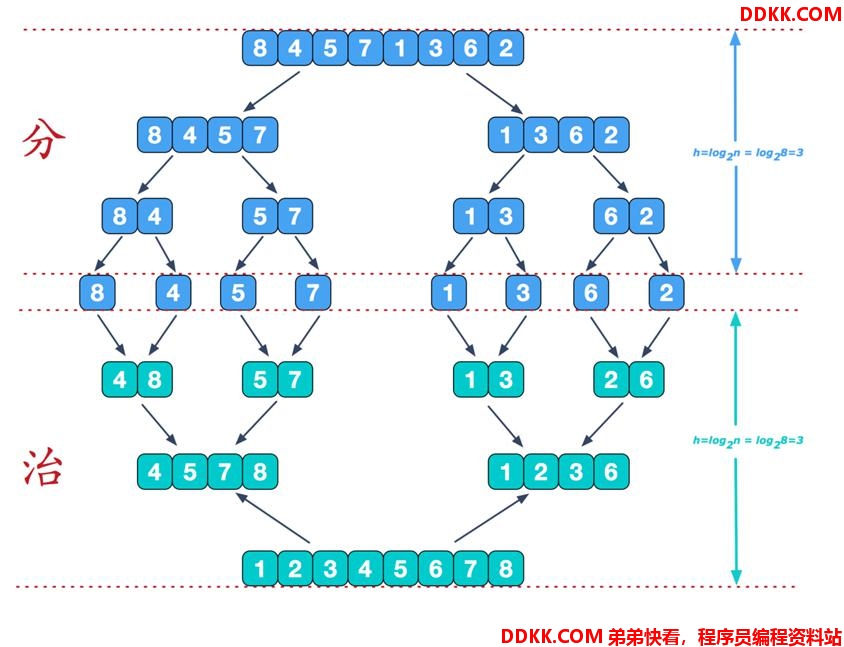
分阶段很明显,就是直接左右拆分,而治的阶段则有一个特定的归并操作,这也是归并排序名称的由来。
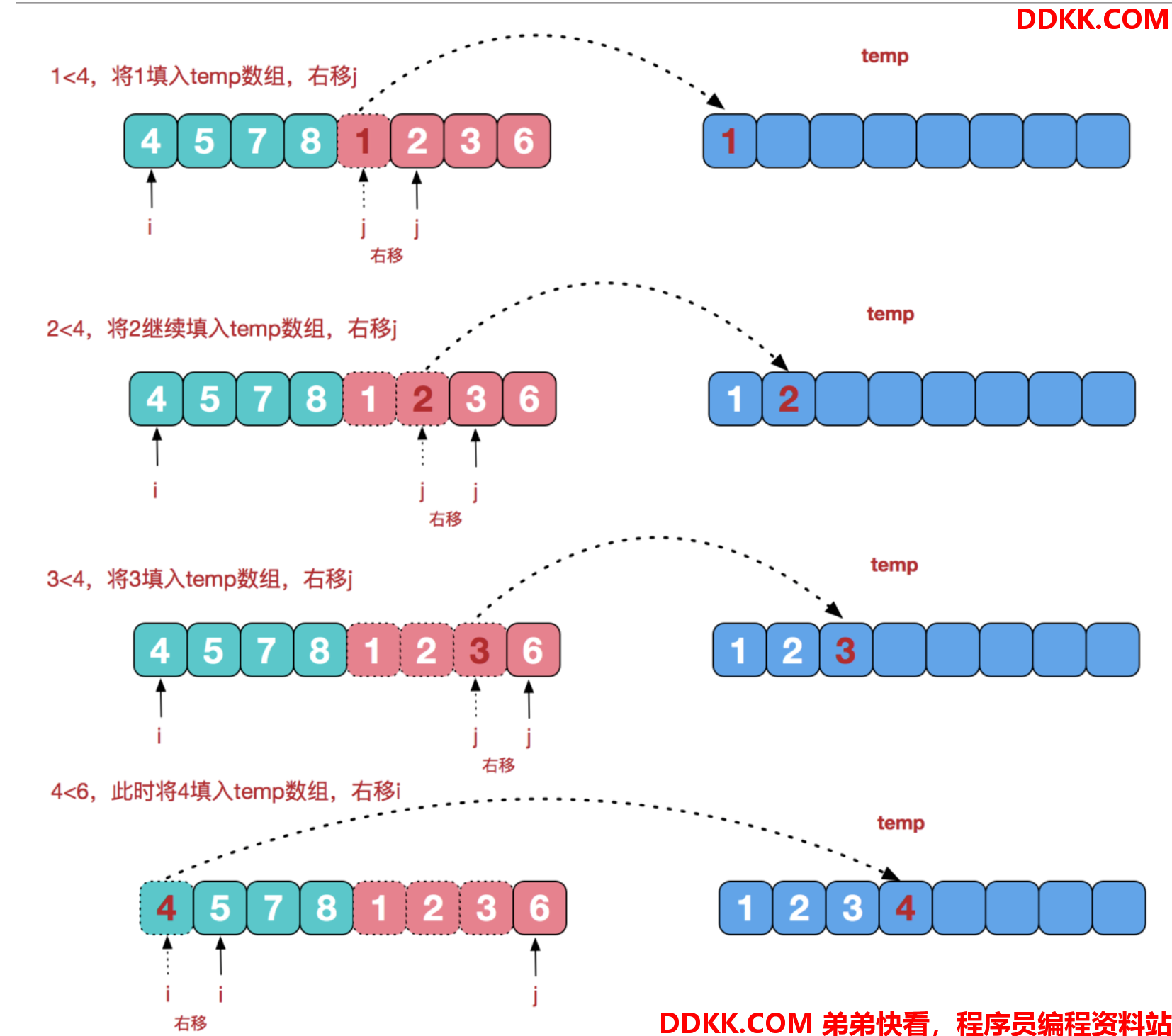
假设有两个子序列{4,5,7,8}和{1,2,3,6}要进行归并操作,归并过程如下:
3、代码实现
package cn.klb.datastructures.sort;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 实现数组的归并排序
* @Date: Create in 2023/4/5 12:33
* @Modified By:
*/
public class Merge {
public static void sort(int[] arr) {
int left = 0; // 最开始左指针为最左边
int right = arr.length - 1; // 最开始右指针为最右边
doSort(arr, left, right, new int[arr.length]);
}
private static void doSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
// 左右递归其实就是不断确定左序列的index和右序列的index
// 左右序列操作的本质上还是那一个数组,所以要不断确定操作的index
// 向左递归
doSort(arr, left, (left + right) / 2, temp);
// 向右递归
doSort(arr, (left + right) / 2 + 1, right, temp);
// 归并操作
merge(arr, left, right, temp);
}
}
/**
* 执行归并操作
*
* @param arr 数组
* @param left 左边子数组第一个元素下标
* @param right 右边子数组的最后一个元素下标
* @param temp 中间临时存放元素用的数组
*/
private static void merge(int[] arr, int left, int right, int[] temp) {
int i = left; // 左边有序列表初始索引
int j = (left + right) / 2 + 1; // 右边有序列表初始索引
int t = 0; // 临时数组索引
while (i <= (left + right) / 2 && j <= right) {
if (arr[i] <= arr[j]) {
// 如果左边序列的值小于右边,则把小的值存入temp数组
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
// 如果一边索引走完了,另一边还有剩余的元素,则直接放到temp里面
while (i <= (left + right) / 2) {
// 左边还有剩余元素
temp[t++] = arr[i++];
}
while (j <= right) {
// 右边还有剩余元素
temp[t++] = arr[j++];
}
// 把归并好的元素拷贝到arr
t = 0; // 重置temp索引
int l = left;
while (l <= right) {
arr[l++] = temp[t++];
}
}
}
4、时间复杂度
假设两个序列元素个数之和为n,执行归并操作,不考虑比较次数,光是把两个序列的元素拷贝到临时数组,就得进行n次操作。对于n=1归并排序所用时间记为1,则对n个数序列进行归并排序所耗时间等于两个大小为n/2的归并排序时间之和。
因此有:T(1) = 1,T(n) = 2T(n/2)+n。
联立两个式子,解得T(n) = nlogn + n = O(nlogn)。
5、稳定性
分析代码:
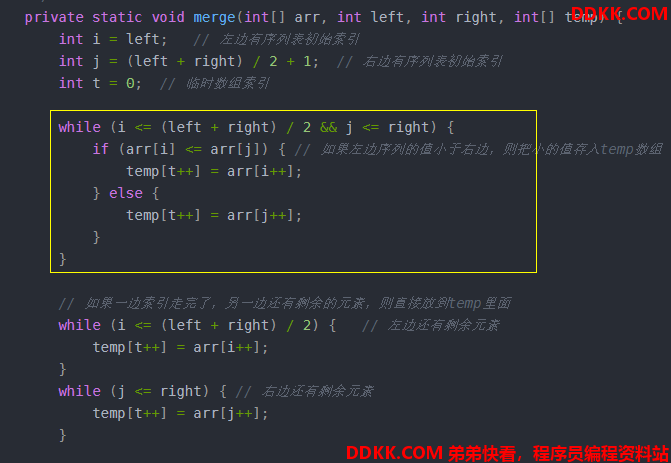
这个if判断条件可以决定是不是稳定,如果是<=,那么相同数字的前后关系不会改变;如果是<,则遇到相同数字时,会先把右边子序列的该数字先放到临时数组,破坏相同数字的前后关系,变得不稳定。
既然可以通过代码修改变得稳定,那么归并排序就是稳定的。完全没办法变成稳定的才是不稳定的算法。
6、测试
package cn.klb.test.datastructurestest;
import cn.klb.datastructures.sort.*;
import org.junit.Test;
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 排序测试
* @Date: Create in 2023/4/3 21:32
* @Modified By:
*/
public class SotrTest {
@Test
public void testMerge(){
int[] arr = new int[80000000];
for (int i = 0; i < 80000000; i++) {
arr[i] = (int) (Math.random() * 80000000);
}
SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
Date date1 = new Date();
System.out.println("-----" + sdf.format(date1) + "-----");
//System.out.println(Arrays.toString(arr));
Merge.sort(arr);
Date date2 = new Date();
System.out.println("-----" + sdf.format(date2) + "-----");
//System.out.println(Arrays.toString(arr));
// 8000万的随机数据进行归并排序,我的电脑花了大约15秒
}
}