1、树的概念
1.1 为什么需要树这种数据结构
数组存储的特点是查询快、增删慢。
链式存储的特点是查询慢、增删快。
而树的存储能够提高数据的存储和读取效率。比如利用二叉排序树,既可以保证数据的检索速度,同时也可以保证数据的插入、删除、修改的速度。
1.2 树的常用术语
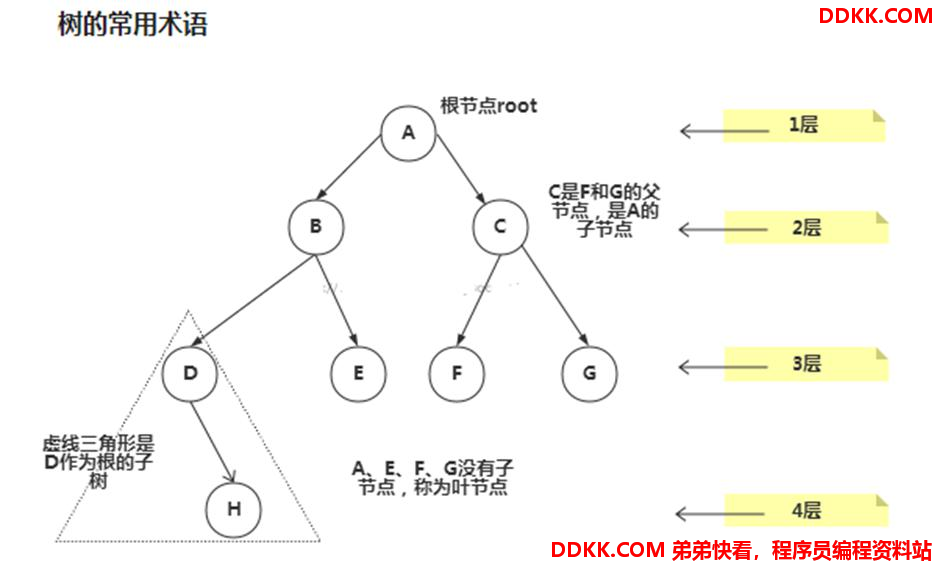
结点:也称为节点,就是树的每一个元素;
根结点:树最顶端的那个结点;
父结点:如图,B和C的父结点是A;
子结点:如图,A的子结点是B和C;
叶子结点:没有子结点的结点,如图的H、E、F和G;
结点的权:也就是结点的值;
路径:结点之间的箭头;
层:如图所示;
子树:每个结点加上它的子结点构成子树;
树的高度:即多少层;
森林:多颗子树构成森林。
2、二叉树
2.1 二叉树的基本概念
树的种类有很多,每个结点最多只能有两个子结点的形式称为二叉树。二叉树的子结点分为左结点和右结点。
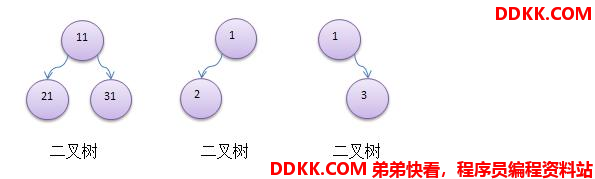
如果二叉树的所有叶子结点都在最后一层,且结点总数为 2^n-1,n为层数,则称为满二叉树。
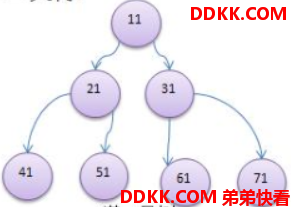
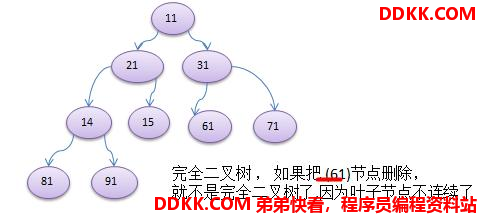
如果二叉树的所有叶子结点都在最后一层或者倒数第二层,而且最后一层的叶子结点在左边连续,倒数第二层的叶子结点在右边连续,则称为完全二叉树。
2.3 二叉树的代码实现
2.3.1 定义一个结点类:
package cn.klb.datastructures.tree;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 二叉树结点类
* @Date: Create in 2023/4/10 16:06
* @Modified By:
*/
public class Node {
public int id;
public String data;
public Node left;
public Node right;
public Node(int id,String data){
this.id = id;
this.data = data;
}
@Override
public String toString() {
return "Node{" +
"id=" + id +
", data='" + data + '\'' +
'}';
}
}
2.3.2 定义二叉树并实现添加方法:
前序遍历:先输出父结点,再遍历依次遍历左子树、右子树;
package cn.klb.datastructures.tree;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 二叉树
* @Date: Create in 2023/4/10 16:10
* @Modified By:
*/
public class BinaryTree {
public Node root; // 二叉树根节点
/**
* 添加结点
*
* @param node
*/
public void add(Node node) {
if (root == null) {
root = node;
} else {
Node temp = root;
while (true) {
if (node.id < temp.id) {
if (temp.left != null) {
temp = temp.left;
} else {
temp.left = node;
break;
}
} else if (temp.id < node.id) {
//
if (temp.right != null) {
temp = temp.right;
} else {
temp.right = node;
break;
}
}
}
}
}
}
2.3.3 二叉树的前序遍历
前序遍历:先输出父结点,再遍历左子树,最后遍历右子树;
/**
* 前序遍历
*/
public void preorderTraversal() {
doPreoderTraversal(root);
}
/**
* 前序遍历递归执行
*
* @param node
*/
private void doPreoderTraversal(Node node) {
System.out.println(node);
// 向左递归
if (node.left != null) {
doPreoderTraversal(node.left);
}
// 向右递归
if (node.right != null) {
doPreoderTraversal(node.right);
}
}
2.3.4 二叉树的中序遍历
中序遍历:先遍历左子树,然后输出父结点,最后遍历右子树;
/**
* 中序遍历
*/
public void inorderTraversal() {
doInorderTraversal(root);
}
/**
* 中序遍历递归执行
*
* @param node
*/
private void doInorderTraversal(Node node) {
// 向左递归
if (node.left != null) {
doInorderTraversal(node.left);
}
System.out.println(node);
// 向右递归
if (node.right != null) {
doInorderTraversal(node.right);
}
}
2.3.5 二叉树的后序遍历
后序遍历:先遍历左子树,然后遍历右子树,最后输出父结点;
/**
* 后序遍历
*/
public void postorderTraversal() {
doPostorderTraversal(root);
}
/**
* 后序遍历递归执行
*
* @param node
*/
private void doPostorderTraversal(Node node) {
// 向左递归
if (node.left != null) {
doPostorderTraversal(node.left);
}
// 向右递归
if (node.right != null) {
doPostorderTraversal(node.right);
}
System.out.println(node);
}
总结:看父结点在什么时候输出就确定是前序、中序还是后续。
2.3.6 二叉树查找指定结点
2.3.6.1 前序查找
/**
* 根据id查找对应结点,使用前序遍历法
*
* @param id
* @return
*/
public Node preoderGet(int id) {
return doPreoderGet(root, id);
}
private Node doPreoderGet(Node node, int id) {
if (node.id == id) {
// 如果当前结点就是要找的结点,则直接返回
return node;
}
Node temp = null;
if (node.left != null) {
// 当前结点不是要找的结点,则判断左节点是不是要找的结点
temp = doPreoderGet(node.left, id);
}
if (temp != null) {
// temp != null,表示已经找到结点,直接返回
return temp;
}
if (node.right != null) {
temp = doPreoderGet(node.right, id);
}
return temp;
}
2.3.6.2 中序查找
/**
* 根据id找结点,使用中序遍历
*
* @param id
* @return
*/
public Node inoderGet(int id) {
return doInoderGet(root, id);
}
private Node doInoderGet(Node node, int id) {
Node temp = null;
// 如果有左结点,则先访问左结点
if (node.left != null) {
temp = doInoderGet(node.left, id);
}
// 如果temp!=null,则表示已经找到结点
if (temp != null) {
return temp;
}
// 左边结点没有找到,再判断当前结点是不是要找的结点
if (node.id == id) {
return node;
}
// 当前结点也不是要找的结点,那就找右结点
if (node.right != null) {
temp = doInoderGet(node.right, id);
}
// 无论最后右结点是否找到,都得返回
return temp;
}
2.3.6.3 后序查找
/**
* 根据id找结点,使用后序遍历
*
* @param id
* @return
*/
public Node postorderGet(int id) {
return doPostorderGet(root, id);
}
private Node doPostorderGet(Node node, int id) {
Node temp = null;
if (node.left != null) {
temp = doPostorderGet(node.left, id);
}
if (temp != null) {
return temp;
}
if (node.right != null) {
temp = doPostorderGet(node.right, id);
}
if (temp != null) {
return temp;
}
if (node.id == id) {
return node;
}
return temp;
}
3、顺序存储二叉树
3.1 概念
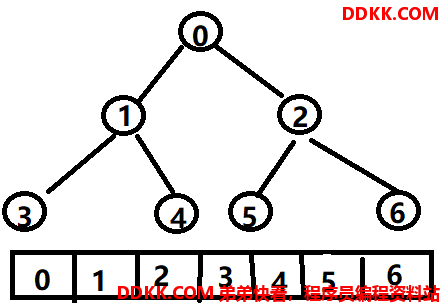
第二节二叉树的add方法是根据Node的id大小来放置到对应位置,使用的是链表结构。顺序存储二叉树是使用数组结构,原理是把二叉树从第一层开始,从左往右分别存储到数组的第0、1、2下标处。
3.2 代码实现
package cn.klb.datastructures.tree;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 顺序存储二叉树
* @Date: Create in 2023/4/12 21:15
* @Modified By:
*/
public class ArrBinaryTree {
private Node[] arr;
public ArrBinaryTree(Node[] arr) {
this.arr = arr;
}
/**
* 前序遍历
*/
public void preorderTraversal() {
if (arr.length == 0) {
System.out.println("数据为空,就不遍历了。");
return;
}
int index = 0;
doPreorderTraversal(index);
}
private void doPreorderTraversal(int index) {
// 打印当前结点
System.out.println(arr[index]);
// 向左递归
if (index * 2 + 1 < arr.length) {
doPreorderTraversal(index * 2 + 1);
}
// 向右递归
if (index * 2 + 2 < arr.length) {
doPreorderTraversal(index * 2 + 2);
}
}
/**
* 中序遍历
*/
public void inorderTraversal() {
if (arr.length == 0) {
System.out.println("数据为空,就不遍历了。");
return;
}
int index = 0;
doInorderTraversal(index);
}
private void doInorderTraversal(int index) {
// 向左递归
if (index * 2 + 1 < arr.length) {
doInorderTraversal(index * 2 + 1);
}
// 打印当前结点
System.out.println(arr[index]);
// 向右递归
if (index * 2 + 2 < arr.length) {
doInorderTraversal(index * 2 + 2);
}
}
/**
* 后序遍历
*/
public void postorderTraversal() {
if (arr.length == 0) {
System.out.println("数据为空,就不遍历了。");
return;
}
int index = 0;
doPostorderTraversal(index);
}
private void doPostorderTraversal(int index) {
// 向左递归
if (index * 2 + 1 < arr.length) {
doPostorderTraversal(index * 2 + 1);
}
// 向右递归
if (index * 2 + 2 < arr.length) {
doPostorderTraversal(index * 2 + 2);
}
// 打印当前结点
System.out.println(arr[index]);
}
}
3.3 测试代码
@Test
public void testGet(){
BinaryTree tree = new BinaryTree();
tree.add(new Node(8,"石鸣鸣"));
tree.add(new Node(6,"周杰伦"));
tree.add(new Node(4,"林俊杰"));
tree.add(new Node(2,"潘玮柏"));
tree.add(new Node(7,"赵本山"));
tree.add(new Node(5,"李云龙"));
tree.add(new Node(3,"赵日天"));
tree.add(new Node(1,"亮剑"));
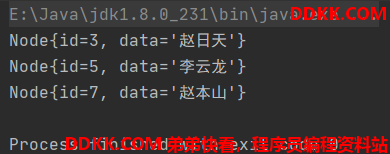
System.out.println(tree.preoderGet(3));
System.out.println(tree.inoderGet(5));
System.out.println(tree.postorderGet(7));
}
输出结果:
4、线索化二叉树
4.1 前提
一个二叉树结点有指向左子结点的指针和指向右子结点的指针,对于一个有n个结点的二叉树来说,总存在n+1个空指针,如下图所示:
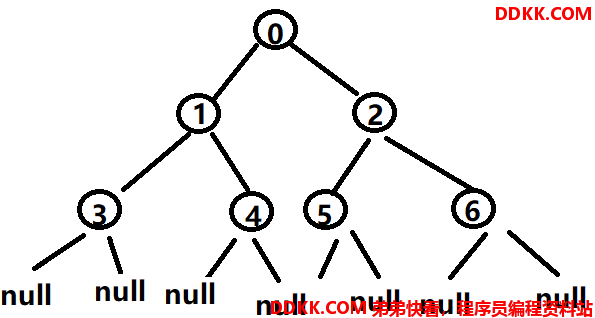
这里说明一下这个n+1是如何计算的。对于一个有n个结点的二叉树,每个结点都有左右子指针,所以总共有2n个指针。对于每一个结点,除了根结点,都有且仅有一条指向父节点的指针,所以非空指针有n-1个,所以空指针为2n-(n-1)=n+1。
对哪一个编程语言来说,空指针放在那里都是让人不舒服的。所以,有种方法叫做线索化二叉树,目的就是把空指针利用起来。
把原来空的指针指向二叉树的某个结点,这种指针称为线索,所以这个操作称为线索化。
4.2 线索化步骤
结点空指针指向哪一个结点是有规律的,而不是随便指向。一般是指向某个遍历顺序下该结点的下一个结点。
以中序遍历为例遍历二叉树:
1、若当前结点的左子结点为Null,则左子结点指向中序遍历中该结点的前驱结点;
2、若当前结点的右子结点为Null,则右子结点指向中序遍历中该结点的后继结点;
4.3 前驱结点和后继节点
这里先解释一下什么是前驱结点和后继结点。
假设存在一个二叉树如下所示:
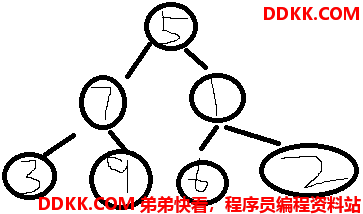
那么,中序遍历的结果为:{3,7,9,5,6,1,2}
很明显,结点3、9、6、2的左右结点都为Null。以结点9为例,根据中序遍历结果,9的左子结点指向结点7,这个结点7就叫做结点9的前驱结点,9的右子结点为结点5,这个结点5就叫做结点9的后继结点。
4.4 代码实现
package cn.klb.datastructures.tree;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 线索化二叉树
* @Date: Create in 2023/4/13 16:50
* @Modified By:
*/
public class ThreadedBinaryTree {
private ThreadNode root; // 二叉树根节点
private ThreadNode pre; // 线索化时,当前结点的前驱结点,初始时为null
/**
* 添加结点
*
* @param node
*/
public void add(ThreadNode node) {
if (root == null) {
root = node;
} else {
ThreadNode temp = root;
while (true) {
if (node.id < temp.id) {
if (temp.left != null) {
temp = temp.left;
} else {
temp.left = node;
break;
}
} else if (temp.id < node.id) {
if (temp.right != null) {
temp = temp.right;
} else {
temp.right = node;
break;
}
}
}
}
}
/**
* 线索化二叉树(中序遍历)
*/
public void threadedTree() {
threadNode(root);
}
/**
* 线索化结点
*
* @param node
*/
private void threadNode(ThreadNode node) {
// 空结点不线索化
if (node == null) {
return;
}
// 先线索化左子树
threadNode(node.left);
// 线索化当前结点
if (node.left == null) {
// 如果当前结点的左子结点为null
node.left = pre; // pre设置为前驱结点
node.leftType = true; // 设置为前驱结点标志
}
// 当前node的下一个结点是谁,目前不知道,等node成为了pre就知道了,到那时再设置后继结点
// 设置pre结点的后继结点(也就是上面注释未处理的后继节点)
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = true;
}
pre = node; // pre成为node,即准备遍历下一个
// 最后线索化右子树
threadNode(node.right);
}
/**
* 中序遍历
*/
public void inorderTraversal() {
doInorderTraversal(root);
}
/**
* 中序遍历递归执行
*
* @param node
*/
private void doInorderTraversal(ThreadNode node) {
// 向左递归
if (node.left != null && node.leftType == false) {
doInorderTraversal(node.left);
}
if (node.left != null && node.right != null) {
System.out.println("left:" + node.left + "---leftType:" + node.leftType + "---" + node + "---" + "right:" + node.right + "---rightType:" + node.rightType);
} else if (node.left == null) {
System.out.println("left:null" + "---leftType:false" + "---" + node + "---" + "right:" + node.right + "---rightType:" + node.rightType);
} else if (node.right == null) {
System.out.println("left:" + node.left + "---leftType:" + node.leftType + "---" + node + "---" + "right:null" + "---rightType:false");
}
// 向右递归
if (node.right != null && node.rightType == false) {
doInorderTraversal(node.right);
}
}
}
4.5 测试代码
@Test
public void testGet() {
BinaryTree tree = new BinaryTree();
tree.add(new Node(8, "石鸣鸣"));
tree.add(new Node(6, "周杰伦"));
tree.add(new Node(4, "林俊杰"));
tree.add(new Node(2, "潘玮柏"));
tree.add(new Node(7, "赵本山"));
tree.add(new Node(5, "李云龙"));
tree.add(new Node(3, "赵日天"));
tree.add(new Node(1, "亮剑"));
System.out.println(tree.preoderGet(3));
System.out.println(tree.inoderGet(5));
System.out.println(tree.postorderGet(7));
}
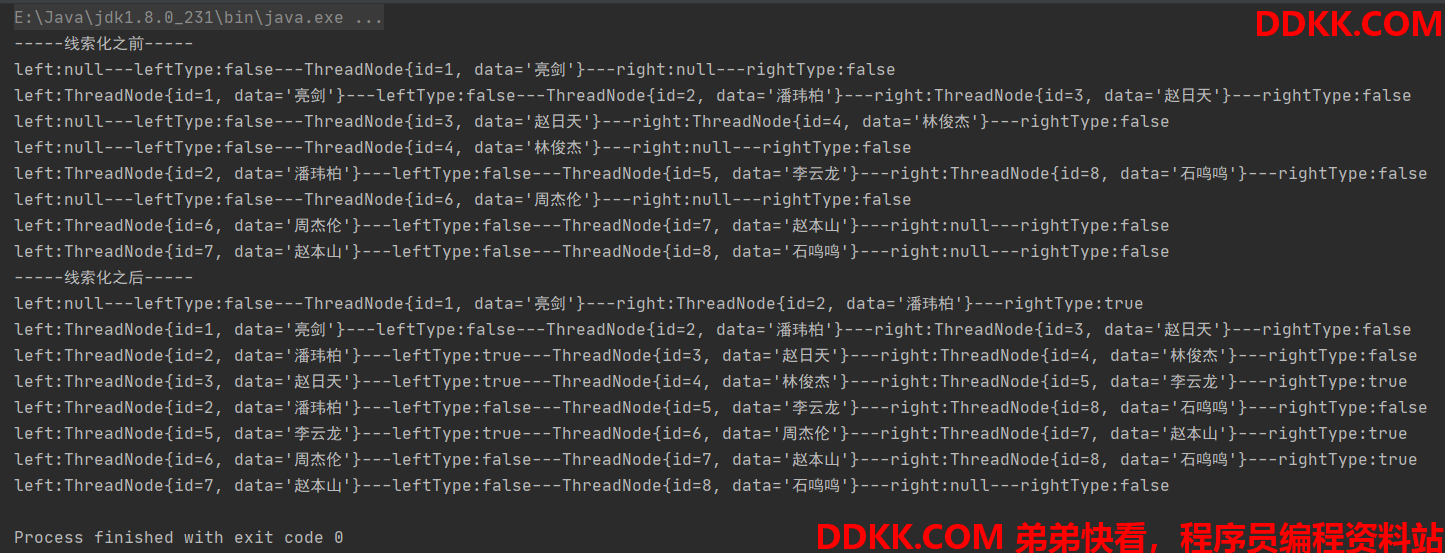
测试结果如下: