1、介绍
动态规划算法的核心思想是:把大问题划分为小问题进行解决,从而一步步获取最优解的处理算法。动态规划和分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。但是,与分治算法不同在于,适合用动态规划求解的问题,分解得到的子问题往往不是相互独立的(即下一个子问题的解是建立在上一个子问题的解的基础上进行进一步求解的)。
动态规划是可以通过填表的方式来逐步推进,得到最优解。
2、最佳实践:01背包问题
2.1 问题描述
有一个背包,承重为C,现在有重量分别为{w1,w2,…,wn}的n个物品(忽略体积),价值分别为{v1,v2,…,vn},问,在不超过背包承重且物品不重复的前提下,背包内物品的最大总价值。

2.2 递归思路
如果用函数f(i,j)表示将从前i个物品挑选物品放进容量为j的背包里,得到的最大的价值。假设我已经对前面n-1个物品已经挑选完毕,剩下最后一个物品,那么我们有两种选择:
1、不放入最后一个物品,此时总价值为 f(n-1,C);
2、放入最后一个物品,此时总价值为 vn + f(n-1,C-wn)。
然后两种选择当中的最大值就是我们的最终方案:
f(n,C) = max(f(n-1,C),vn + f(n-1,C-wn))
其实这就是子问题的拆解,子问题之间不是互相独立,而是依赖于前面的子结点。
递归到最前面就是从第一个物品中选择一个物品,,有两种选择:
1、不放入这个物品,此时总价值 f(0,C) = 0;
2、放入这个物品,此时总价值为 v1 + f(0,C-w1) = v1。
2.3 非递归思路
假设物品信息如下,背包承重为4磅。
| 物品 | 重量(磅) | 价格 |
|---|---|---|
| 吉他 | 1 | 1500 |
| 音响 | 4 | 3000 |
| 电脑 | 4 | 3000 |
遍历物品组合,下表为所有可能的最优解:
| 可选物品 | 0磅 | 1磅 | 2磅 | 3磅 | 4磅 |
|---|---|---|---|---|---|
| 空 | 0 | 0 | 0 | 0 | 0 |
| 吉他 | 0 | 吉他1500 | 吉他1500 | 吉他1500 | 吉他1500 |
| 吉他、音响 | 0 | 吉他1500 | 吉他1500 | 吉他1500 | 吉他1500 |
| 吉他、音响、电脑 | 0 | 吉他1500 | 吉他1500 | 电脑2000 | 吉他1500+电脑2000 |
定义一个二维数组value[][]来表示上表,其中value[i][j]表示容量为j时从前面i个物品中选择物品的组合的最大价值。
为什么需要这样的二维数组呢?是因为下面的计算要用到。
从顶层往下看,我现在准备放入第3个物品(电脑),这时我有两种选择:
1、不放,总价值为value[2][4];
2、放,总价值为v3 + value[2][4-w3]。
然后根据总价值:max{value[2][4],v3 + value[2][4-w3]}来决定放不放。
如果我是最后才看到电脑,在放前面两个物品之前我不知道电脑的存在,现在需要考虑放不放电脑了很明显就得根据三个物品的重量和价值来综合考虑,而这个“综合”就体现在value数组的第二个维度上,当w3=1或者=2或者=3,都会影响v3 + value[2][4-w3]的取值,所以放入每一个物品,都计算一遍书包承重变化所带来的决策变化,这样,当未来再新增物品时,能根据前面的计算结果马上得到最优解,而不是全部重新计算。
3、非递归代码实现
package cn.klb.algorithms.dynamic;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 动态规划的01背包问题
* @Date: Create in 2023/4/19 14:02
* @Modified By:
*/
public class Knapsack {
/**
* @param w 物品的重量数组,假设 w = {1,4,3},则表示有三个物品,重量分别为1 4 3
* @param v 物品的价值数组,假设 v = {1500,3000,2000},则表示这三个物品的价值分别是1500 3000 2000
* @param m 背包的承重,假设 m = 5,表示背包能放进的物品重量最大为5
* @return 背包承重为m的情况下,能装进的物品的最大总价值
*/
public static void calculate(int[] w, int[] v, int m) {
// 物品的个数
int n = w.length;
// 定义一个二维数组,大小为:(n+1)×(m+1)
// value[2][3] 表示当背包承重为3,物品只有前面两种的情况下能装进背包的物品最大总价值
// n+1和m+1 是为了计算包含了承重为0和物品数量为0的情况
// 初始状态每个值都为0
int[][] value = new int[n + 1][m + 1];
// 定义一个二维数组,大小为:(n+1)×(m+1)
// 用于跟踪value数组,当value数组每次更新更大的数值时进行记录
int[][] path = new int[n + 1][m + 1];
// 遍历所有组合
for (int i = 1; i < value.length; i++) {
// i == 1,表示当前只有1这一种物品
// i == 2,表示有1和2两种物品,即新添加了第i个物品,而不是只有第i个物品
// 以此类推
for (int j = 1; j < value[i].length; j++) {
// j == 1 表示背包承重为1
// j == 2 表示背包承重为2
// 以此类推
// 这里i-1是因为w和v索引都是从0开始有效
if (w[i - 1] > j) {
// 如果第i个物品的重量大于背包的承重j,就是只放第i个物品,也满足不了条件
// 那么,有i物品和j承重下的最大价值和没有i物品时j承重下的最大价值一样
value[i][j] = value[i - 1][j];
} else {
// 如果第i个物品的重量小于背包的承重
// 如果 w[i] <= j,那么计算两个值
// 1、oldData:value[i-1][j] 没有第i个物品时j承重下的最大价值
// 2、newData:v[i]+value[i-1][j-w[i]]:
// v[i]:表示第i个物品的价值
// j-w[i]:表示放进第i个物品后剩余的承重
// value[i-1][j-w[i]]:没有第i个物品,承重为j-w[i]时的最大价值
// 求 max 就是判断放进第i个物品后和没有放时哪个最大价值比较大
int oldData = value[i - 1][j];
int newData = v[i - 1] + value[i - 1][j - w[i - 1]];
value[i][j] = Math.max(oldData, newData);
if (oldData < newData) {
// 说明有更大的值更新了
path[i][j] = 1;
}
}
}
}
// 遍历输出所有可能的总价值
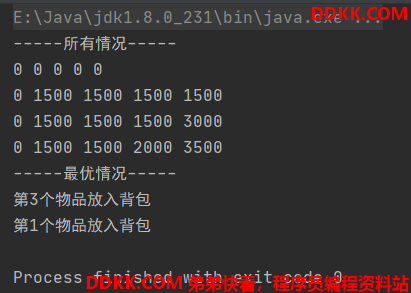
System.out.println("-----所有情况-----");
for (int i = 0; i < value.length; i++) {
for (int j = 0; j < value[i].length; j++) {
System.out.print(value[i][j] + " ");
}
System.out.println();
}
System.out.println("-----最优情况-----");
// 输出最大价值和对应的物品组合情况
int i = path.length - 1;
int j = path[0].length - 1;
while (i > 0 && j > 0) {
if (path[i][j] == 1) {
System.out.println("第" + i + "个物品放入背包");
j = j - w[i-1];
}
i--;
}
}
}
4、测试类
package cn.klb.test.algorithmstest;
import cn.klb.algorithms.dynamic.Knapsack;
import org.junit.Test;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description:
* @Date: Create in 2023/4/19 14:45
* @Modified By:
*/
public class KnapsackTest {
@Test
public void testKnapsack(){
int[] w = {
1,4,3};
int[] v = {
1500,3000,2000};
int m = 4;
Knapsack.calculate(w,v,m);
}
}
测试结果: