1、应用场景
Knuth-Morris-Pratt 字符串查找算法,简称为 KMP算法,常用于在一个文本串 S 内查找一个模式串 P 的出现位置。是用来代替暴力匹配算法的有效算法。

如果找到,即返回第一个字符的索引。
2、暴力匹配算法
2.1 案例展示
如果使用暴力匹配的思路如下:
首先设置两个指针i和j,分别指向S和P的首字符。
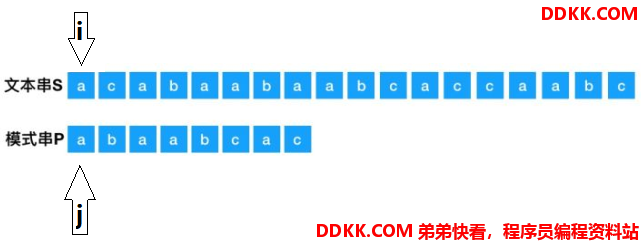
如果两个指针指向的字符相同,则两个指针同时往右移动一位,继续比较下一个字符,移动后如下:
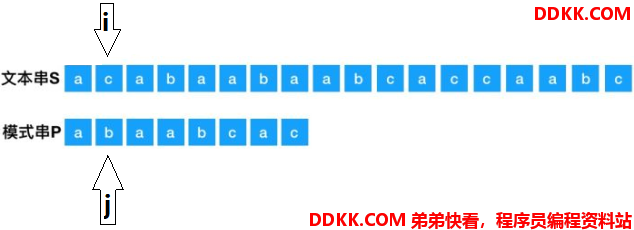
现在就已经匹配不上了,那么就要进行回溯操作,回溯操作即:i=i-j+1,j=0,即S的开始指针为上一次开始的起点的下一位,上一次的起点是S[0],那么这次的起点是S[1],P指针从0开始。回溯后如下:
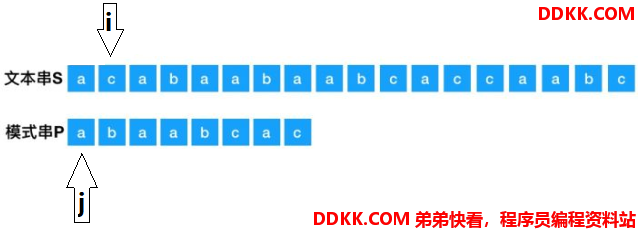
可以看出,第二轮直接第一个字符就不匹配了,就再进行回溯操作,i指针从上一次的起点的下一位开始,上一次的起点是S[1],现在的起点则是S[2]了,j从0开始,如下:
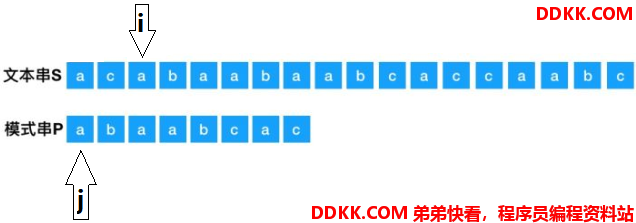
匹配的上,i和j同时往右走,这个例子中,两个指针往右走了5位,这时,两个指针指向的字符不一样了:
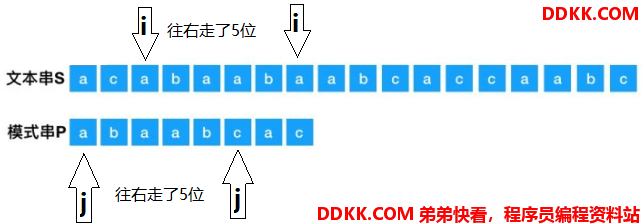
再次回溯,i回到上一次起点的下一位,上一次的起点是S[2],那么,现在的起点是S[3]了。j直接回到原点,回溯后如下:
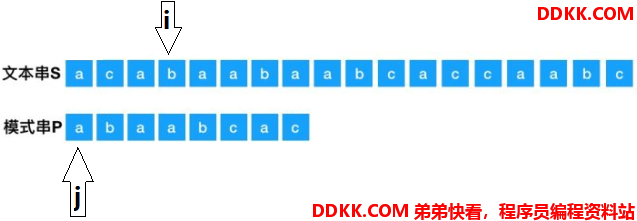
按照这种方法不断反复,直到第若干次回溯后,两个指针如下:
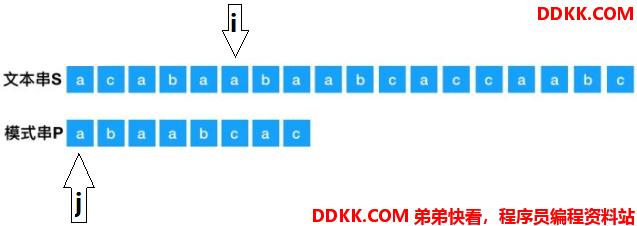
这时,两个指针继续匹配和往右移动,直到j移动的步数等于模式串P的长度减一,说明匹配到了:
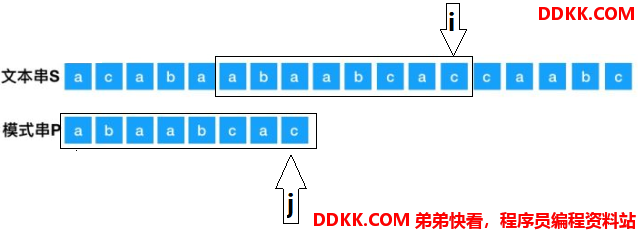
这时,就返回i-j,表示模式串P在文本串S第一次出现的首位置。比如现在i指向的是S[12],j指向的是P[7],那么P在S中第一次出现的首位置位12-7=5。
2.2 时间复杂度分析
假设文本串S的长度为m,模式串P的长度为n。最糟糕的情况就是每次都匹配到模式串P的最后一位才发现对不上。操作结束后,此时指针i回溯了m-n次,每次回溯完都要走n次才发现不匹配,当最后一轮时,走完n才发现匹配,此时共执行了(m-n)n+n=mn步,所以时间复杂度是O(mn)。
2.3 代码实现
package cn.klb.algorithms.kmp;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description:
* @Date: Create in 2023/4/20 23:43
* @Modified By:
*/
public class ViolenceMatch {
/**
* @param s 文本串
* @param p 模式串
* @return
*/
public static int match(String s, String p) {
// 模式串长度比文本串还长,肯定不是文本串的子串
if (s.length() < p.length()) {
return -1;
}
int i = 0; // 文本串s的指针
int j = 0; // 模式串p的指针
while (i < s.length() && j < p.length()) {
if (s.charAt(i) == p.charAt(j)) {
i++;
j++;
} else {
i = i - j + 1;
j = 0;
}
}
if (j == p.length()) {
return i - j;
} else {
return -1;
}
}
}
2.4 KMP算法对暴力匹配的改进
暴力匹配的缺点就在于回溯的方法,指针i每次都回到上一次起点的第二位。还是以这两个为例:

假设这时走到一下位置发现不匹配了:
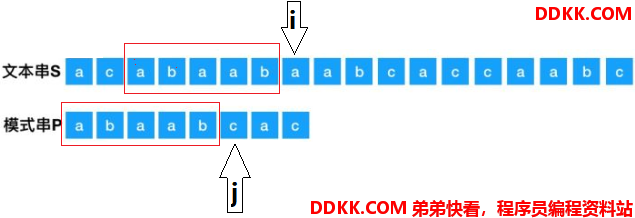
如果i又回溯到上一次起点的第二位,那么这一次模式串P扫描过的字符串“abaab”的信息就没有利用上了。
那么KPM就是在这里进行了改进,首先是指针i不动,指针j回到索引2的地方:
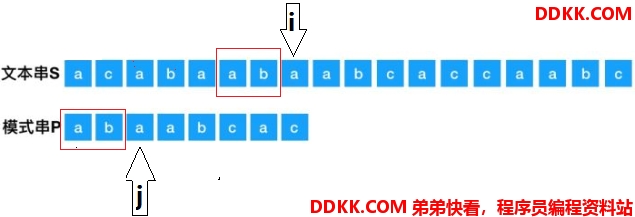
红色圈出来的地方是相同的,就等同于“ab”已经匹配过了,直接从P[2]位置开始了,极大的提高了匹配效率。
这时就引出了一个KMP算法的核心问题:这是什么原理?我怎么知道指针j移动到哪里?
3、 KMP算法
3.1 算法基本原理
假设匹配到以下位置发现不匹配:
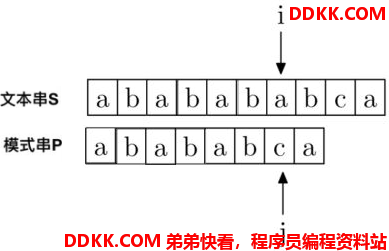
可以看出,模式串P从P[0]到P[j-1],都是匹配的,匹配的字符串为“ababab”。KMP算法会充分利用这个已匹配的信息,发现这个字符串的前四位和后四位居然是相同的。
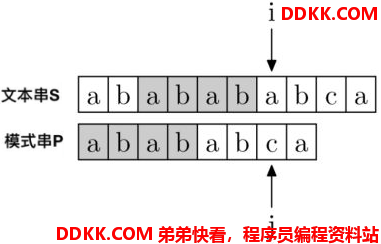
那么这四位就省略不用匹配了,i不用动,j直接去到模式串P的第4个位置P[4]开始:
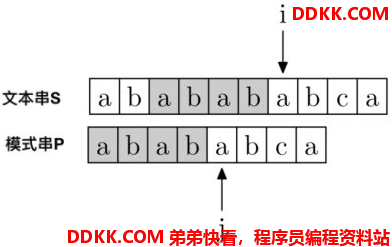
就等同于暴力匹配中第二次回溯,且匹配完了四个字符后的结果。KMP就是通过这种方式提高效率。
3.2 字符串的前缀和后缀
首先解释字符串的前缀和后缀,如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。要注意的是,字符串本身并不是自己的后缀。
而最大公共前后缀指的就是一个字符串中,前缀集合和后缀集合中,相同的字符串当中长度最大的那个。
比如字符串“ababab”,我们把它称之为“已匹配字符串”,顾名思义,就是当前已经匹配的上的字符串,从下一位开始才匹配不上。这个已匹配字符串的前缀集合为{"a","ab","aba","abab"},后缀集合为{"b","ab","bab","abab","babab"},相同字符串为{"ab","abab"},其中最长的为"abab",长度为4。这个4就是为什么上面的例子中,指针j直接回到第4个索引位置的原理了。
3.3 部分匹配表
看到上面这一节,仿佛觉得KMP算法不过如此嘛,这么简单。其实,上面只是说完了最简单的部分,最难的部分还是部分匹配表(Partial Match Table)的求解。
那什么是部分匹配表呢?首先还是回到上面那个例子,我把图再拷贝下来:
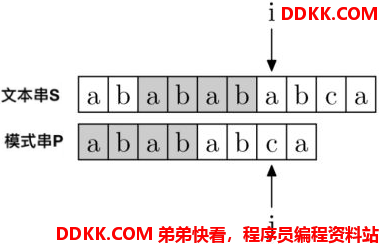
匹配到这里,先获取已匹配的字符串”ababab“,然后计算出这个字符串的前缀集合和后缀集合,最后找出公共前后缀字符串当中最长的那一个,长度为4,指针j就回到第4个位置。
难道每次不匹配,我都得重复这个过程来计算j应该回到第几个位置么,答案是否定的。我们在字符串匹配之前,就会建立一个叫做部分匹配表的一维数组。我们说的部分匹配表指的都是模式串P对应的部分匹配表。结果如下:
| 模式串P的字符 | a | b | a | b | a | b | c | a |
|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| value | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 |
这个表叫做部分匹配表,根据已匹配字符串计算出最大公共前后缀,比如,假如已匹配字符串为"aba",计算出前缀集合为{"a","ab"},然后计算出后缀集合为”ba“,"a",最大公共前后缀为”a“,长度为1,所以index为2的地方value为1,即每个index对应的value不是那个字符对应的value,而是字符串对应的。"a"对应0,"ab"对应0,"aba"对应1,"abab"对应2。以此类推。
上面例子的已匹配字符串为”ababab“,那就查看最后一个字符所对应的value,为4,那么指针j就回到第四位置开始。以此类推,如果已匹配字符串为”aba“,那么指针j就回到第1个位置;如果已匹配字符串为”ababa“,那么指针j就回到第3个位置。
这个表的使用方法就是:当遇到不匹配的地方时,根据已匹配字符串查找部分匹配表,就可以知道j回到哪个位置。
不过,虽然已匹配字符串对应的最大公共前后缀长度可以通过上面介绍的方法计算,但是对于程序来说过于繁杂,有大神已经总结出了一个计算流程,以字符串"abababca"为例,使用快捷方法计算部分匹配表:
定义一个一维数组prefix[]来存放,数组长度等于已匹配字符串的长度。
1、计算prefix[0],就是计算字符串"a"的最大公共前后缀长度,一眼即可看出,为0;
2、计算prefix[1],就是计算字符串"ab"的最大公共前后缀长度,定义两个指针,分别指向"abababca"字符串的首位和第1位:
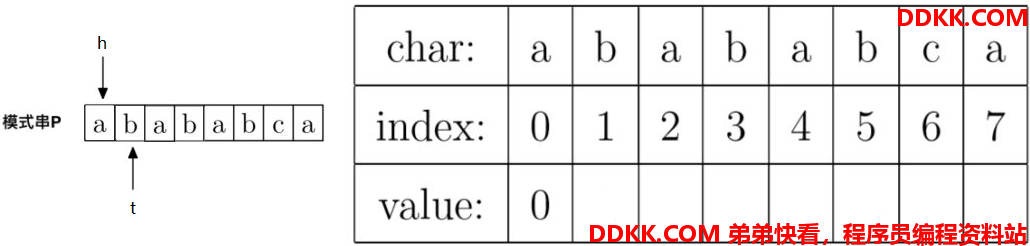
因为P[h] != P[t],即"a" != "b",且h == 0,所以prefix[t] = 0,即prefix[1] = 0。
此时指针t往右移动一位,指针h不动。移动后指针如下:
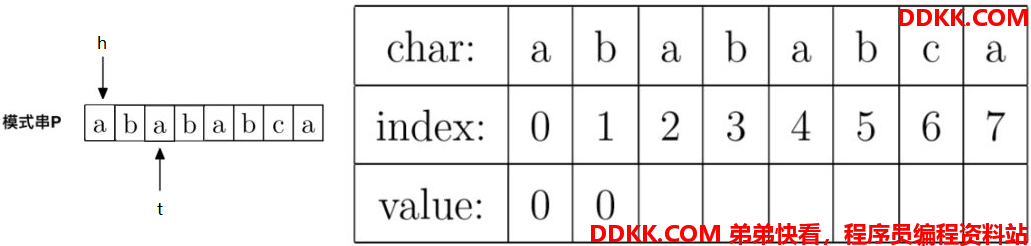
3、计算prefix[2],就是计算字符串“aba”的最大公共前后缀长度,因为P[h] == P[t],即"a" == "a",所以prefix[t] = h + 1,即prefix[2] = 0 + 1 = 1。
此时指针t往右移动一位,指针h往右移动一位。移动后指针如下:
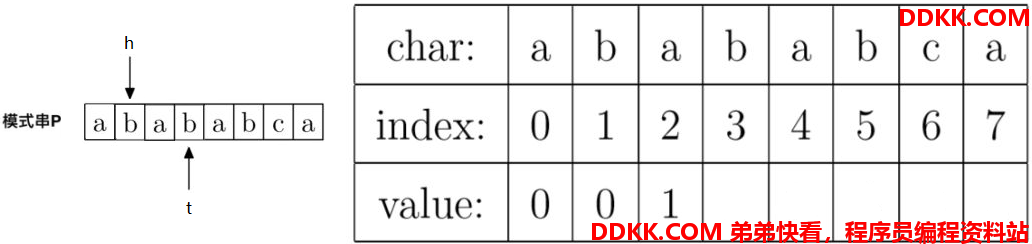
4、计算prefix[3],就是计算字符串"abab"的最大公共前后缀长度,因为P[h] == P[t],即"b" == "b",所以prefix[t] = h + 1,即prefix[3] = 1 + 1 = 2。
此时指针t往右移动一位,指针h往右移动一位。移动后指针如下:
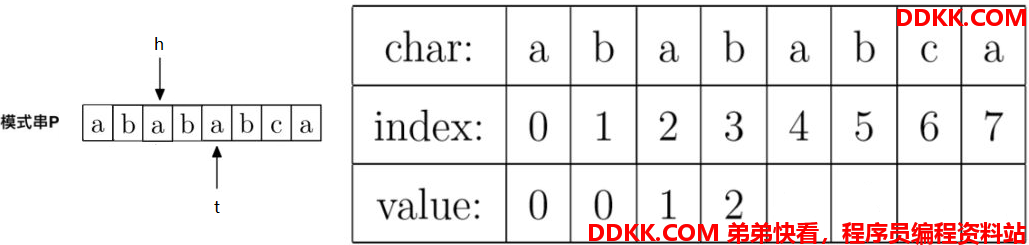
5、计算prefix[4],就是计算字符串"ababa"的最大公共前后缀长度,因为P[h] == P[t],即"a" == "a",所以prefix[t] = h + 1,即prefix[4] = 2 + 1 = 3。
此时指针t往右移动一位,指针h往右移动一位。移动后指针如下:
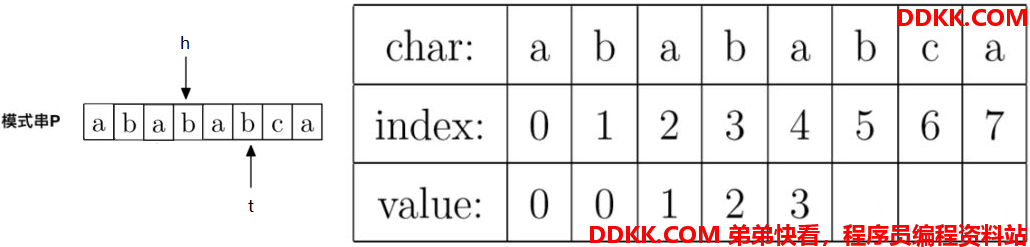
6、计算prefix[5],就是计算字符串"ababab"的最大公共前后缀长度,因为P[h] == P[t],即"b" == "b",所以prefix[t] = h + 1,即prefix[5] = 3 + 1 = 4。
此时指针t往右移动一位,指针h往右移动一位。移动后指针如下:
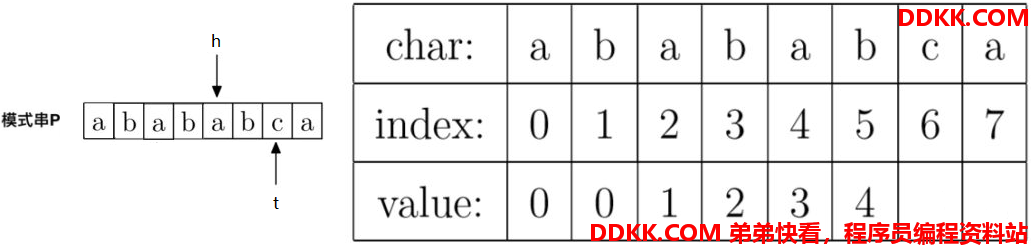
7、计算prefix[6],就是计算字符串"abababc"的最大公共前后缀长度,因为P[h] != P[t],即"a" != "c",所以先调整指针,t不动,h = prefix[h],即h调整到prefix[4] = 3的位置。调整后指针如下:
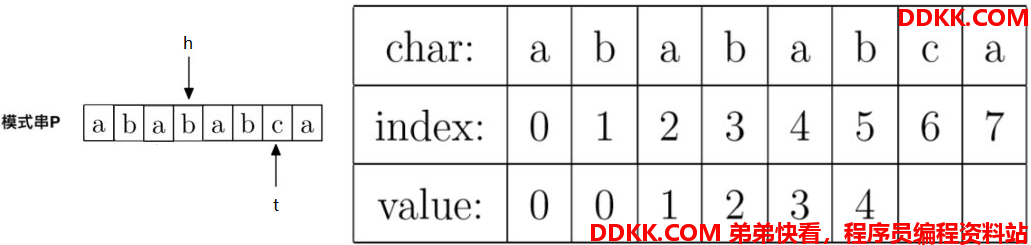
同理,还是P[h] != P[t],即"b" != "c",所以接着调整指针,t不动,h = prefix[h],即h调整到prefix[3] = 2的位置。调整后指针如下:
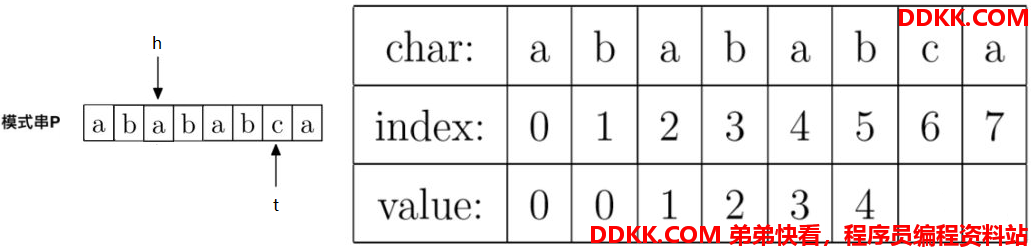
同理,还是P[h] != P[t],即"a" != "c",所以接着调整指针,t不动,h = prefix[h],即h调整到prefix[2] = 1的位置。调整后指针如下:
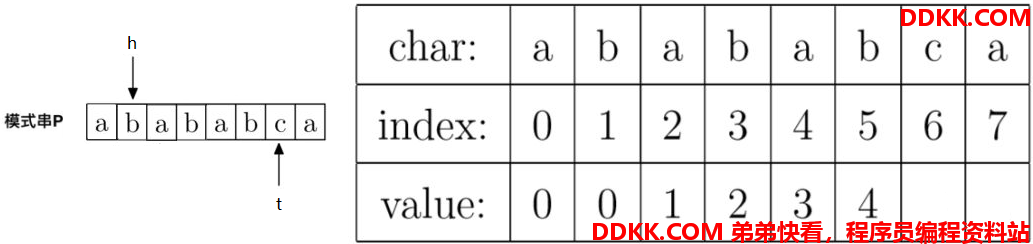
同理,还是P[h] != P[t],即"b" != "c",所以接着调整指针,t不动,h = prefix[h],即h调整到prefix[1] = 0的位置。调整后指针如下:
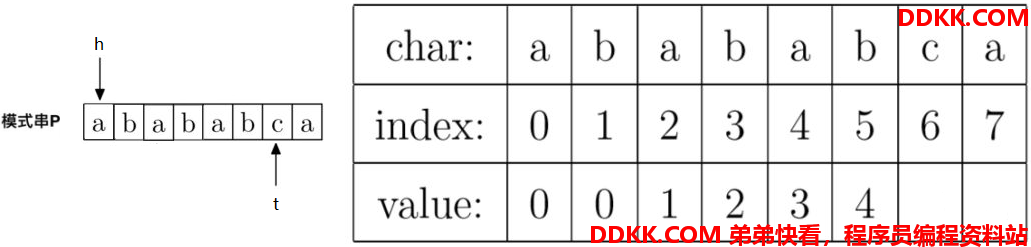
此时,还是P[h] != P[t],即"a" != "c",但是已经h == 0,因此,没得再调整了,直接prefix[6] = 0。此时,h不动,t往右走一位,调整后指针如下:
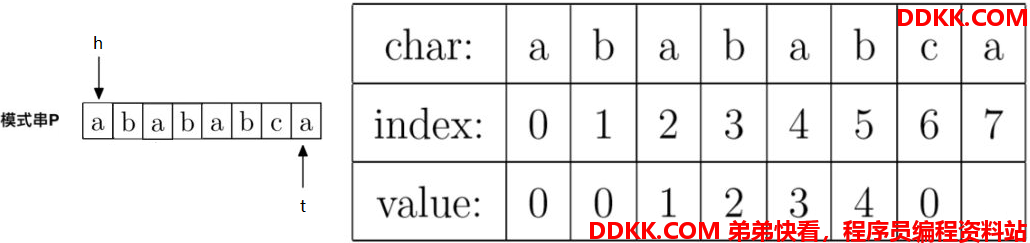
8、;计算prefix[7],就是计算字符串"abababc"的最大公共前后缀长度,因为P[h] == P[t],即"a" == "a",所以prefix[t] = h + 1,即prefix[7] = 0 + 1 = 1。
此时指针t往右移动一位,指针h往右移动一位。移动后指针如下:
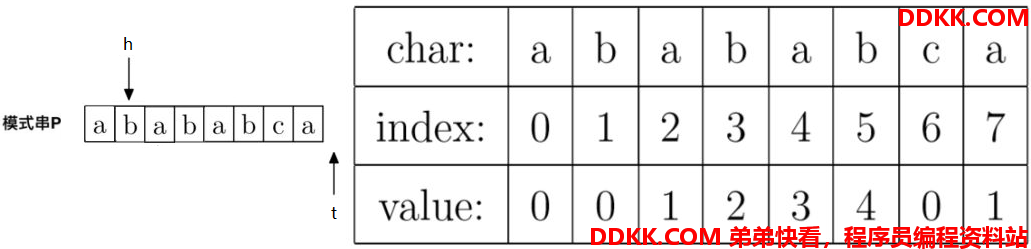
可以看出,此时指针t已经超出模式串P的最大长度,计算结束。
懵逼了吧,看到这个莫名其妙的计算过程,是不是在想:这个和前后缀有一毛钱关系?
开始介绍的前后缀计算过程是最直观,但是写起代码来就有点复杂了,而后面这个快速计算方法,计算过程最不直观,但是代码组织起来却很简单。这个快速计算方法计算得到的,和我们老老实实手算出来的是一模一样的,至于原理嘛,就得去看专门的论文了。这里我们只需要知道这样算的就行了。毕竟我们也不知道人工智能为什么能work,但是它就是work了。
有时候“知其所以然”对于我们的难度太高,而“知其然”却能够满足我们时候,那也可以接受吧。
下面来总结上面这个快速过程,以便我们组织代码。
1、指针h是有回到前面位置的,而指针t是只往前走的,t刚好是待计算字符串的尾指针;
2、我们计算prefix[t]的时候,是依赖于前面已经计算好的值(有点动态规划的味道了),所以不能跳跃计算;
3、其实计算过程就只有两个逻辑:
3.1、prefx[h] == prefix[t],那么就prefix[t] = h + 1;
3.2、prefx[h] != prefix[t],如果h != 0,则指针h回到prefix[h]的位置,然后重复步骤3。如果"h == 0",那么指针h就不用回溯了,直接prefix[t] = 0,然后h不动,t往下走一位,回到步骤3计算下一位。
根据我们总结好的这个1、2、3再回去看快速计算的图解过程,就不会那么莫名其妙了。
3.4 next数组
上面计算好了prefix[],如果在i处开始不匹配,那么0到i-1就是已匹配字符串,根据prefix[i-1]来计算出指针j要回到哪里。
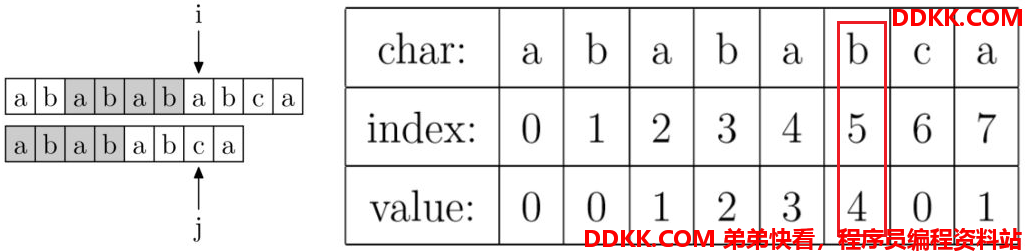
然后很多教材为了编程的美观,就把这个prefix[]数组整体往右移动一位,变成如下:
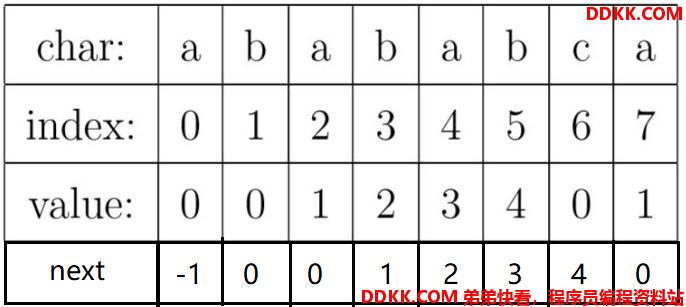
有同学会说:不对啊,这样子最后一位value不就丢失了么?
其实最后一位是没啥用的,因为如果已匹配字符串就是模式串P,那你不就已经匹配成功了么,还要部分匹配表干啥?
有了next[],就可以直接next[i]了,而不用prefic[i-1], 多直观啊!(无奈的语气)
然后这个next[0] = -1其实是没啥意义的,就是编程的时候用来做判断用的。
3.5 代码实现
package cn.klb.algorithms.kmp;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: KMP算法实现字符串比较
* @Date: Create in 2023/4/20 14:18
* @Modified By:
*/
public class KMP {
/**
* 给定一个主串s及一个模式串p,判断模式串是否为主串的子串;若是,返回匹配的第一个元素的位置(序号从0开始),否则返回-1
*
* @param s 源字符串
* @param p 需要匹配的字符串
* @return s首次出现p的索引
*/
public static int match(String s, String p) {
// 长度比主串还长,肯定不是主串的子串
if (s.length() < p.length()) {
return -1;
}
int[] next = getNext(p); // 获取模式串对应的next数组
int i = 0;
int j = 0;
while (i < s.length() && j < p.length()) {
if (j == -1 || s.charAt(i) == p.charAt(j)) {
i++;
j++;
} else {
j = next[j];
}
}
if (j == p.length()) {
return i - j;
} else {
return -1;
}
}
/**
* 根据字符串获取next数组
*
* @param str
* @return
*/
public static int[] getNext(String str) {
int[] next = getPrefix(str);
for (int i = next.length - 1; i >= 0; i--) {
if (i == 0) {
next[0] = -1;
} else {
next[i] = next[i - 1];
}
}
return next;
}
/**
* 获取字符串对应的prefix数组
*
* @param str
* @return
*/
public static int[] getPrefix(String str) {
int[] prefix = new int[str.length()];
prefix[0] = 0;
int t = 1;
int h = 0;
while (t < str.length()) {
if (str.charAt(t) == str.charAt(h)) {
prefix[t] = h + 1;
t++;
h++;
} else {
if (h == 0) {
prefix[t] = 0;
t++;
} else {
h = prefix[h - 1];
}
}
}
return prefix;
}
}
3.6 测试代码
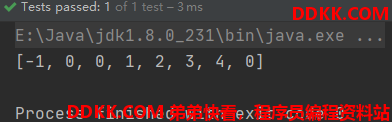
测试一下,假设已匹配字符串为"abababca"时,我们手算的next数组是否和代码计算结果一致。
测试代码如下:
@Test
public void testGetNext(){
String str = "abababca";
System.out.println(Arrays.toString(KMP.getNext(str)));
}
输出如下:
再测试一下KMP的比较结果,测试代码如下:
@Test
public void testKMP(){
String str1 = "AAAAABCDABDRRRR";
String str2 = "ABCDABD";
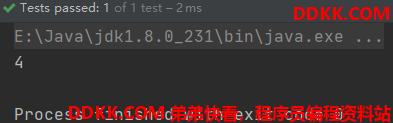
System.out.println(KMP.match(str1,str2));
}
运行结果如下:
3.7 时间复杂度
假设文本串S的长度为m,模式串长度为n。计算next数组时候花费的步骤为n,然后匹配时候花费步骤为m。时间复杂度为O(m+n),比暴力匹配的O(mn)好很多。