1、线性查找
1.1 原理
线性查找是最简单的查找方法,直接就是比较每一个元素,优点是对带搜索数列没有什么要求。
1.2 代码实现
package cn.klb.datastructures.search;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 对数组序列的线性查找
* @Date: Create in 2023/4/9 13:27
* @Modified By:
*/
public class Linear {
public static int search(int[] arr, int key) {
int index = -1;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == key) {
index = i;
}
}
return index;
}
}
2、二分查找
2.1 原理
二分查找的前提是待搜索数组必须是有序的。
设待查寻的值为value,待搜索数组最左端索引位left,最右端索引位right。则正中间的所有mid=(left+right)/2。
比较 value和arr[mid]值大小,小于,则right更新为mid-1;反之left更新为mid+1;重复上面操作,直到找到索引。若left>right,说明找不到,返回-1。
2.2 代码实现
package cn.klb.datastructures.search;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 实现从小到大有序数组的二分查找
* @Date: Create in 2023/4/9 13:36
* @Modified By:
*/
public class Binary {
public static int search(int[] arr, int key) {
int index = -1; // 要返回的key在arr中的索引
// 如果待查寻的值比最小值还小或比最大值还大,直接返回-1
if (key < arr[0] || arr[arr.length - 1] < key) {
return index;
}
int left = 0; // 初始左索引
int right = arr.length - 1; // 初始右索引
int mid = 0;
while (left <= right) {
mid = midOf(left,right); // 更新中间索引
if (arr[mid] < key) {
// 待检索的值比中间值还大
left = mid + 1; // left更新为arr右半部分的开头
} else if (key < arr[mid]) {
// 带检索的值比中间值还小
right = mid - 1; // right更新为arr左半部分的末尾
} else {
index = mid; // key和arr[mid]相等,索引赋值
break; // 找到index即跳出循环
}
}
return index;
}
// 二分查找的中间索引计算方法
private static int midOf(int left,int right){
return (left + right + 1) / 2;
}
}
3、插值查找
3.1 原理
插值查找算法和二分查找算法类似,不同之处在于:插值查找的mid不是取中间索引,而是自适应生成。
和二分查找算法的mid计算区别如下:

3.2 代码实现
package cn.klb.datastructures.search;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 实现从小到大有序数组的插值查找
* @Date: Create in 2023/4/9 14:11
* @Modified By:
*/
public class Interpolation {
public static int search(int[] arr, int key) {
int index = -1;
// 如果待查寻的值比最小值还小或比最大值还大,直接返回-1
if (key < arr[0] || arr[arr.length - 1] < key) {
return index;
}
int left = 0;
int right = arr.length - 1;
int mid = 0; // 插值查找的中间索引
while (left < right) {
mid = midOf(arr, left, right, key); // 更新中间索引
if (arr[mid] < key) {
// 待检索的值比中间值还大
left = mid + 1; // left更新为arr右半部分的开头
} else if (key < arr[mid]) {
// 带检索的值比中间值还小
right = mid - 1; // right更新为arr左半部分的末尾
} else {
index = mid; // key和arr[mid]相等,索引赋值
break; // 找到index即跳出循环
}
}
return index;
}
// 插值查找的中间索引计算方法
private static int midOf(int[] arr, int left, int right, int key) {
return left + ((key - arr[left]) / (arr[right] - arr[left])) * (right - left);
}
}
4、斐波那契查找
斐波那契查找算法和二分查找也是类似,不同点也是在于mid的取值策略。
4.1 斐波那契数列
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、····,在数学上,斐波那契被递归方法如下定义:F(1)=1,F(2)=1,F(n)=f(n-1)+F(n-2) (n>=2)。该数列越往后相邻的两个数的比值越趋向于黄金比例值(0.618)。
4.2 mid取值策略
假设待搜索的数组 arr = {1,3,5,7,9,11,13,15,17},arr长度为9。对应斐波那契数列中的F[6]=13,给arr数组长度补充到13,补充方法就是复制最后一个值。新的 arr1 = {1,3,5,7,9,11,13,15,17,17,17,17,17}。然后arr1可以看成F[5]个前数组和F[4]个后数组组成的。而mid即为这个黄金分割点附近对应的元素。
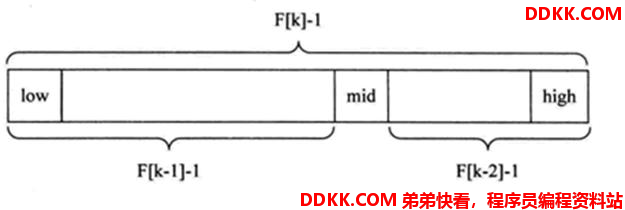
减一是因为数组的索引是从0开始,F[6] - 1 = 13 - 1 = 12,即:low为0,high为12。
对于arr1长度为F[6]=13,因此mid = low + F[6-1] - 1 = 0 + 8 - 1 = 7。
如果 value < arr1[mid],即value < arr1[7],则value在前面一截数组中,然后mid更新为前面这截数组的黄金分割点。
4.3 代码实现
package cn.klb.datastructures.search;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 实现从小到大有序数组的斐波那契查找
* @Date: Create in 2023/4/8 22:52
* @Modified By:
*/
public class Fibonacci {
public static int search(int[] arr, int key) {
int index = -1;
// 如果待查寻的值比最小值还小或比最大值还大,直接返回-1
if (key < arr[0] || arr[arr.length - 1] < key) {
return index;
}
int low = 0; // 待搜索数组最左端
int high = arr.length - 1; // 待搜索数组最右端
List<Integer> f = fib(arr.length); // 斐波那契数组
int k = f.size() - 1; // k为待搜索数组长度所对应的斐波那契数组的数的下标
int[] arr1 = Arrays.copyOf(arr, f.get(k)); // 新建一个数组,长度为斐波那契数组第k个索引对应的数
// 如果初始待搜索数组长度不是对应斐波那契数组某个数,那就填充到对应上
for (int i = arr.length; i < k; i++) {
arr1[i] = arr[arr.length - 1];
}
int mid = 0;
while (low <= high) {
mid = midOf(low, f.get(k - 1)); // 斐波那契查找法计算出的中间值
if (key < arr1[mid]) {
k = k - 1;
high = mid - 1;
} else if (arr1[mid] < key) {
k = k - 2;
low = mid + 1;
} else {
// arr1是从arr拷贝过来的,后面是重复值,所以要确定返回哪一个下标
if (mid <= high) {
index = mid;
} else {
index = high;
}
break;
}
}
return index;
}
// 斐波那契查找的中间索引计算方法
private static int midOf(int low, int f) {
return low + f - 1;
}
// 生成斐波那契数组
private static List<Integer> fib(int arrLength) {
List<Integer> f = new ArrayList<Integer>();
f.add(0, 1);
for (int i = 1; f.get(f.size() - 1) < arrLength; i++) {
if (i == 1) {
f.add(i, 1);
} else {
f.add(i, f.get(i - 1) + f.get(i - 2));
}
}
return f;
}
}