1、二叉排序树(二叉搜索树、二叉查找树)
1.1 介绍
二叉排序树(又叫二叉搜索树、二叉查找树)是二叉树的一种,它是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
特别说明:如果有相同的值,可以放在左子结点或右子结点。
比如针对数据{7,3,10,12,5,1,9},对应二叉排序树为:
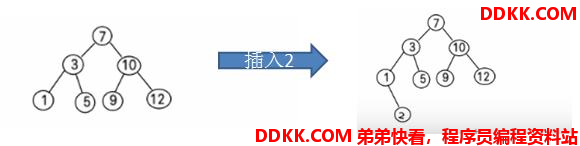
1.2 二叉排序树的删除
1.2.1 可能的情况
二叉排序树的删除需要考虑三种情况:
1、删除叶子结点(比如:2、5、9、12)
2、删除只有一棵子树的结点(比如:1)
3、删除有两棵子树的结点(比如:7、3、10)
对于情况一:假设要删除的是图中的结点5,只需要把它的父结点3的右结点设置为null即可;
对于情况二:假设删除的是图示的结点1,只需要把结点1的子结点2设置为结点3的左结点即可;
对于情况三:假设要删除的是结点7,先找出结点7的右子树的最小值结点,比如图示里为9,然后结点9赋值给结点7,删除结点9即可。
1.2.1 代码解决流程
情况一:
1、找到要删除的结点targetNode和它的父结点parentNode;
2、如果targetNode是parentNode的左结点,则parentNode.left=null;如果targetNode是parentNode的右结点,则parentNode.right=null。
情况二:
1、找到要删除的结点targetNode和它的父结点parentNode;
2、如果targetNode是parentNode的左子结点,则把parentNode.left=targetNode.left(或targetNode.right),如果targetNode是parentNode的右子结点,则把parentNode.right=targetNode.left(或targetNode.right)。
情况三:
1、找到要删除的结点targetNode和它的父结点parentNode(如果是根结点就不需要找parentNode);
2、用一个临时变量把targetNode右子树的最小值的结点的value保存起来,比如:int temp = minNode.value;
3、执行:targetNode.temp = 11;
4、然后把minNode删除了。(minNode一定是叶子结点,删除参考情况一)
1.3 删除的代码实现
/**
* 删除指定value的结点
* @param value
*/
public void remove(int value) {
// 先查看这个要删除的结点是否存在
Node targetNode = search(value);
if (targetNode == null) {
System.out.println("要删除的结点不存在!");
return;
}
// 如果要删除的是根结点,就不需要找父结点了
if (root.value == value) {
if (root.right == null) {
root = root.left;
} else {
// 先找到这个结点的右子树中value最小的结点
Node min = findMinValueNode(root.right);
// 用临时变量把这个最小值保存起来,如:int temp = 11
int temp = min.value;
// 删除该最小结点
remove(min.value);
root.value = temp;
}
} else {
// 如果要删除的不是根结点,就需要找父结点
Node parentNode = searchParent(value);
// 判断三种情况
if (targetNode.left == null && targetNode.right == null) {
// 情况一:删除叶子结点
if (parentNode.right == targetNode) {
parentNode.right = null;
} else {
parentNode.left = null;
}
} else if (targetNode.left != null && targetNode.right != null) {
// 情况三:删除有两颗子树的结点
// 先找到这个结点的右子树中value最小的结点
Node min = findMinValueNode(targetNode.right);
// 用临时变量把这个最小值保存起来,如:int temp = 11
int temp = min.value;
// 删除该最小结点
remove(min.value);
targetNode.value = temp;
} else {
// 情况二:删除只有一棵子树的结点
if (parentNode.left == targetNode) {
if (targetNode.left != null) {
parentNode.left = targetNode.left;
} else {
parentNode.left = targetNode.right;
}
} else if (parentNode.right == targetNode) {
if (targetNode.left != null) {
parentNode.right = targetNode.left;
} else {
parentNode.right = targetNode.right;
}
}
}
}
}
/**
* 找出结点的右子树中的最小值的结点
*
* @return
*/
private Node findMinValueNode(Node node) {
while (true) {
if (node.left != null) {
node = node.left;
} else {
return node;
}
}
}
/**
* 找到值为 value 的结点的父结点,找到则返回,找不到则返回null,如果值为 value 的结点是根结点,则返回null
*
* @param value
* @return
*/
private Node searchParent(int value) {
Node parentNode = root;
Node targetNode;
if (parentNode.value < value) {
targetNode = parentNode.right;
while (true) {
if (targetNode.value < value) {
parentNode = targetNode;
targetNode = parentNode.right;
} else if (targetNode.value > value) {
parentNode = targetNode;
targetNode = parentNode.left;
} else {
return parentNode;
}
}
} else {
targetNode = parentNode.left;
while (true) {
if (targetNode.value < value) {
parentNode = targetNode;
targetNode = parentNode.right;
} else if (targetNode.value > value) {
parentNode = targetNode;
targetNode = parentNode.left;
} else {
return parentNode;
}
}
}
}
/**
* 根据 value 查找结点,找到就返回该结点,否则返回null
*
* @param value
* @return
*/
public Node search(int value) {
Node temp = root;
while (true) {
if (temp != null) {
if (temp.value < value) {
temp = temp.right;
} else if (temp.value > value) {
temp = temp.left;
} else {
return temp;
}
} else {
return null;
}
}
}
2、平衡二叉树
2.1 问题的提出
如果有一个数列{1,2,3,4,5},要求创建一棵二叉排序树,创建结果如下:
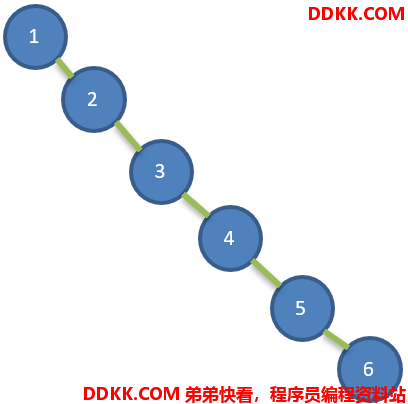
可以看出存在以下问题:
1、左子树全部为空,形式上更像一个单链表;
2、插入速度没影响,但查询速度明显降低(要判断左子树是否存在),查询速度比单链表还慢;
解决这些问题的方案是平衡二叉树(AVL)
2.2 介绍
平衡二叉树的特点:它是一棵空树或它的左右两颗子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
下面举个例子:
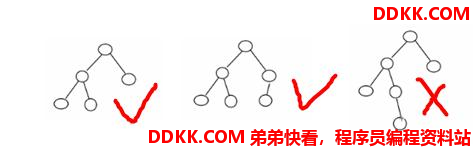
把一颗不平衡的二叉树变为平衡的方法是左旋或右旋。
2.3 左旋

左旋是先进行逆时针旋转,使得根结点(结点4)的右结点(结点6)放到根结点的位置,然后调整结点4和结点6的左右指针:原根结点(结点4)的右结点指针指向新根结点(结点6)之前的左结点(结点5),新根结点(结点6)的的左结点指针指向原来的根结点(结点4)。
2.4 右旋
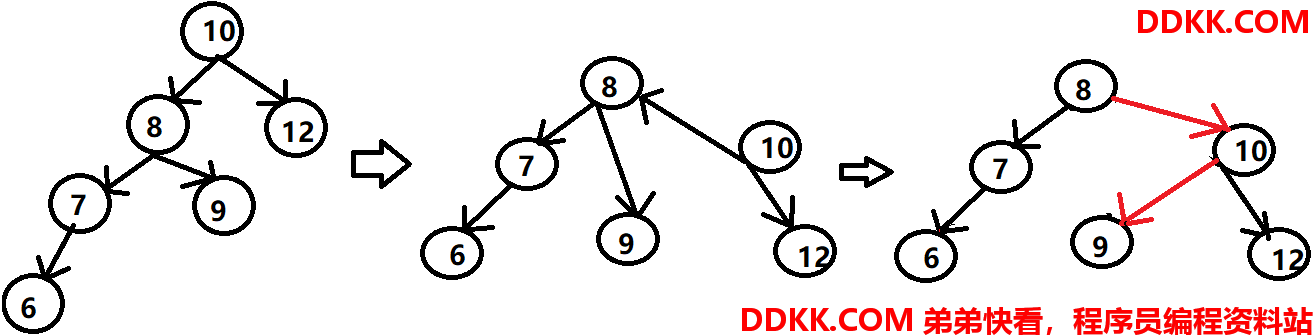
右旋就是先进行顺时针旋转,使得根结点(结点10)的左结点(结点8)放到根结点的位置,然后调整结点10和结点8的左右结点指针:原根结点(结点10)的左结点指针指向新根结点(结点8)之前的右结点(结点9),新根结点(结点8)的右结点指针指向原来的根结点(结点10)。
2.5 代码实现
2.5.1 左旋和右旋的代码逻辑
对于一个根结点来说,会有一个Node类型的变量root指向它,因此,在左旋和右旋的时候,不能改变root指向的内容。比如下图的左旋示意图:

开始的时候,root变量指向结点4,当左旋结束后,root应该指向结点6,而不是结点4。
因此,代码实现左旋右旋的逻辑会略微繁琐。
左旋逻辑:
1、创建一个新结点newNode,value和root结点的value一样;
2、newNode的左结点设置为root结点的左结点(结点3):newNode.left=root.left;
3、newNode的右结点设置为根结点的右结点的左结点(结点5):newNode.right=root.right.left;
4、把root结点的value更新为root结点的右结点(结点6)的value:root.value=root.right.value;
5、把root结点的左结点设置为newNode:root.left=newNode;
图解如下:
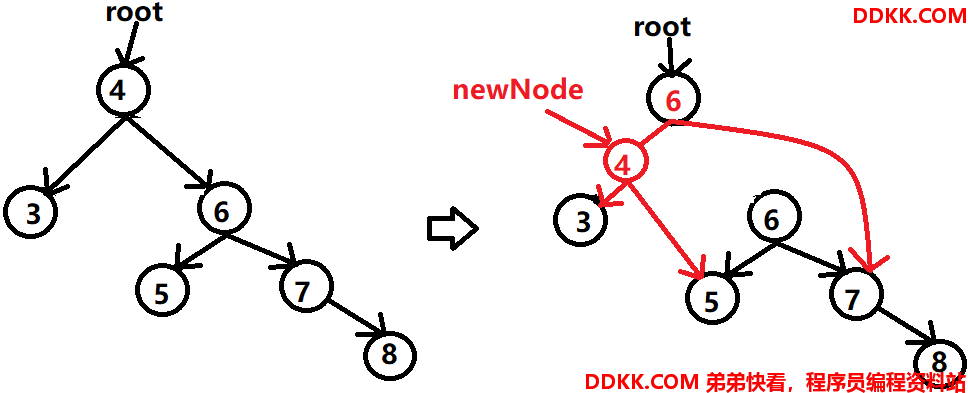
原来的结点6因为没有引用,会被JVM当成垃圾清理掉。
右旋也是一样的道理。
2.5.2 左旋代码
/**
* 对以结点node为根结点的二叉树进行左旋
* 操作流程是:根结点变为右结点的左结点,右结点变为新的根结点,新的根结点的左结点为旧的根结点
* 至于代码为什么这么复杂,是为了顾及变量的引用问题,比如 root指向一个结点A,左旋后 root应该指向新的根结点B,而不是原来那个结点A
*
* @param node
*/
public void leftRotate(Node node) {
// 创建新的结点,value和根结点的value相同
Node newNode = new Node(node.value);
// 新结点的右结点为根结点的右结点的左结点
newNode.right = node.right.left;
// 新结点的左结点为根结点的左结点
newNode.left = node.left;
// 根结点的值更新为根结点右结点的值
node.value = node.right.value;
// 根结点的左结点更新为新结点
node.left = newNode;
// 根结点的右结点更新为右结点的右结点
node.right = node.right.right;
}
2.5.3 右旋代码
/**
* 对以结点node为根结点的二叉树进行右旋
*
* @param node
*/
public void rightRotate(Node node) {
// 创建新的结点,value和根结点的value相同
Node newNode = new Node(node.value);
// 新结点的右结点为根结点的右结点
newNode.right = node.right;
// 新结点的左结点为根结点的左结点的右结点
newNode.left = node.left.right;
// 根结点的值更新为根结点左结点的值
node.value = node.left.value;
// 根结点的右结点更新为新结点
node.right = newNode;
// 根结点的左结点更新为左结点的左结点
node.left = node.left.left;
}
2.6 双旋转的情况
当存在下面这样的二叉树:
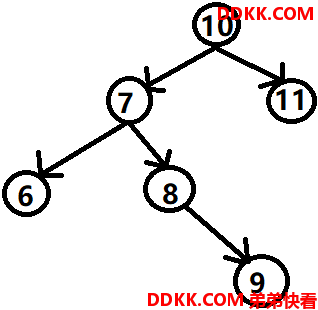
根结点的左子树高度为3,右子树高度为1,不符合平衡二叉树特性,所以需要右旋,右旋后的结果如下:
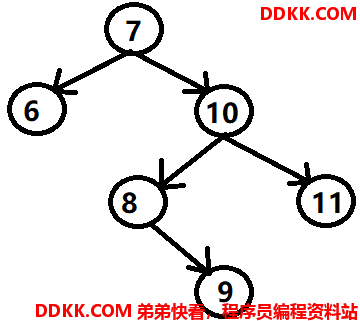
旋转后,根结点的右子树高度为3,左子树高度为1,不符合平衡二叉树特性,所以需要左旋。。。(禁止套娃!)
这里的问题出在:初始时(根结点为10),左子树高度大于右子树。来分析左子树,左子树的根结点为结点7,结点7为根结点的树的高度为3主要是结点7的右结点影响的,以结点10为根结点进行右旋后,这个结点7的右子树就全部作为结点10的左子树,导致右旋后以结点7为根结点的树还是不平衡。
因此,判断是否右旋,不仅先判断左子树的高度是否比右子树的高度高出1,还得对左子树进行判断,判断左子树是否右重左轻,如果是,则先对这课左子树进行左旋,然后再整体右旋。
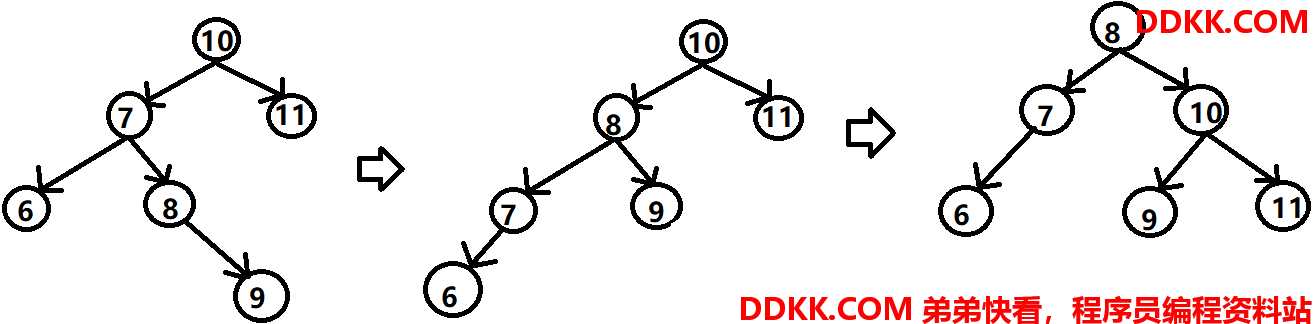
代码如下:
/**
* 获取二叉树的高度
*
* @param node 二叉树的根结点
* @return
*/
public int getHeight(Node node) {
if (node == null) {
return 0;
} else {
int leftHeight; // 左结点的高度
int rightHeight; // 右结点的高度
if (node.left != null) {
leftHeight = getHeight(node.left);
} else {
leftHeight = 0;
}
if (node.right != null) {
rightHeight = getHeight(node.right);
} else {
rightHeight = 0;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
public void add(Node node) {
doAdd(node);
// 添加完后判断是否平衡
if ((getHeight(root.left) - getHeight(root.right)) > 1) {
// 如果左子树较高,则进行右旋
// 右旋之前先判断root的左子树的右子树高度是否大于root的左子树的左子树高度
if (getHeight(root.left.right) > getHeight(root.left.left)) {
// 对左子树先进行一次左旋
leftRotate(root.left);
}
rightRotate(root);
} else if ((getHeight(root.right) - getHeight(root.left)) > 1) {
// 如果右子树较高,则进行左旋
// 左旋之前先判断root的右子树的左子树高度是否大于root的右子树的右子树高度
if (getHeight(root.right.left) > getHeight(root.right.right)) {
// 对右子树先进行一次右旋
rightRotate(root.right);
}
leftRotate(root);
}
}