1、基本思想
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。一个待排序的数组,把它看成是顺序存储的二叉树,假设要升序排列,先把这个二叉树调整为大顶堆,其顶端元素为最大值,把顶端元素和末尾元素互换后,再次把堆调整为大顶堆。如此循环,直到整个数组排序完毕。
2、图解
2.1 大顶堆和小顶堆
堆是完全二叉树,堆分为大顶堆和小顶堆。
每个结点的值都大于或等于其左右子结点的值,称为大顶堆;反之称为小顶堆。
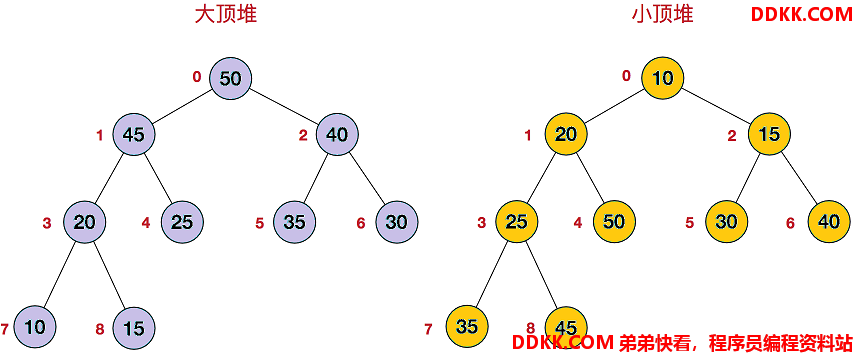
用前面学到的顺序存储二叉树,讲这种逻辑结构映射到数组中就变成了:

从数组上讲,在没有超出索引情况下用公式来描述堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
2.2 二叉树调整为大顶堆
一个二叉树调整为堆结构的大前提是这个二叉树是完全二叉树。
以调整为大顶堆为例。
假设存在一个二叉树如下所示:
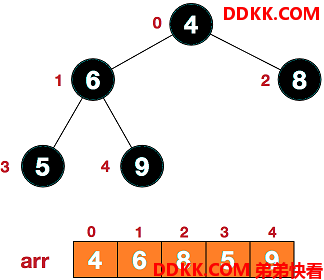
第一步:从最后一个非叶子结点开始调整(最后一个非叶子节点的索引为arr.length/2-1),此处是 5/2-1=1,也就是值为6的结点。先找出该结点的左右子结点中值最大的子结点,这里是第4个结点,值为9。然后判断该子结点是否大于该结点,9 > 6,于是交换结点6和结点9。
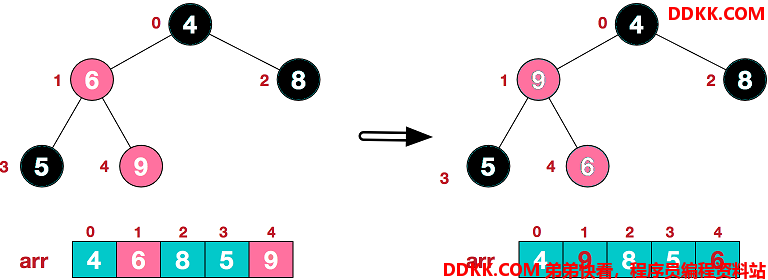
交换后,以倒数第一个非叶子结点的堆结构就调整好了。
第二步,调整倒数第二个非叶子结点,即第0个结点,该结点值为4。同样先找该结点的左右节点中值最大的子结点,这里是谁索引为1值为9的结点。然后判断该子结点是否大于该结点,9 >4,于是交换结点4和结点9。
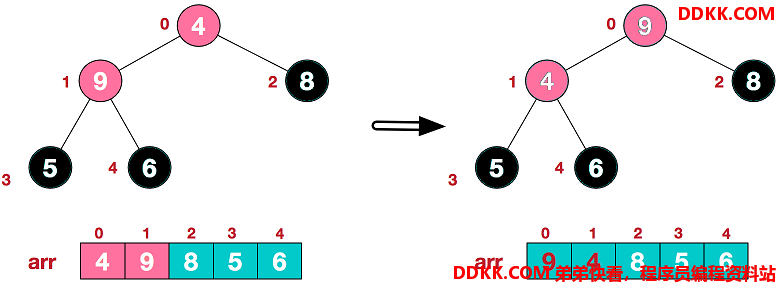
本来索引1结点对应子树已经调整为大顶堆结构,因为索引0结点发生交换,需要再一次调整索引0结点,使其对应子树为大顶堆。
循环以上步骤,直到调整完所有的非叶子结点。
要点:从最下边开始调整为大顶堆,如果一个结点调整后对应的子树已经为大顶堆,而其在后面没有被交换,那么这个结点到其对应的所有子结点都是大顶堆结构。比如这个例子中的第二步,如果索引0和索引1没有发生交换,那么我们是不用再倒回去调整索引1。
2.3 堆排序
假设待排序数组为arr,把它看成是顺序存储的二叉树,然后根据上面流程把该完全二叉树调整为大顶堆。此时arr的第一个元素就是最大值,把第一个元素和最后一个元素互换,这时最后一个元素为最大值。除去最后一个元素的arr子数组为arr1,对arr1继续调整为大顶堆,然后又交换arr1的首尾元素。如此反复进行交换、重建、交换。
3、代码实现
package cn.klb.datastructures.tree;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 实现堆排序(升序用大顶堆,降序用小顶堆)
* @Date: Create in 2023/4/14 19:52
* @Modified By:
*/
public class Heap {
/**
* 实现堆排序
* 降序排序,采用大顶堆
*/
public static void sort(int[] arr) {
// 把顺序存储二叉树调整为大顶堆
// 从最后一个非叶子结点开始,从下到上,从右到左遍历
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
// 对于调整好的大顶堆,最大元素在第一个位置
// 把第一个元素和最后一个元素互换,然后对不包括最大元素的剩余元素继续调整为大顶堆
// 知道剩下待调整元素剩下1个,即排序完毕
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
// arr去掉最后一个元素后的子数组为arr1,这个arr1除了第一个结点外,其他结点对应子树均满足大顶堆特性
adjustHeap(arr, 0, i);
}
}
/**
* 把以 arr[i] 为根结点所对应的子树调整为大顶堆
*
* @param arr 顺序存储二叉树
* @param i 第i个结点
* @param length 去掉上一轮排序完得到的最大值后剩下的有效结点个数
*/
private static void adjustHeap(int[] arr, int i, int length) {
// j=2*i+1 表示j是i的左子树
// for循环最后的 i = j 后,i就指向了它的子树,j = 2*j+1 为新的i对应的左子树
for (int j = 2 * i + 1; j < length; j = 2 * j + 1) {
// 选出最大值的子树
if (j + 1 < length && arr[j] < arr[j + 1]) {
j++;
}
// 如果当前结点的子结点比它大,则互换结点
if (arr[i] < arr[j]) {
swap(arr, i, j);
i = j; // 接着调整该子结点对应子树为大顶堆
} else {
// 因为一开始是从最后一个非叶子节点开始调整,所以当前二叉树的下边结点已经是大顶堆特性
// 如果互换,就破坏了子结点对应子树的大顶堆特性,需要继续向下调整
// 如果没有互换,就不会破坏子结点对应子树的大顶堆特性,就可以直接退出循环
break;
}
}
}
/**
* arr的 a和 b元素互换位置
*
* @param arr
* @param a
* @param b
*/
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
4、时间复杂度
O(nlogn)
5、稳定性
算法不能保证两个相同元素的前后顺序,因此是不稳定的。
6、测试
@Test
public void testHeap() {
int[] arr = new int[80000000];
for (int i = 0; i < 80000000; i++) {
arr[i] = (int) (Math.random() * 80000000);
}
SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
Date date1 = new Date();
System.out.println("-----" + sdf.format(date1) + "-----");
//System.out.println(Arrays.toString(arr));
Heap.sort(arr);
Date date2 = new Date();
System.out.println("-----" + sdf.format(date2) + "-----");
//System.out.println(Arrays.toString(arr));
// 8000万的随机数据进行堆排序,我的电脑花了大约27秒
}