1、介绍
分治算法的基本思想是把一个复杂的问题分成若干个相同或相似的子问题,再把子问题分解成更小的子问题,直到最后子问题可以简单地直接求解。原问题的解就是子问题的解的合并。这个技巧是很多高级算法的基础,比如排序算法中的快速排序、归并排序,还有傅里叶变换等。
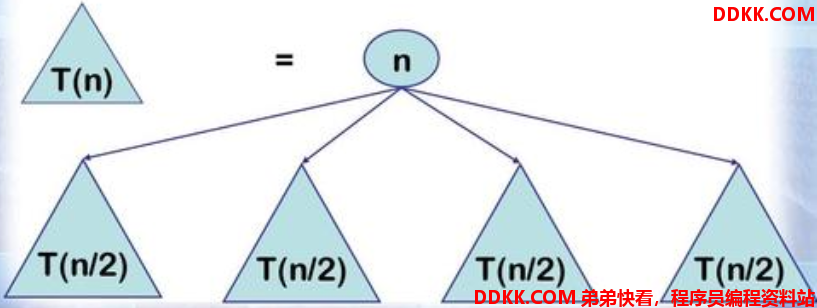
2、分治算法的设计模式

步骤为:
1、分解:把原问题分解为若干个规模较小的子问题,子问题相互独立;
2、解决:子问题很容易直接解决;
3、合并:把所有子问题的解合并为原问题的解。
3、最佳实践:汉诺塔
3.1 基本介绍
汉诺塔问题起源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上,从下到上按照顺序放着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按照大小顺序重新摆放在另一根柱子上。并且规定,小圆片上方不能放置大圆盘,在三根柱子之间一次只能移动一个圆盘。
假设每秒钟移动一次,共需要多少时间呢?移动完这些金片需要5845.54亿年以上,太阳系的预期寿命据说也就是数百亿年。真过那么久,地球上的一切早就灰飞烟灭了。
3.2 过程模拟
假设有一个汉诺塔如下图所示,总过三个圆盘,三根柱子分别为A、B、C:

第一步:A->C

第二步:A->B

第三步:C->B

第四步:A->C

第五步:B->A

第六步:B->C

第七步:A->C
游戏结束。
4、汉诺塔的分治归纳
如果只有一个圆盘,那就直接A->C即可。如果有两个圆盘,那么就得借助辅助柱子B,先A->B,然后A->C,最后B->C。
当圆盘的数量为3时,聪明的人还是可以拼出来。但是圆盘的数量不断增加时,就越来越难了。人都没办法搞定,代码就更没辙了。
当然,凡事都不能硬刚,都得有策略,仔细分析汉诺塔移动的过程,其实可以这样归纳:
1、当只有一个圆盘时,直接从起始柱子A移动到目的C柱子即可;
2、当有两个圆盘时,需要借助辅助柱子B,先把上面的圆盘放到辅助柱子B,然后把下面的柱子放到目的柱子C,然后再把辅助柱子的圆盘放到柱子C;
归纳:当有n(n>=2)个圆盘时,需要使用到辅助柱子B,先把除最后一个的柱子A所有圆盘放到辅助柱子B,然后把柱子A最后一个圆盘放到柱子C,最后把辅助柱子B的圆盘放到柱子C。
5、汉诺塔分治的代码实现
package cn.klb.algorithms.divideandconquer;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description: 递归实现汉诺塔游戏
* @Date: Create in 2023/4/19 10:59
* @Modified By:
*/
public class HanoiTower {
/**
* 输出汉诺塔小游戏所有过程
*
* @param num 盘子的数量
*/
public static void action(int num) {
// num数量的盘子要从A移动到C,借助辅助位置B
doAction(num, 'A', 'B', 'C');
}
/**
* 汉诺塔逻辑算法
*
* @param num 盘子个数
* @param a 盘子开始所在位置
* @param b 辅助位置
* @param c 盘子要移动到的目的位置
*/
private static void doAction(int num, char a, char b, char c) {
if (num == 1) {
// 如果只有一个盘子
System.out.println(a + "->" + c);
} else {
// 大于一个盘子
// 先把a位置除倒数最后一个盘子的全部盘子移动到位置b,把c当作辅助位置
doAction(num - 1, a, c, b);
// 然后把a位置最后一个盘子移动到c
System.out.println(a + "->" + c);
// 最后把b位置所有的盘子从b移动到c,把a当作辅助位置
doAction(num - 1, b, a, c);
}
}
}
6、测试类
package cn.klb.test.algorithmstest;
import cn.klb.algorithms.divideandconquer.HanoiTower;
import org.junit.Test;
/**
* @author DDKK.COM 弟弟快看,程序员编程资料站
* @Description:
* @Date: Create in 2023/4/19 11:07
* @Modified By:
*/
public class DivideAndConquerTest {
@Test
public void testHanoiTower(){
HanoiTower.action(3);
}
}
测试结果: