摘要
所有的图都是有最短路径的,计算最短路径比较经典的应用场景就是路径规划。最短路径也有它自身的局限性,比如不能出现负权环等。这里先了解最短路径的概况,后面几期将分别介绍求最短路径的几个经典算法。
在有权值的图中,可以找到最短路径,即指两顶点之间权值之和最小的路径,有向图和无向图都是可以找到最短路径的。如下图所示:
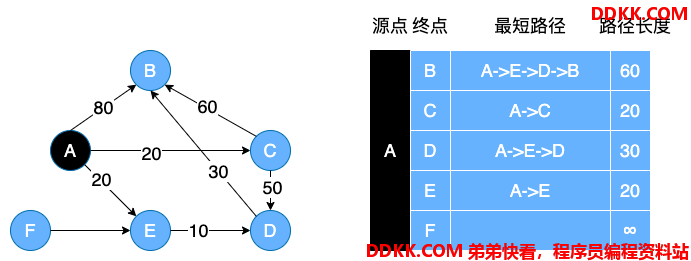
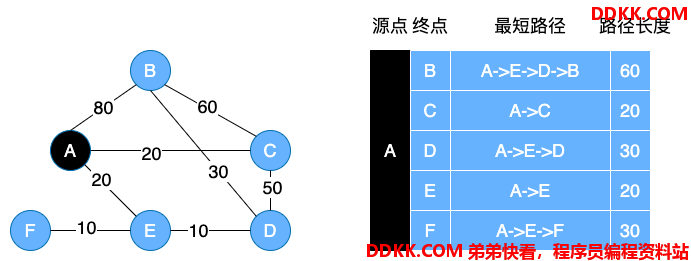
上面两个图就是有向图和无向图中顶点 A 到不同顶点的最短路径。
那么无权图有没有最短路径呢?答案也是有的。
无权图中的每一个边的权值可以想象成 1,那么每一个边的权值都是一样的。所以无权图的最短路径取决于该顶点到另外一个顶点途径边的数量。
负权边
有权图中,存在边的权值是负数时,被称为负权边。寻找图的最短路径中,是允许有负权边,但是不被允许存在负权环。因为负权环会让路径一直循环,权值一直无限递减下去,如下图所示:
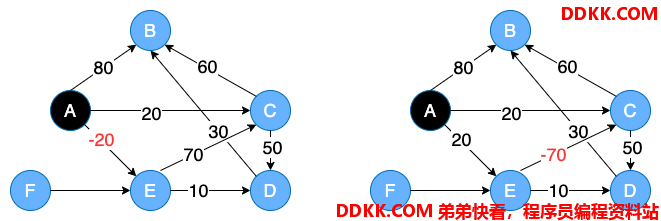
左侧图中,顶点A到顶点E是 -20,是被允许的。右侧图,顶点E到顶点C是-10,是不被允许的,因为顶点E、C、D 形成了一个环,并且是负权环(即三个边权值加起来是负值),在持续的循环下,权值会不断递减,是不合理的。
算法
应用最短路径最多的场景就是路径规划。处理最短路径的算法主要分为两类,一类是单源最短路径,就是确定一个顶点,求该顶点到其他边的最短路径。另外一类就是多源最短路径,就是可以求出任意的两个顶点之间的最短路径。不同的类别都对应的有经典的算法:
- 单源:Dijkstra(迪杰斯特拉算法)、Bellman-Ford(贝尔曼-福特算法)
- 多源:Floyd(弗洛伊德算法)
看算法的名称,就大概明白算法都是以发明者的名字来命名的。不同的算法都有各自的特点和局限性,在实际应用中要根据自己的需求来选择。最高级的是理解算法的逻辑,能够触类旁通,后面几期将分别介绍这几个算法。
总结
- 所有的图都是有最短路径的,不管有向图还是无向图;
- 图中的权值是允许存在负权边的,但是不允许存在负权环;
- Dijkstra、Bellman-Ford 和 Floyd 都是获取最短路径的经典算法;