摘要
今天通过一个求解斐波那契数列来看一下递归思想,在多个不同的优化过程中学习递归转换非递归的方式。
上期文章介绍了递归的本质,使用递归的思想等,今天通过一个案例来介绍使用递归的效果。这里就求解斐波那契数列。
斐波那契数列是 1、1、2、3、5、8、13、21、34、… 这么一组数列。这样有规律的数列,使用递归是最合适的了,先上代码:
int fib(int n) {
if (n <= 2) return n;
return fib(n-1) + fib(n-2);
}
代码中要特别注意 if (n <= 2) return n 这行代码,它就是递归基。通过代码可以推导出时间复杂度是 O(2n) ,空间复杂度是 O(n),尤其是空间复杂度,是看递归调用的深度以及需要创建的空间, fit 的调用过程如下图所示:
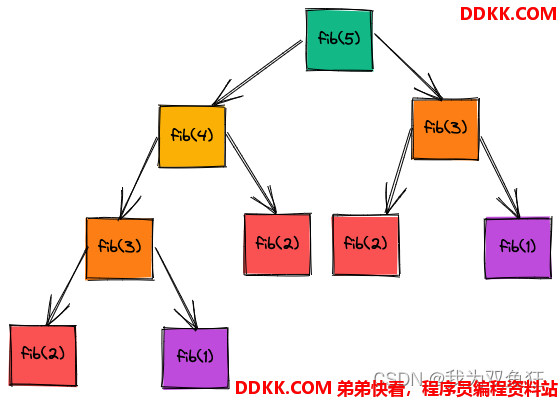
从图中可以看出,fib 的调用是从顶向下的,并且也可以看出其中有重复的计算。fib 的优化方向就有了,就是减少或者去除重复的计算。
优化1
fib的调用过程出现重复的计算,那么就可以使用数组来存储每次计算的结果,在调用过程中优先从数组中拿取已经存在的结果,如果没有结果再进行计算,代码如下:
int fib(int n) {
if (n <= 2) return 1;
int[] array = new int[n + 1];
array[2] = array[1] = 1
return fib(array, n);
}
int fib(int[] array, int n) {
if (array[n] == 0) {
array[n] = fib(array, n - 1) + fib(array, n - 2);
}
return array[n];
}
经过优化之后,函数的时间复杂度为 O(n),空间复杂度为 O(n),时间复杂度有较大的降低。
优化2
同时,上面的代码中,可以继续优化一下,就是将递归给去除,用 for 循环来处理,具体代码如下:
int fib(int n) {
if (n <= 2) return 1;
int[] array = new int[n + 1];
array[2] = array[1] = 1
for (int i = 3; i <= n; i++) {
array[i] = array[i-1] + array[i -2]
}
return array[n];
}
从for 循环可以看出,它的调用过程是从底到顶的顺序。时间复杂度和空间复杂度都是 O(n)。
优化3
如果仔细看优化2 中代码,会发现每次循环执行时,只会使用到 array 的其中两个元素,那么是不是可以用 array 只存放要用到的两个元素呢?下一个优化方向就清晰了,就是滚动数组方式来处理,具体代码如下:
int fib(int n) {
if (n <= 2) return 1;
int[] array = new int[2];
array[1] = array[0] = 1
for (int i = 3; i <= n; i++) {
array[i % 2] = array[(i-1) % 2] + array[(i -2) % 2]
}
return array[n % 2];
}
这时,fib 函数的时间复杂度是 O(n),但是空间复杂度就降低为 O(1)。看上面代码中,最主要的改动就是添加了 % 2(对 2 求模),针对这种求余方式可以更改为位运算,因为位运算比乘、除、模运算效率高很多。
那么% 2 用位运算替换为 & 1。因为这相当于任何数转换为二进制时,它和 1 做位运算时,只能得到 0 或者 1 这两个数,这是符合代码中需要的数字,所以可以这样处理。其他求模方式也可以按照这样的逻辑来推。
优化4
看优化3中使用滚动数组的方式来处理,数组中也只有两个元素,那么就可以更加简单,就直接创建两个变量来替换数组,即如下代码所示:
int fib(int n) {
if (n <= 2) return 1;
int first = 1;
int second = 1;
for (int i = 3; i <= n; i++) {
second = second + first;
first = second - first;
}
return second;
}
核心处理就是 for 循环中的处理,通过两个变量来获得结果并交换已知的结果。如果再添加一行代码 second = second - first,就完成了只需要 first 和 second 两个变量就互相交换了值。
优化5
斐波那契数列还有个线性代数解法,就是特征方程。
F( n ) = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] F(n) = \frac{1}{\sqrt{ 5 }}\left[ \left( \frac{1+\sqrt{ 5 }}{2} \right)^n - (\frac{1-\sqrt{ 5 }}{2})^n \right] F(n)=51[(21+5)n−(21−5)n]
代码如下所示:
int fib(int n) {
double c = Math.sqrt(5);
return (int)((Math.pow((1 + c) / 2, n) - Math.pow((1 - C) / 2, n)) / c);
}
使用特征方程实现,可以将函数的时间复杂度和空间复杂度降低到 O(logn),它主要取决于 pow 函数。
递归转非递归
在递归的调用过程中,会将每一次调用的参数、局部变量都保存在对应的栈中,如果调用的深度比较大时,会占用比较多的栈空间,容易造成栈溢出。那么就可以考虑递归转换成非递归(递归是可以 100% 的转换为非递归的)。
转换为非递归,首先可以想到的处理就是创建一个栈结构,自己维护栈结构和数据。因为递归调用会有比较多的重复变量,那么就可以删减重复的变量,让空间复杂度由 O(n) 降低为 O(1)。这就是递归转非递归的思路。
尾调用
尾调用就是一个函数的最后一个动作是调用函数,那么如果最后这个动作时调用自身,就被称为尾递归。
递归函数可以通过尾调用优化处理。后面会详细介绍如何优化。
总结
- 通过斐波那契数列案例来介绍递归思想;
- 递归可以 100% 转换为非递归;
- 递归函数本质就是创建一个栈来保存调用过程中的变量。