摘要
生成树是一种图的表现形式,它有个简单的规定,就是边的数量等于顶点的数量减一。在有权图中找到最小生成树在很多场景中被应用到。这里主要介绍一种获取最小生成树的方法,即 Prim。还有另外一种,下期继续。
生成树也被称为支撑树,在连通图中,它的极小连通子图就是生成树。极小连通子图包含连通图中全部的 n 个顶点,连接的边恰好只有 n-1 条(这里讨论无向图)。如下图所示的连通图:
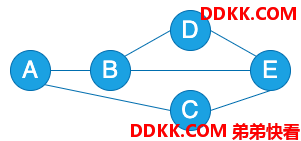
它的极小连通子图可以有如下3种(其实可以还有其他种):

看极小连通子图,可以总结出图中的顶点与边的关系为,边 = 顶点 - 1。
最小生成树
最小生成树通常也可以被称为最小权重生成树或者最小支撑树,即所有的生成树中,总的权值最小的那棵树。既然提到权重,那么最小生成树就是适用于有权的连通图(依然讨论的是无向的)。如下图所示,右侧部分就是最小生成树:
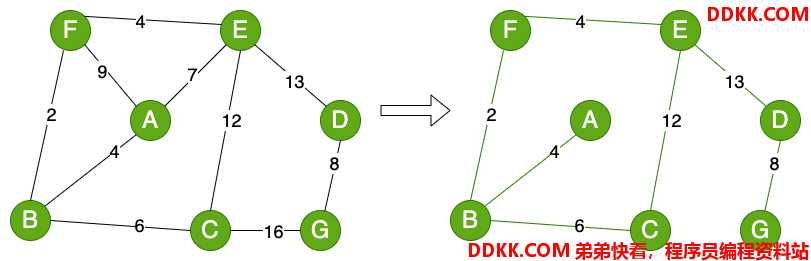
打个最小生成树应用的场景。假如要在多个城市之间铺设光缆,让它们之间可以通信。铺设光缆的费用比较高,而且每个城市之间的距离不同等等因素,造成不同城市之间铺设光缆的费用不同,如何以最低的费用铺设光缆呢?最小生成树就是解决的方案。
有一点要留意,在一个图中,每一条边的权值都互不相同,那么最小生成树只会有一个,否则可能会存在多个最小生成树。
现在求最小生成树有2个经典算法,分别是 Prim(普里姆算法)和 Kruskal(克鲁斯克尔算法)
Prim 算法
学习Prim 算法之前,需要了解切分定理,它是 Prim 定理的核心操作。
切分就是把图中的节点切分为两部分,这被称作一个切分,如下图所示:

这里将图切分成两部分,顶点 A、B、C 是一部分,D、E 是一部分。红色边被称为横切边,即一个边的两个顶点,分别属于切分的两部分,那么这个边就被称为横切边,如图 BD、BE、CE 就是横切边。
切分定理就是给定任意的切分,横切边中权值最小的边必定属于最小生成树。
Prim 算法执行时,假设一个有权的连通图(无向的)为 G(包含顶点和边),A 为 G 中的最小生成树。再定义一个存放顶点的集合 S,起始 S 中的顶点远小于 G 中的顶点。然后进行切分操作(后面提到),直到 S 和 G 中的顶点的数量相同。
切分操作是先找到切分 C = (S, V-S) 的最小横切边,并入到 A 中,同时将其顶点并入到集合 S 中,重复这样的操作。如下图所示(从左到右,从上到下,注意图中的几个元素,绿色的顶点、蓝色的顶点、黑色的边、绿色的边、红色的边、虚分割线、权值):

图中以顶点 B 开始进行切分,红色边就是横切边,绿色顶点部分是最小生成树集合。这里有几个核心操作:
1、 绿色顶点与蓝色顶点相连的边就是横切边,也是每次切分的部分;
2、 横切边中选择权值最小的,划分到绿色部分(最小生成树),然后将该边设置为绿色,权值相等,就随便选择一条边;
3、 当全部顶点都是绿色时,查看图中还是黑色的边,删除它,一个最小生成树就完成了;
先上代码,通过代码再来梳理一遍:
Set<EdgeInfo<V, E>> prim() {
Iterator<Vertex<V, E>> it = vertices.values().iterator();
if (!it.hasNext()) return null;
Vertex<V, E> vertex = it.next();
Set<EdgeInfo<V, E>> edgeInfos = new HashSet<>();
Set<Vertex<V, E>> addedVertices = new HashSet<>();
addedVertices.add(vertex);
MinHeap<Edge<V, E>> heap = new MinHeap<>(vertex.outEdges, edgeComparator);
int verticesSize = vertices.size();
while (!heap.isEmpty() && addedVertices.size() < verticesSize) {
Edge<V, E> edge = heap.remove();
if (addedVertices.contains(edge.to)) continue;
edgeInfos.add(edge.info());
addedVertices.add(edge.to);
heap.addAll(edge.to.outEdges);
}
return edgeInfos;
}
prim 函数返回的是 EdgeInfo 类型的集合,Edgeinfo 主要存放的是起始顶点、结束顶点和权值:
public static class EdgeInfo<V, E> {
private V from;
private V to;
private E weight;
public EdgeInfo(V from, V to, E weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
prim 函数中的前三行代码是保证图集合是否存在顶点,并获取第一个顶点,这里使用了迭代器的方式来处理(其他方式也可以):
Iterator<Vertex<V, E>> it = vertices.values().iterator();
if (!it.hasNext()) return null;
Vertex<V, E> vertex = it.next();
接下来创建存放 Edgeinfo 和存放最小生成树顶点的集合 addedVertices,存放第一个顶点,准备后面的切分操作。
这里使用 MinHeap 存放放入 addedVertices 中顶点的出度边,MinHeap 是小顶堆,会将其中的边按照权值,将最小的权值放在一个位置,后面再添加的边也会及时更新,一只保持权值最小的边在第一位(对小顶堆感兴趣可以看《数据结构与算法 - 基础(十九)堆》文章)。
MinHeap<Edge<V, E>> heap = new MinHeap<>(vertex.outEdges, edgeComparator);
最后就是不停将 heap 中权值最小的边拿出来,放入到 Edgeinfo 集合中,将边的结束顶点放入 addedVertices 中,再将结束顶点的边继续放入 heap 中。如果这个边的结束顶点已经在 addedVertices 中,就不做前面的操作。直到 addedVertices 中的顶点数量和图中的顶点数量相同结束。
也有一种情况,就是 heap 中的元素没有了,这时也是完成了,最后部分代码,看上面最开始的部分。
总结
- 生成树也被称为支撑树,图中的边数量等于顶点数量减一就可以被称为生成树,一个图中的生成树有很多;
- 最小生成树是权值最小总和最小的生成树,在权值互不相同的图中,最小生成树只有一个;
- Prim 是求最小生成树的算法,它使用切分的方式处理,其中用到小顶堆的数据结构。