摘要
递归是简化解决问题的思路,减少代码的处理方式。其本质就是将问题不断拆分成同类型的小问题,找到可以直接给出答案的地方时,再不断反推,直到得出原问题的答案。
递归(Recursion),就是函数直接或者间接调用自身,在编程中是非常常用的一种技巧。
比如下面代码中,就是直接调用自身:
int sum(int n) {
if (n < 1) return n;
return n + sum(n-1);
}
现象
举一个现实生活中的场景来理解递归。比如你坐在电影院的座位上,当你想知道自己现在坐的是第几排,你就可以问前一排(比如 A)做的是第几排,然后将结果加 1 就是自己想要的结果。
那么A 答复你等下,然后问他前一排(比如 B)做的是第几排,然后将结果加1就是 A 要回答的结果,接下来 B 像 A 一样…直到第一排的人告诉他做的是第一排。
最后从第一排开始,将结果一个个传递到你这,就完成了这次递归。
通过这个现象可以大致总结出递归的几个特性:
1、 A或者B获取第几排的逻辑是一样的;
2、 要有一个结束的点,即第一排就截止;
3、 当时不会有结果,需要等待;
调用过程
现在以下面的代码为例,梳理一下递归的调用过程:
public static void main(String[] args) {
sum(4);
}
private static int sum(int n) {
if (n <= 1) return n;
return n + sum(n -1);
}
递归的调用就像一个堆栈的数据结构,比如下图所示,就是上面代码的调用顺序。将每一次的计算先压入堆栈,全部压入完成之后,再依次取出处理。需要注意的是,每压入堆栈都需要创建空间去保存。
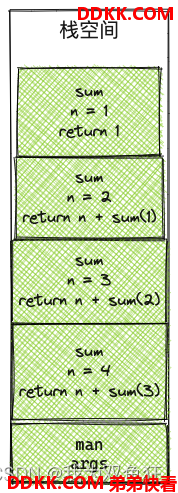
因为每次调用函数,都需要创建额外的空间,所以如果一直不终止递归,那么就一直消耗内存,最终导致内存溢出。
那么就必须要有一个终止条件,也就是结束递归的条件,也叫做边界条件或者递归基。
时间复杂度
先看一下调用过程中的代码,执行消耗的时间 T(n) = T(n-1) + O(1),所以它的时间复杂度是 O(n),空间复杂度是 O(n)。
依次求和也可以直接使用 for 循环来替代递归处理。有 n 个数相加,那就需要循环 n 次,在循环过程中不需要额外保存数据,所以它的时间复杂度是 O(n),但是空间复杂度是 O(1)。
还有更高效率的依次求和方法, 即高斯求和公式,如下面代码所示:
int sum(int n) {
if (n <= 1) return n;
return(n+1) * n >> 1;
}
通过代码可以看出它的时间复杂度为 O(1),空间复杂度也为 O(1)。
所以通过这三个求和的方式可以大致总结出,递归求出来的有可能是最优解,也有可能不是最优解。所以使用递归不是为了得到最优解,而是为了简化解决问题的思路,让代码更简洁。
基本思想
递归的基本思想总共分为拆解问题和求解这两部分:
- 拆解问题
1、 将规模大的问题拆解成规模较小的同类型问题;
2、 将规模较小的问题继续不断拆解成规模更小的同类型问题;
3、 规模小到一定程度可以直接得出它的答案;
-
求解
-
由最小规模的解求出较小规模问题的解;
-
由较小规模的解继续不断求出较大规模的解;
-
最后得出原来问题的解。
凡是可以用以上思路求解的问题,都可以使用递归来处理。很多链表、二叉树相关的问题都可以使用递归解决,因为链表、二叉树本身就是递归的结构。
使用递归
使用递归时,需要明确这3个步骤:
1、 明确函数的功能,即先要搞清楚函数干什么,不要纠结代码应该怎么写;
2、 明确原问题和子问题的关系,即找出f(n)与f(n-1)的关系;
3、 明确边界条件(即递归基),即思考问题规模小到什么程度就可以直接得出解;
总结
- 递归就是自己调用自身;
- 基本思路就是拆解问题,然后求解;
- 递归必须要明确递归基,即边界条件来结束,否则会一直被调用,导致内存溢出。