摘要
在上期介绍完无向图和有向图之后,延伸出完全图、有权图以及连通图。主要根据边直接连接,还是间接连接,有方向,还是没有方向来区分。其中的有权图在实际生活中可以找到很多对应的场景。
上期文章介绍了图的概念,有向图、无向图、简单图和复杂图这几个分类。本期要继续深入地介绍图的几个分类。
无向完全图
无向图的任意两个顶点之间都存在边时,称为无向完全图。在无向完全图中,顶点和边的关系为:n 个顶点有 n(n-1)/2 条边。
如下图所示,边可以用顶点表示的公式:1 + 2 + 3 + … + (n-3) + (n-2) + (n-1)

有向完全图
有向图的任意两个顶点之间都存在方向相反的两条边,称为有向完全图。结合无向完全图的定义,有向完全图比无向完全图多一倍的边,所以顶点和边的关系为:n 个顶点有 n(n-1) 条边。

以完全图为标准,可以分类出稠密图和稀疏图:
稠密图:边数接近于或等于完全图
稀疏图:边数远远少于完全图
有权图
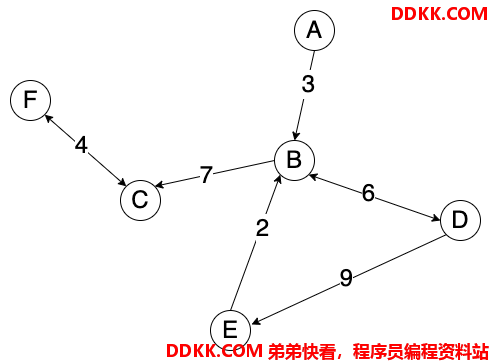
当边上存在权值的图就是有权图。有权图在很多场景中被应用,比如导航找出时间最少的路线,找到最少交高速费的路线,几个村之间修路,根据人口等设计连接等。
要特别注意,有权图中的边可以是有方向的、也可以是没有方向的,也可以是既有方向,也可以是没有方向的,如下图所示:
连通图
在一个图中,假如顶点 x 和 y 之间存在可相互抵达的路径(直接或者间接的),则认为 x 和 y 是连通的。
那么,如果在无向图中,任意2个顶点都是连通的,就称为该图为连通图。如下图所示,都是连通图:
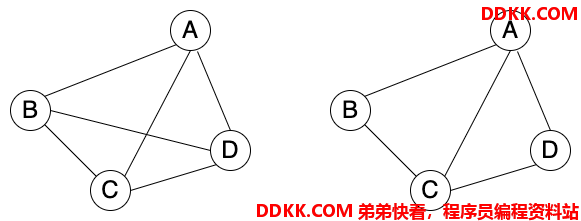
在连通图中,也要介绍一下连通分量,连通分量就是无向图中最大的连通子图。在连通图中,它只有一个连通分量,就是它本身,如果是非连通的无向图,就会存在多个连通分量。
强连通图
连通图是基于无向图的定义,即连通图的边是无向的,当把无向的边更换为有向的,就是强连通图。
所以,强连通图就是有向图中的任意两个顶点都是连通的,如下图所示:
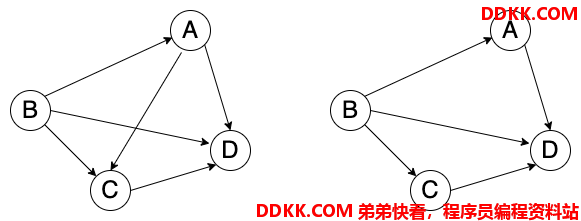
在强连通图中,也有强连通分量,强连通分量就是有向图中最大的强连通子图。在强连通图中只有一个强连通分量,就是自身。如果是非连通的有向图,就会存在多个强连通分量。
总结
- 当任意顶点之间都有边(直接连接)存在的图,就是完全图,分为无向完全图和有向完全图;
- 当边存在权值的图,就是有权图,有权图的实际应用场景非常多;
- 当任意两个顶点都可以连接(直接或者间接),就是连通图;
- 根据边是否有方向,判断出连通图和强连通图,并对应的有连通分量。