摘要
实现图结构的方案大致为邻接矩阵和邻接表,本期就介绍一下这两个方案分别是什么。在最后会处理一下图的基本接口,以及顶点结构和边结构,为下期代码实现做准备。
前两期文章介绍了图的基本概念,以及图的种类。这期就了解一下实现图结构的方案。主要有两种实现方案,分别是邻接矩阵和邻接表。
邻接矩阵
邻接矩阵就是用数组来分别存放顶点和边。即用一个一维数组存放顶点,用一个二维数组存放边。
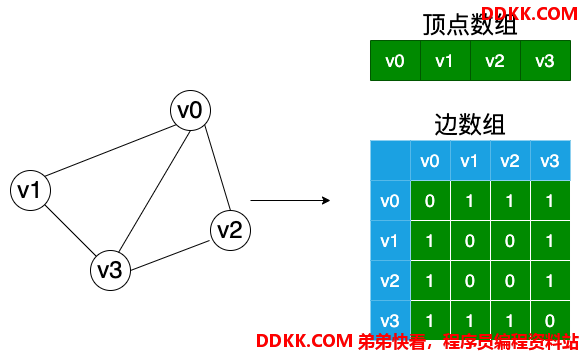
上图可以看出,使用邻接矩阵描述一个无向图时,若两个顶点连接,就设置为 1,反之,就设置为 0。
那么有向图,该怎么表示呢?
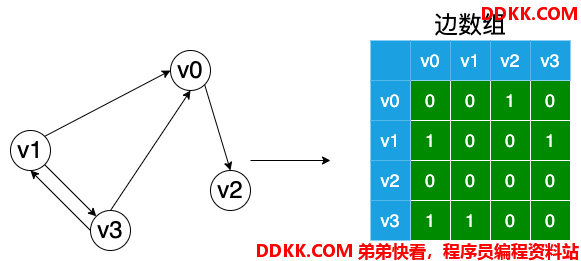
上图可以看到,有向图的邻接矩阵从左侧看,分别可以知道某一个顶点到其他顶点的连接情况,比如顶点 v1 和顶点 v3 的连接情况,就可以看到左侧 v1 和顶部 v3 的交汇点数字为 1,左侧 v3 和顶部 v1 的交汇点数字为 1,这就表示图中 v1 和 v3 相关连接的关系。
最后就是有权图该如何表示呢?
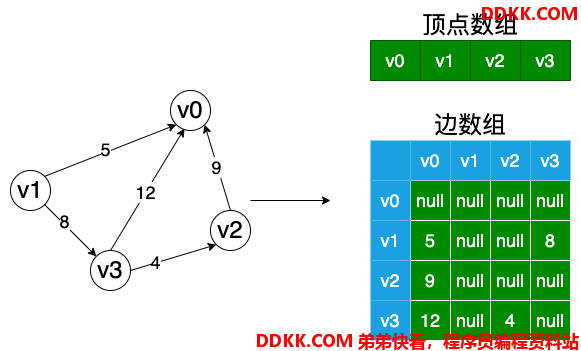
有权图的邻接矩阵和有向图的邻接矩阵很相似,有两个区别点:
1、 当一个顶点到另外一个顶点有连接,交汇的点填写权值;
2、 那么这个顶点到另外一个顶点没有连接,交汇点填写null(或者其他符合都可以);
邻接表
邻接表就类似哈希表,即把所有顶点都依次放到一个数组里面,然后拿到第一个顶点,找到和它连接的顶点,像火车车厢一样,一个个的指向它们。直到最后一个没有可以指向的顶点时,就用 null 来表示(或者其他的符号)。

图中箭头指向,表示要将指向的顶点放在上一个空格的位置,接下来表示有向图时,如下图:

表示有权图时,可以将权值放在指向的下一个顶点中,如下图:

基础接口
接下来,就开始用代码来实现图结构。这里先定义一下图结构的接口 API,包括添加或者删除顶点,添加或者删除边等。
// 顶点数量
int verticesSize();
// 边数量
int edgesSize();
// 添加顶点
void addVertice(V v);
// 移除顶点
void removeVertice(V v);
// 添加边
void addEdge(V fromV, V toV);
// 添加边,包括权值
vode addEdge(V fromV, V toV, E weight);
// 移除边
void removeEdge(V fromV, V toV);
定义顶点
在开始之前,需要先了解出度和入度这两个名词:
- 出度:一个顶点的出度为 x,是指有 x 条边以这个顶点为起点;
- 入度:一个顶点的入度为 x,是指有 x 条边以该顶点为终点;
在一个顶点中需要记录出度的边,也要记录入度的边,因为顶点上有多个边,所以需要用列表结构来存储,还需要记录元素。自定义一个顶点比较的方法,来确定顶点是否相同。最后重写一下 获取顶点哈希值的方法,留作备用。
private static class Vertex<V, E> {
V value;
// 进来的边
Set<Edge<V, E>> inEdges = new HashSet<>();
// 出去的边
Set<Edge<V, E>> outEdges = new HashSet<>();
// 构造方法
Vertex(V v) {
this.value = v;
}
// 自定义对比和 hash code
@Override
public boolean equals(Object obj) {
return Objects.equals(value, ((Vertex<V, E>)obj).value);
}
@Override
public int hashCode() {
return value == null ? 0 : value.hashCode();
}
}
定义边
边结构中要记录起始和结束的顶点,一个边只能有一个起始顶点和一个结束顶点,这里也要提前定义记录权值的属性。在结构中要重写是否相同的方法,重写边的哈希值留作后用。
private static class Edge<V, E> {
// 起点
Vertex<V, E> from;
// 终点
Vertex<V, E> to;
// 权值
E weight;
Edge(Vertex<V, E> from, Vertex<V, E> to) {
this.from = from;
this.to = to;
}
EdgeInfo<V, E> info() {
return new EdgeInfo<>(from.value, to.value, weight);
}
// 实现对比和 hash code
@Override
public boolean equals(Object obj) {
Edge<V, E> edge = (Edge<V,E>)obj;
return Objects.equals(from, edge.from) && Objects.equals(to, edge.to);
}
@Override
public int hashCode() {
return from.hashCode() * 31 + to.hashCode();
}
}
代码中可以看出,在 equals 方法中,要同时满足起始顶点、结束顶点相等,这个边才相等。在 hashCode 中的 *31 是将起始顶点的哈希值放在高位(向左移动了5个位置,二进制),和结束顶点的哈希值组合得来的。
总结
- 图的两个实现方案分别是邻接矩阵和邻接表;
- 图的基本接口是顶点和边的数量,添加和删除顶点,添加和删除边,这3项;
- 顶点的结构中要分别记录出度和入度的边,以及元素;
- 边的结构中要分别记录起始顶点和结束顶点;
- 不论是顶点结构还是边结构,都要重写 equals 和 hashCode 这两个方法。