数据结构与算法 - 实战：图的遍历

摘要

图的遍历有两种方式，这两种方式和二叉树的层序遍历和前序遍历逻辑是一致的，在实现过程中使用到了队列和栈的数据结构。看本期文章相当于重温一下队列、栈和二叉树的遍历等知识。

从图中某一个顶点出发访问图中其余的顶点，并且一个顶点只能被访问一次，这样的过程就是图的遍历。因为图中存在有向边，所以图中的顶点并不是一定会被访问到，而且在代码实现的时候，要专门过滤已经访问过的顶点。

通常图的遍历有两个方案，一种是广度优先搜索（Breadth First Search, BFS），另外一种是深度优先搜索（Deapth First Search, DFS）。这两种方案和二叉树的层序遍历和前序遍历有很多相似的地方，感兴趣的话，可以看《数据结构与算法 - 基础（二十二）二叉树的非递归遍历》文章。

广度优先搜索（BFS）

广度优先搜索相当于一层一层的遍历，先访问这个顶点直接相连的顶点，再访问直接相连顶点的直接相连顶点，直到没有可以被访问的顶点为止。

如果是有向图，那么只能访问这个顶点指向的顶点，不可以访问指向自己的顶点。

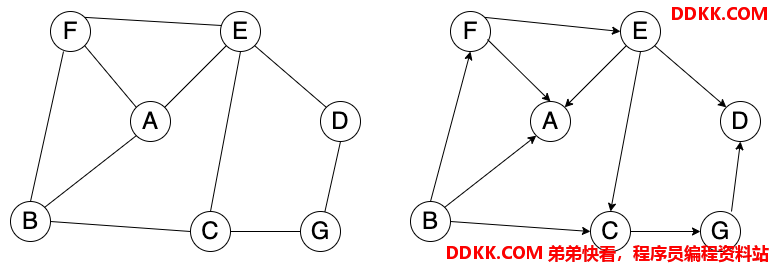
如上图所示，左侧是无向图，右侧是有向图。以顶点 F 为例，分别在有向图和无向图中的广度优先搜索的顺序如下表：

层级	无向图	有向图
第一层	F	F
第二层	B、A、E	A、E
第三层	C、D	C、D
第四层	D	G

看表中的有向图访问顺序，可以看到顶点 B 没有被访问到，这也呼应文章开始的结论，图中的顶点不是一定会被访问到。

代码上可以使用队列存放即将被遍历的顶点，当每访问一个顶点，就将该顶点的出度边连接的顶点存放在队列中，队列的 FIFO 特性就可以保证每一层能够完全被访问到（这和二叉树的层序遍历逻辑一致），代码如下：

public void bfs(V begin) {
   
     
    Vertex<V, E> beginVertex = vertices.get(begin);
    if (beginVertex == null) return;

    // 保存已经入队的，即会被访问到的顶点
    Set<Vertex<V, E>> visitedVertices = new HashSet<>();
    // 队列
    Queue<Vertex<V, E>> queue = new LinkedList<>();
    queue.offer(beginVertex);
    visitedVertices.add(beginVertex);
    while (!queue.isEmpty()) {
   
     
        Vertex<V, E> vertex = queue.poll();
        System.out.println(vertex.value);
        for (Edge<V, E> edge : vertex.outEdges) {
   
     
            if (visitedVertices.contains(edge.to)) continue;
            queue.offer(edge.to);
            visitedVertices.add(edge.to);
        }
    }            
}

代码中可以看到，visitedVertices 中存放已经入队的顶点，在下面查找顶点中过滤掉已经入队的顶点，防止重复访问同一个顶点。还有需要留意的点，就是入队的都是出度集合中边的结束顶点，这个边的起始顶点就是自身，所以没有必要再入队。

深度优先搜索（DFS）

深度优先搜索，就是按照一个路径访问它的顶点，直到没有可以被访问的顶点时，就切换到另外一条路径继续访问，这个逻辑和二叉树的前序遍历是一样的，如下图中无向图和有向图：

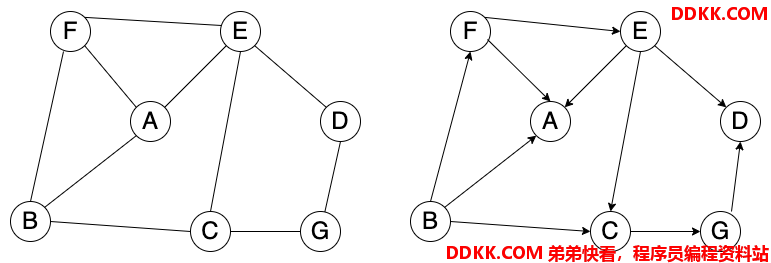
左侧是无向图，右侧是有向图，如果使用深度优先搜索访问这两个图，大致的顺序如下：

无向图：F、B、C、G、D、E、A

有向图：F、E、D、C、G、A

上面的访问结果肯定不是唯一的，你也可以找出其他访问的顺序。主要思想就是沿着一条路走到黑，然后再换其他的路继续走到黑。

实现的代码中，和广度优先搜索一样的就是创建一个集合存放将要被访问的顶点，避免重复访问。与其不同的是，这里使用栈的数据结构来访问顶点。

public void dfs(V begin) {
   
     
    Vertex<V, E> beginVertex = vertices.get(begin);
    if (beginVertex == null) return;
    Set<Vertex<V, E>> visitedVertices = new HashSet<>();
    Stack<Vertex<V, E>> stack = new Stack<>();

    // 遍历第一个
    if (visitor.visit(begin)) return;
    visitedVertices.add(beginVertex);
    stack.push(beginVertex);

    // 遍历接下来的
    while (!stack.isEmpty()) {
   
     
        Vertex<V, E> vertex = stack.pop();
        for (Edge<V, E> edge : vertex.outEdges) {
   
     
            if (visitedVertices.contains(edge.to)) continue;

            stack.push(edge.from);
            stack.push(edge.to);
            System.out.println(vertex.value);
            visitedVertices.add(edge.to);
            break;
        }
    }    
}

代码中遍历栈中的顶点时，依然是拿出顶点的出度边集合中，边的结束顶点压入栈中。需要留意的点是，在压入结束顶点之前会先压入起始顶点。是因为保证可以遍历完起始顶点的所有边，这个起始顶点已经放在将要访问的顶点集合中，也不用担心会重复遍历它。

既然类似二叉树的前序遍历，那么另外一种遍历的实现方式也是可行的，那就是递归的方式进行遍历：

void dfs(Vertex<V, E> vertex, Set<Vertex<V, E>> visitedVertices) {
   
     
    System.out.println(vertex.value);
    visitedVertices.add(vertex);

    for (Edge<V, E> edge : vertex.outEdges) {
   
     
        if (visitedVertices.contains(edge.to)) continue;
        dfs(edge.to, visitedVertices);
    }
}

总结

图的遍历方式有两种，一种是广度优先搜索，另外一种是深度优先搜索；
广度优先搜索是基于队列的结构实现，类似二叉树的层序遍历；
深度优先搜索是基于栈的数据结构实现，类似二叉树的前序遍历；
为了保证顶点只会被访问一次，需要额外创建一个集合存放将要被访问的顶点。

07、数据结构与算法 - 实战：图的遍历

广度优先搜索（BFS）

深度优先搜索（DFS）

总结