题目地址:https://leetcode-cn.com/problems/course-schedule-iv/
题目描述
你总共需要上 n 门课,课程编号依次为 0 到 n-1 。
有的课会有直接的先修课程,比如如果想上课程 0 ,你必须先上课程 1 ,那么会以 [1,0] 数对的形式给出先修课程数对。
给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。
对于每个查询对 queries[i] ,请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。
请返回一个布尔值列表,列表中每个元素依次分别对应 queries 每个查询对的判断结果。
注意:如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程,那么课程 a 也是课程 c 的先修课程。
示例1:
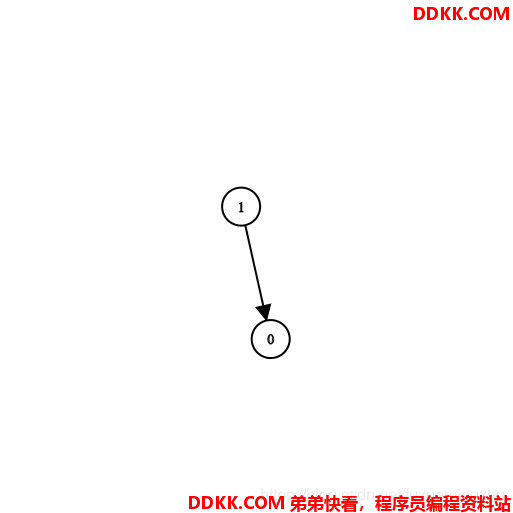
输入:n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出:[false,true]
解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例2:
输入:n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出:[false,false]
解释:没有先修课程对,所以每门课程之间是独立的。
示例3:
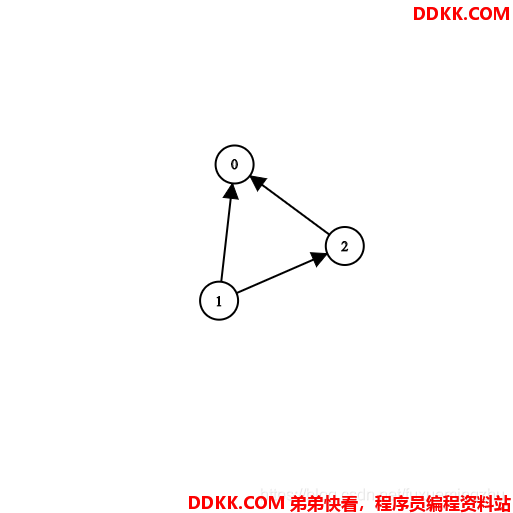
输入:n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出:[true,true]
示例4:
输入:n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出:[false,true]
示例5:
输入:n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出:[true,false,true,false]
提示:
1、2<=n<=100;
2、0<=prerequisite.length<=(n*(n-1)/2);
3、0<=prerequisite[i][0],prerequisite[i][3]<n;
4、prerequisite[i][0]!=prerequisite[i][4];
5、 先修课程图中没有环;
6、 先修课程图中没有重复的边;
7、1<=queries.length<=10^4;
8、queries[i][0]!=queries[i][5];
题目大意
题目给出了一个图。判断是否可以从queries[i][0]走向queries[i][1]。
解题方法
DFS
检查有向图中从queries[i][0]出发是否可以到达queries[i][1],最简单的思路就是 DFS 看到能否搜索到。但是看了题目给出的数量级,估算如果每次query都在全图 DFS 搜索,时间复杂度为 O(queries.length * prerequisite.length) 约为 10^8 量级,则会超时。
那么DFS 就不行了吗?并不见得。我们可以看出 DFS 会存在同一路径重复查找的现象,可以进行优化。
举例说明,假如题目给出的先修课程的图是这样的:
1 -> 2 -> 3 -> 4
假如第一个 query 判断了 1 -> 4 是可以的; 假如第二个 query 要判断 2 -> 4,是否需要重新搜索一遍呢?我们在第一个query中已经走过了这条路了呀,就没有必要重新搜索了。
即,我们的思路就是记录已经判断过的所有的路径,防止重复计算。比如在上面的例子中,我们在搜索 1 -> 4 的过程中,保存记录 1,2,3 都可以走到 4;如果下次再判断 2 是否能到 4 的时候,就可以在O(1)的时间内直接出结果了。
代码的实现时,先写出普通的 DFS 搜索是否可从 start 到达 end 的代码,然后可以用 Python3 提供的@functools.lru_cache,该函数能自动保存函数的参数和返回,相当于函数调用的记忆化。如果不用该函数,也可以自己定义memo数组来记录参数和返回。
- 时间复杂度:最好情况下只需要第一次搜索的时候把路径保存下来,之后查表就行,因此时间复杂度是 O(n);最坏情况下,查询的时候从来没有走过重复的路径(比如星型的图),时间复杂度是O(N * queries.length)。
- 空间复杂度:最省空间的时候是没有保存过重复的路径,空间复杂度是O(1);最费空间是把所有的节点两两路径保存,空间复杂度是O(N^2)。
Python 代码如下:
class Solution(object):
def checkIfPrerequisite(self, n, prerequisites, queries):
"""
:type n: int
:type prerequisites: List[List[int]]
:type queries: List[List[int]]
:rtype: List[bool]
"""
self.graph = collections.defaultdict(list)
for pre in prerequisites:
self.graph[pre[0]].append(pre[1])
return [self.dfs(query[0], query[1]) for query in queries]
start -> end ?
@functools.lru_cache
def dfs(self, start, end):
if start == end:
return True
return any(self.dfs(nxt, end) for nxt in self.graph[start])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发