题目地址:https://leetcode-cn.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/
题目描述
n座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
示例1:
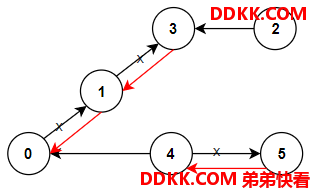
输入:n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出:3
解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例2:

输入:n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出:2
解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例3:
输入:n = 3, connections = [[1,0],[2,0]]
输出:0
提示:
1、2<=n<=5*10^4;
2、connections.length==n-1;
3、connections[i].length==2;
4、0<=connections[i][0],connections[i][1]<=n-1;
5、connections[i][0]!=connections[i][1];
题目大意
要让所有节点都能到达 0 节点,需要翻转多少个边?
解题方法
题目问的是所有顶点都能到节点 0 要翻转多少边。可以反过来,求从节点 0 出发到达所有顶点需要翻转多条边,于是就把多源问题转化成了单源问题。
但题目给出的是单向图,由于箭头是有向的,导致无法从节点 0 出发到达所有顶点。因此为了能让从节点 0 出发到达所有顶点,于是我们把单向图改成双向图,并且赋予不同的边不同的权重:题目给出的边的权重都是 1,我们添加的反向的边,权重都是 0 。
这样的目的是:我们从节点 0 出发,如果沿着题目给出的边走,权值为 1,即最终需要反向该边;如果沿着我们新添加的边走,权值为 0,即最终不需要反向该边。
如下图所示,直线是题目原本给出的边,权值为 1;曲线是自己添加的边,权值为 0。如果从节点 0 出发,需要沿着红色的路径,把所有的节点遍历一遍。累加次红色路径上所有的权值为 3,即如果让所有的点都能到达节点 0 ,需要翻转 3 条边。 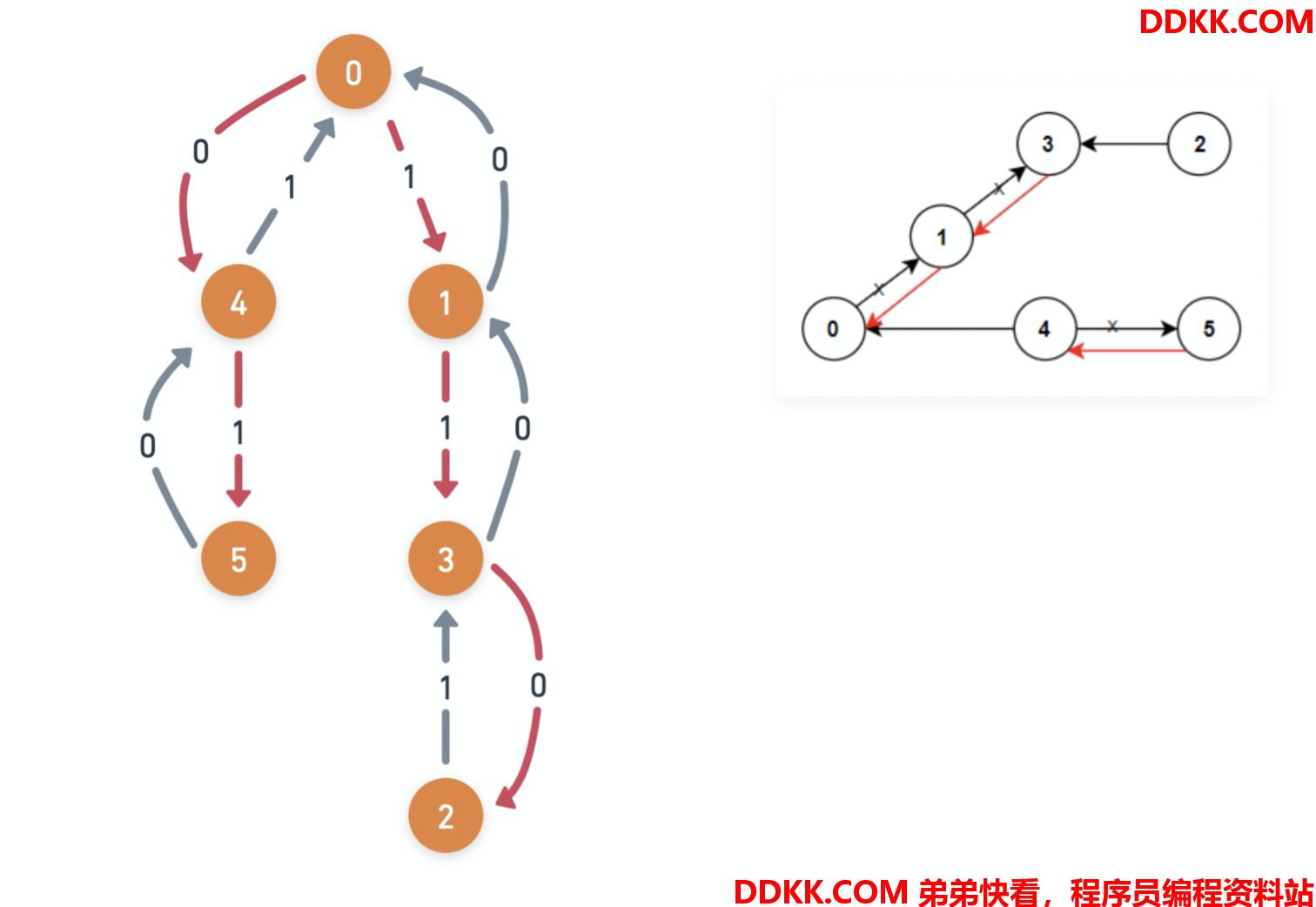
遍历过程可以用 DFS 或者 BFS 两种做法完成。
DFS
记得需要使用 visited 保存已经遍历过的顶点,防止重复访问。
Python 代码如下:
class Solution:
def minReorder(self, n: int, connections: List[List[int]]) -> int:
graph = collections.defaultdict(dict)
for con in connections:
graph[con[0]][con[1]] = 1
graph[con[1]][con[0]] = 0
visited = set()
return self.dfs(graph, 0, visited)
def dfs(self, graph, cur, visited):
res = 0
visited.add(cur)
for nxt, value in graph[cur].items():
if nxt not in visited:
res += value
res += self.dfs(graph, nxt, visited)
return res
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
BFS
记得需要使用 visited 保存已经遍历过的顶点,防止重复访问。
class Solution:
def minReorder(self, n: int, connections: List[List[int]]) -> int:
graph = collections.defaultdict(dict)
for con in connections:
graph[con[0]][con[1]] = 1
graph[con[1]][con[0]] = 0
queue = collections.deque()
queue.append(0)
visited = set()
res = 0
while queue:
cur = queue.popleft()
visited.add(cur)
for nxt, value in graph[cur].items():
if nxt not in visited:
res += value
queue.append(nxt)
return res
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发