题目地址:https://leetcode-cn.com/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts/
题目描述
矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离,类似地, verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果对 10^9 + 7 取余后返回。
示例1:

输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出:4
解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
示例2:
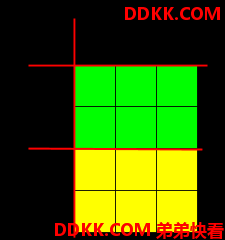
输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出:6
解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。
示例3:
输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出:9
提示:
1、2<=h,w<=10^9;
2、1<=horizontalCuts.length<min(h,10^5);
3、1<=verticalCuts.length<min(w,10^5);
4、1<=horizontalCuts[i]<h;
5、1<=verticalCuts[i]<w;
6、 题目数据保证horizontalCuts中的所有元素各不相同;
7、 题目数据保证verticalCuts中的所有元素各不相同;
题目大意
本题给出了一个矩形,并给出了横竖很多切割线,求切割得到最大矩形面积。
解题方法
找最大间隔之积
第一想法是暴力:对每个横竖切割线两两组合,求出组合出的所有矩形的最大的面积。该方法的时间复杂度是 O(M * N),M 和 N 分别为横竖切割线的个数,看了题目给出的 M 和 N 都是 10^5 量级,想乘就是 10^10 量级,会超时。
既然不能暴力求解,就必须优化。稍加思索,不难想到:找出切割线中 最大行间隔 和 最大列间隔,两者相乘就是最大矩形面积。
原因是:每一个 行间隔 都跟所有的 列间隔 相交,每一个 列间隔 也都跟所有的 行间隔 相交,而且他们都是正数。
用数学表述就是在
1、1<=horizontalCuts[i]<=max(horizontalCuts),;
2、1<=verticalCuts[j]<=max(verticalCuts);
两个条件的约数下,求 horizontalCuts[i] * verticalCuts[j] 最大值。
显然答案是 max(horizontalCuts) * max(verticalCuts)。
在实现的时候添加了矩形的边界[0, h], [0, w],对 行列的切割线 进行了排序,然后遍历求 行列的切割间隔 最大值,最后求行列最大值的乘积。
最后,注意题目要求对 10^9 + 7 取余。
Python 代码如下:
class Solution:
def maxArea(self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]) -> int:
horizontalCuts.append(0); horizontalCuts.append(h)
verticalCuts.append(0); verticalCuts.append(w)
horizontalCuts.sort()
verticalCuts.sort()
M, N = len(horizontalCuts), len(verticalCuts)
max_hc = 0
max_vc = 0
for i in range(M - 1):
max_hc = max(max_hc, horizontalCuts[i + 1] - horizontalCuts[i])
for j in range(N - 1):
max_vc = max(max_vc, verticalCuts[j + 1] - verticalCuts[j])
return (max_hc * max_vc) % (10 ** 9 + 7)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
DDKK.COM 弟弟快看-教程,程序员编程资料站,版权归原作者所有
本文经作者:负雪明烛 授权发布,任何组织或个人未经作者授权不得转发