数据结构
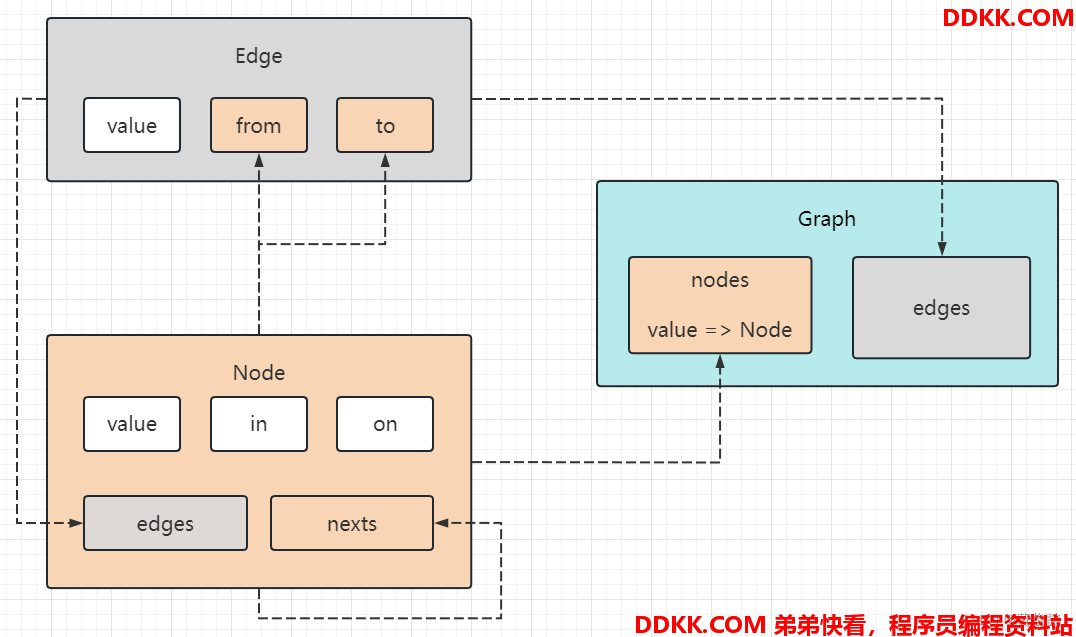
点
/**
* 图中的点
* Created by huangjunyi on 2022/8/30.
*/
public class Node {
//点的值
public int value;
//入度
public int in;
//出度
public int out;
//从该节点出发,能找到的邻居节点集合
public List<Node> nexts;
//从该节点出发,能到的邻居节点的边的集合
public List<Edge> edges;
public Node(int value) {
this.value = value;
this.in = 0;
this.out = 0;
this.nexts = new ArrayList<>();
this.edges = new ArrayList<>();
}
}
边
/**
* 图中的边
* Created by huangjunyi on 2022/8/30.
*/
public class Edge {
//边的权重
public int value;
//边的起始点
public Node from;
//边的终点
public Node to;
public Edge(int value, Node from, Node to) {
this.value = value;
this.from = from;
this.to = to;
}
}
图
/**
* 图结构
* Created by huangjunyi on 2022/8/30.
*/
public class Graph {
//图中所有的点
public Map<Integer, Node> nodes;
//图中所有的边
public Set<Edge> edges;
public Graph() {
this.nodes = new HashMap<>();
this.edges = new HashSet<>();
}
}
给定一个样本集,初始化一个图结构
/**
* 给定一个样本集,初始化一个图结构
* Created by huangjunyi on 2022/8/30.
*/
public class Graph01 {
public static Graph create(int[][] samples) {
Graph graph = new Graph();
for (int[] sample : samples) {
int value = sample[0]; //边的权重
int from = sample[1]; //边的起始点的值
int to = sample[2]; //边的终点的值
//如果图中不包含该点,则添加
if (!graph.nodes.containsKey(from)) {
graph.nodes.put(from, new Node(from));
}
//如果图中不包含该点,则添加
if (!graph.nodes.containsKey(to)) {
graph.nodes.put(to, new Node(to));
}
//从图中取出边的起始点
Node fromNode = graph.nodes.get(from);
//从图中取出边的终点
Node toNode = graph.nodes.get(to);
//构建边
Edge edge = new Edge(value, fromNode, toNode);
//把终点添加到起始点的邻居节点集合中
fromNode.nexts.add(toNode);
//起始点的出度+1
fromNode.out++;
//把边放入起始点
fromNode.edges.add(edge);
//终点入度+1
toNode.in++;
//把边放入图中
graph.edges.add(edge);
}
return graph;
}
}
图的广度优先遍历
- 队列 + set
- 队列用于放入待遍历的节点
- set记录一个节点是否遍历过,遍历过的节点不再入队列
- 一直遍历,直到队列为空
/**
* 图的广度优先遍历
* Created by huangjunyi on 2022/8/30.
*/
public class Graph02 {
public static void bfs(Node node) {
if (node == null) {
return;
}
// 队列用于放入待遍历的节点
Queue<Node> queue = new LinkedList<>();
// set记录一个节点是否入过队列,是则不再入队列
Set<Node> set = new HashSet<>();
// 头节点入队列
queue.offer(node);
// 记录头已经入过队列
set.add(node);
// 一直遍历,直到队列为空
while (!queue.isEmpty()) {
// 从队列弹出节点,打印
Node curr;
System.out.println((curr = queue.poll()).value);
// 看该节点是否有没有入过队列的节点,有则入队列,等待遍历
for (Node next : curr.nexts) {
if (!set.contains(next)) {
queue.offer(next);
set.add(next);
}
}
}
}
}
图的深度优先遍历
- 栈 + set
- 栈用于存储遍历过的节点,沿着节点路径一直往里遍历,遍历到的节点放入栈中
- set记录遍历过的节点,一个节点遍历过,就不在入栈
- 如果走到尽头了,从栈中弹出栈顶节点,继续遍历弹出节点的其他没有遍历过的邻居
- 一直遍历直到栈为空
/**
* 图的深度优先遍历
* Created by huangjunyi on 2022/8/30.
*/
public class Graph03 {
public static void dfs(Node node) {
if (node == null) {
return;
}
// 栈用于存储遍历过的节点,沿着节点路径一直往里遍历,遍历到的节点放入栈中
Deque<Node> stack = new LinkedList<>();
// set记录遍历过的节点,一个节点遍历过,就不在入栈
Set<Node> set = new HashSet<>();
// 入栈前先打印,表示已经遍历过
System.out.println(node.value);
// 头节点入栈
stack.push(node);
// 记录头节点遍历过
set.add(node);
// 一直遍历直到栈为空
while (!stack.isEmpty()) {
// 从栈中弹出栈顶节点,遍历弹出节点的邻居,把没有遍历过的邻居节点入栈
Node curr = stack.pop();
for (Node next : curr.nexts) {
if (!set.contains(next)) {
// 遍历到没有访问过的邻居,打印该邻居
System.out.println(next.value);
// 记录该邻居已经访问过
set.add(next);
// 当前节点和邻居节点入栈,返回,进入下一轮循环
stack.push(curr);
stack.push(next);
break;
}
}
}
}
}
拓扑排序
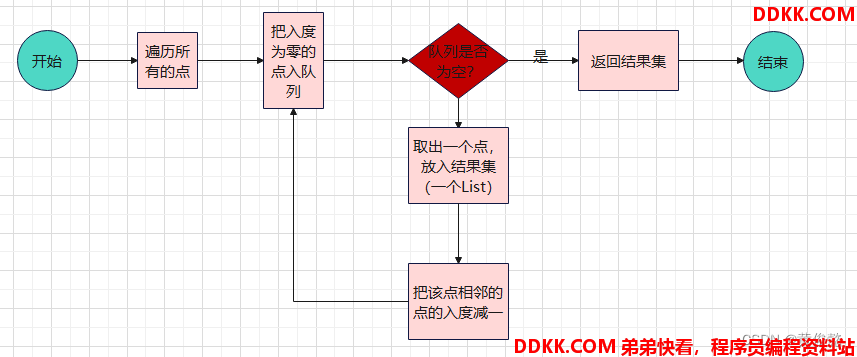
/**
* 拓扑排序
* 拓扑排序的图是有向无环图图
* Created by huangjunyi on 2022/8/30.
*/
public class Graph04 {
public static List<Node> sort(Graph graph) {
// 入度表 节点=>剩余入度
Map<Node, Integer> inMap = new HashMap<>();
// 剩余入度为0的节点,会入这个队列
Queue<Node> zeroInQueue = new LinkedList<>();
// 初始化zeroInQueue,入度为0的点入队列
for (Node node : graph.nodes.values()) {
inMap.put(node, node.in);
if (node.in == 0) {
zeroInQueue.offer(node);
}
}
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
// 弹出zeroInQueue的一个节点,放入结果
Node curr = zeroInQueue.poll();
result.add(curr);
// 把当前节点的邻居节点的入度-1
for (Node next : curr.nexts) {
inMap.put(next, inMap.get(next) - 1);
// 如果节点入度减到0,入队列
if (inMap.get(next) == 0) {
zeroInQueue.offer(next);
}
}
}
return result;
}
}
利用kruskal算法生成最小生成树
kruskal算法是在无向图中求最小生成树的算法
最小生成树:在不破坏连通性的情况下,返回图中权重最小边的集合
1、 所有边根据权重从小到大排序;
2、 按顺序遍历每条边,没有形成环,就选这条边;
检查是否形成环:
1、 使用并查集,一条边的两个节点不在一个集合中的,则可以选;
2、 选了之后该边的两个节点所在的集合就要合并;
/**
* 最小生成树
* 在不破坏连通性的情况下,返回图中权重最小边的集合
* 利用kruskal算法生成最小生成树
* Created by huangjunyi on 2022/8/30.
*/
public class Graph05 {
static class UnionSet<T> {
/**
* 存放子Node到父Node的映射
*/
private Map<Node, Node> parentMap = new HashMap<>();
/**
* 存放根Node与集合大小的映射
*/
private Map<Node, Integer> sizeMap = new HashMap<>();
public UnionSet(Collection<Node> values) {
for (Node node : values) {
parentMap.put(node, node);
sizeMap.put(node, 1);
}
}
public Node findRootNode(Node node) {
Stack<Node> stack = new Stack<>();
//一直往上寻找,找到找到根Node,沿途的Node记录到stack
while (parentMap.get(node) != node) {
stack.push(node);
node = parentMap.get(node);
}
//修改沿途的Node的父节点,使得下次findRootNode的代价更小
while (!stack.isEmpty()) parentMap.put(stack.pop(), node);
return node;
}
public boolean isSameSet(Node a, Node b) {
//a对应的Node,和b对应的Node,同时找到根Node,如果是同一个根Node,代表a和b在一个集合中
return findRootNode(a) == findRootNode(b);
}
public void union(Node a, Node b) {
//a对应的Node,和b对应的Node,同时往上找到根Node
Node rootNodeA = findRootNode(a);
Node rootNodeB = findRootNode(b);
//在同一个集合中,不用合并
if (rootNodeA == rootNodeB) return;
int sizeA = sizeMap.get(rootNodeA);
int sizeB = sizeMap.get(rootNodeB);
//数量小的集合的根Node的父Node指向数量大的集合的跟Node
//然后更新sizeMap信息,sizeMap只需要存储根Node与集合大小的映射
if (sizeA <= sizeB) {
parentMap.put(rootNodeA, rootNodeB);
sizeMap.put(rootNodeB, sizeA + sizeB);
sizeMap.remove(rootNodeA);
} else {
parentMap.put(rootNodeB, rootNodeA);
sizeMap.put(rootNodeA, sizeA + sizeB);
sizeMap.remove(rootNodeB);
}
}
public int countSet() {
return sizeMap.size();
}
}
public static Set<Edge> kruskalMST(Graph graph) {
//根据图中的点构建一个并查集
UnionSet unionSet = new UnionSet(graph.nodes.values());
//对所有的边进行排序,权重小的牌前面
PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.value));
queue.addAll(graph.edges);
//每次从堆中取出一条边,如果两个点不在一个集合里面,保留这条边到结果集中,并把两个点在并查集中合并
Set<Edge> result = new HashSet<>();
while (!queue.isEmpty()) {
Edge e = queue.poll();
if (!unionSet.isSameSet(e.from, e.to)) {
result.add(e);
unionSet.union(e.from, e.to);
}
}
return result;
}
}
Prim算法求最小生成树
- 从一个点出发,取与该点相邻的权重最小的边,然后把边加到结果集中
- 然后取该边对端的点,继续取权重最小的边,放入结果集
- 访问过的点和边要记录下来,如果取出的权重最小的边已经被记录访问过,则丢弃
- 如果取出的边对端的点已经被访问过,该边也丢弃
- 周而复始,直到访问完所有的边
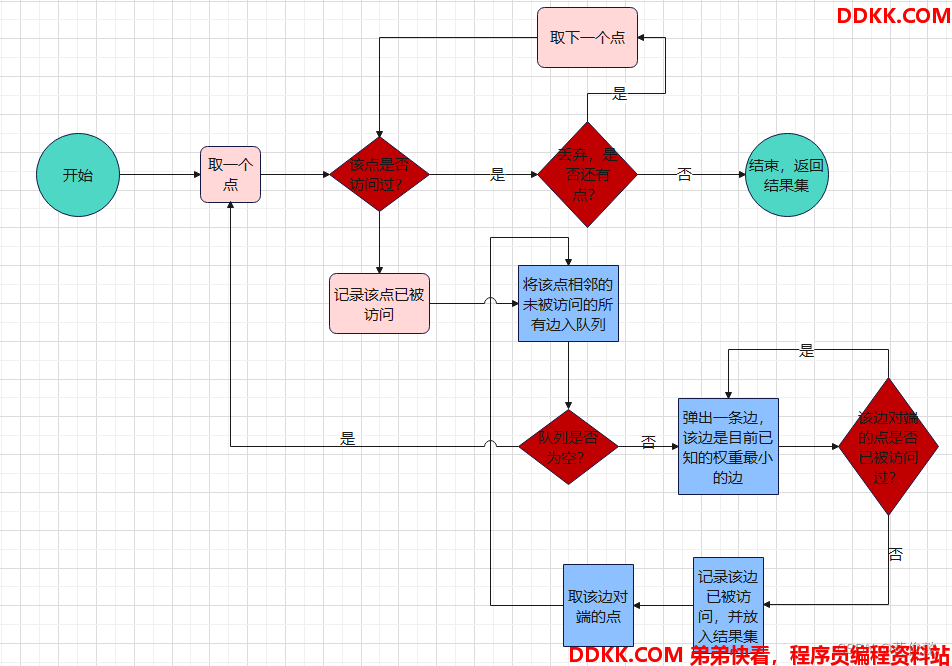
/**
* Prim算法求最小生成树
* 从一个点出发,取与该点相邻的权重最小的边,然后把边加到结果集中
* 然后取该边对端的点,继续取权重最小的边,放入结果集
* 访问过的点和边要记录下来,如果取出的权重最小的边已经被记录访问过,则丢弃
* 如果取出的边对端的点已经被访问过,该边也丢弃
* 周而复始,直到访问完所有的边
* Created by huangjunyi on 2022/8/31.
*/
public class Graph06 {
public static Set<Edge> primMST(Graph graph) {
// 记录访问过的节点
Set<Node> visitedNodes = new HashSet<>();
// 记录访问过的边
Set<Edge> visitedEdges = new HashSet<>();
// 最小生成树的边集
Set<Edge> result = new HashSet<>();
// 解锁了的边会放到小根堆中,按权重从小到大排序
PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.value));
//图有可能是森林(多个互相不连通的图),所以通过for循环遍历
for (Node node : graph.nodes.values()) {
if (!visitedNodes.contains(node)) {
// 如果一个节点没有访问过,访问,并看看边是否没有访问过,如果没有访问过,解锁
visitedNodes.add(node);
for (Edge edge : node.edges) {
if (!visitedEdges.contains(edge)) {
visitedEdges.add(edge);
queue.offer(edge);
}
}
// 遍历,直到小根堆为空,这一个子图就遍历完了
while (!queue.isEmpty()) {
// 小根堆弹出已解锁的权值最小的边
Edge currEdge = queue.poll();
// 访问to节点
Node toNode = currEdge.to;
// 如果to节点没有访问过,访问,并看看边是否没有访问过,如果没有访问过,解锁
if (!visitedNodes.contains(toNode)) {
visitedNodes.add(toNode);
result.add(currEdge);
for (Edge edge : toNode.edges) {
if (!visitedEdges.contains(edge)) {
visitedEdges.add(edge);
queue.offer(edge);
}
}
}
}
}
}
return result;
}
}
Dijkstra算法求一个起始点到所有点的最短距离
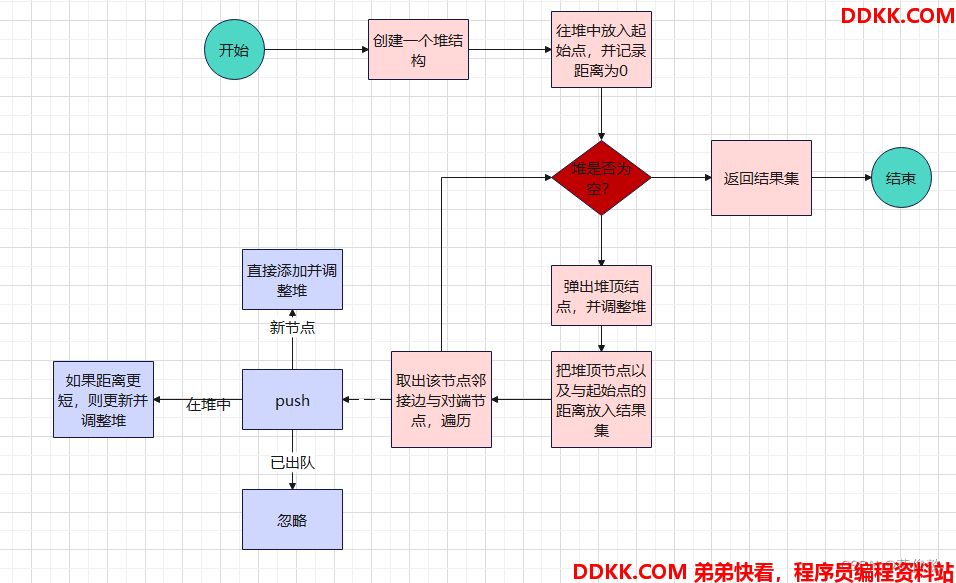
Dijkstra算法用于在有向无负权重的图(可以有环)中,算出某一个节点到图中所有节点的距离,返回一张距离表
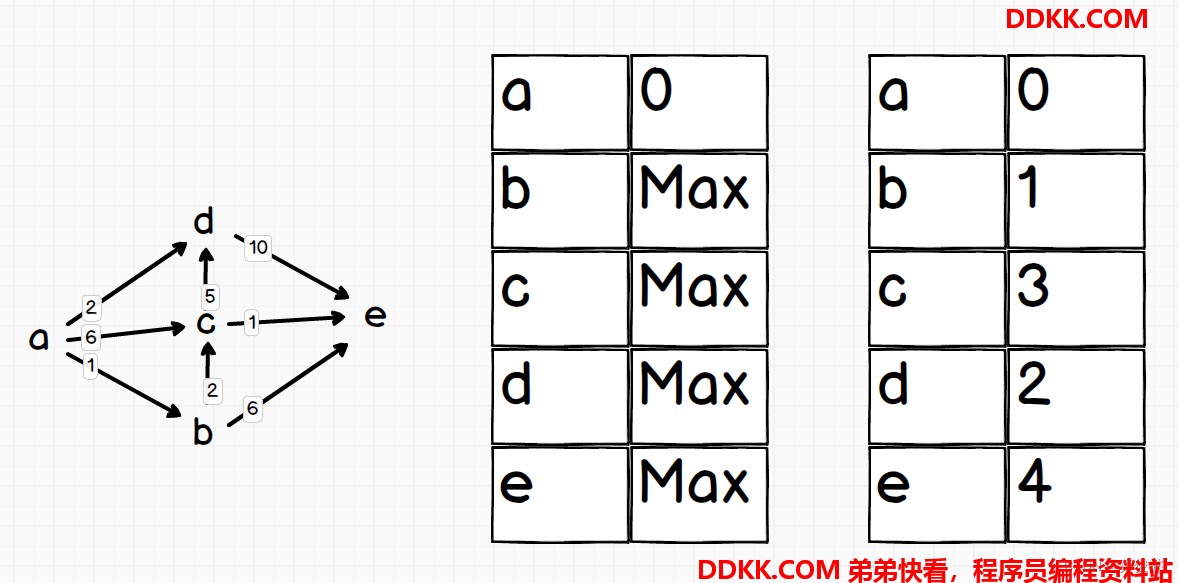
1、 定义一个堆,并且该堆可以调整元素的value(到原点的距离),然后重写排序;
2、 一开始先放入原点到堆中,并且距离是0;
3、 循环判断堆是否为空,不为空则弹出一个节点并进行堆调整,此时该节点到原点的距离就是最短距离,放入结果集中;
4、 取出该点的所有邻接点,遍历所有邻接点,并判断邻接点是否未进入过堆,是则直接放入堆中然后进行堆调整;如果该节点在堆中但是未弹出,则判断当前算出的距离(当前弹出的node与原点的距离+该邻接点与当前弹出结点间的边的权重)是否更小,是则更新该节点在堆中记录的value(与原点的距离)并进行堆调整;如果以上两个条件不满足,表示该节点曾经进入过堆并且已经弹出,忽略该节点;
5、 直到堆为空,退出循环;
/**
* Dijkstra算法求一个起始点到所有点的最短距离
* Created by huangjunyi on 2022/8/31.
*/
public class Graph07 {
private static class NodeHeap {
private Node[] heap;
private Map<Node, Integer> distanceMap;
private Map<Node, Integer> indexMap;
private int size;
public NodeHeap(int size) {
this.size = size;
this.heap = new Node[size];
this.distanceMap = new HashMap<>();
this.indexMap = new HashMap<>();
}
/**
* 往堆中放入节点,如果存在则更新,如果已经已经出队则忽略
* @param node
* @param distance
*/
public void push(Node node, int distance) {
if (!indexMap.containsKey(node)) {
//如果indexMap中的key不包含该node,则表示该node从未进过堆,直接添加
heap[size] = node;
distanceMap.put(node, distance);
indexMap.put(node, size);
floatUp(size++);
} else if (indexMap.get(node) != -1 && distance < distanceMap.get(node)) {
//如果indexMap中的key包含该node,且value不等于-1,则表示该node在堆中未弹出
//如果该node与起始点新的距离比distanceMap中记录的小,则更新distanceMap同时进行堆调整
distanceMap.put(node, distance);
floatUp(indexMap.get(node));
}
}
/**
* 弹出堆顶节点,返回其与起始点的最小距离
* @return
*/
public PopNode pop() {
PopNode popNode = new PopNode(heap[0], distanceMap.get(heap[0]));
distanceMap.remove(heap[0]);
indexMap.put(heap[0], -1);
swap(0, size - 1);
heap[--size] = null;
sink(0);
return popNode;
}
/**
* 堆向下调整
* @param i
*/
private void sink(int i) {
int left = i * 2 + 1;
while (left < size) {
int smallChild = distanceMap.get(heap[left]) < distanceMap.get(heap[left + 1]) ? left : left + 1;
if (distanceMap.get(heap[smallChild]) < distanceMap.get(heap[i])) {
swap(smallChild, i);
i = smallChild;
left = i * 2 + 1;
} else {
break;
}
}
}
/**
* 堆向上调整
* @param i
*/
private void floatUp(int i) {
while (i > 0) {
if (distanceMap.get(heap[i]) < distanceMap.get(heap[(i - 1) / 2])) {
swap(i, (i - 1) / 2);
i = (i - 1) / 2;
} else {
break;
}
}
}
private void swap(int i, int j) {
indexMap.put(heap[i], j);
indexMap.put(heap[j], i);
Node temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
public boolean isEmpty() {
return size == 0;
}
}
private static class PopNode {
private Node node;
private int distance;
public PopNode(Node node, int distance) {
this.node = node;
this.distance = distance;
}
}
public static Map<Node, Integer> dijkstra(Node head, int size) {
//创建一个堆结构
NodeHeap nodeHeap = new NodeHeap(size);
/**
* push方法三种处理:
* 1、如果该节点未进入过堆,则直接添加,并进行堆调整
* 2、如果该节点进入过堆,但是未弹出,如果与起始点新的距离更短,则更新距离并调整堆
* 3、如果该节点进入过堆,但是已经弹出,直接忽略
*/
nodeHeap.push(head, 0);
Map<Node, Integer> result = new HashMap<>();
//循环直到堆为空
while (!nodeHeap.isEmpty()) {
//弹出的就是最终该节点与起始点的最短距离
PopNode popNode = nodeHeap.pop();
result.put(popNode.node, popNode.distance);
//遍历该节点的邻接边,调用push方法尝试放入或更新对端的点
for (Edge edge : popNode.node.edges) {
nodeHeap.push(edge.to, popNode.distance + edge.value);
}
}
return result;
}
}
附加-Dinic算法解决最大网络流问题
给定一个有向图,边代表水管,而边的权重代表水管最大的承载水量
然后再给定图中的一个出发点和目标点
问从出发点到目标点的最大灌水量
比如,这样一副有向图,出发点是a,目标点是d,最大灌水量就是100+30=130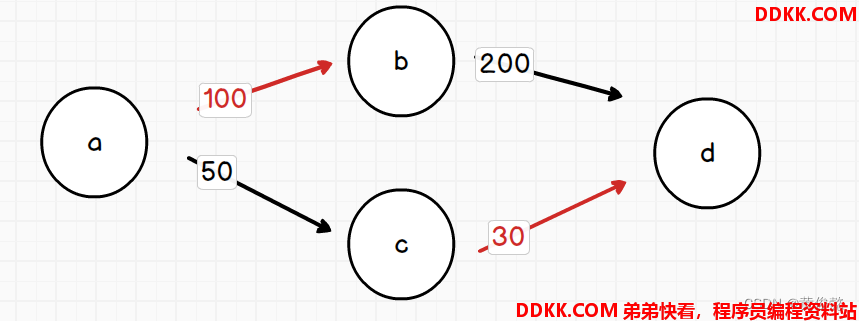
红色的水管就是瓶颈
解法一:深度优先遍历取每条路线的最小值,然后走过的路都减去流过的水量,最后累加每条路线得出的最小值?
看似可以,但是会得到错误解
比如
这样一副有向图,出发点是a,目标点是d
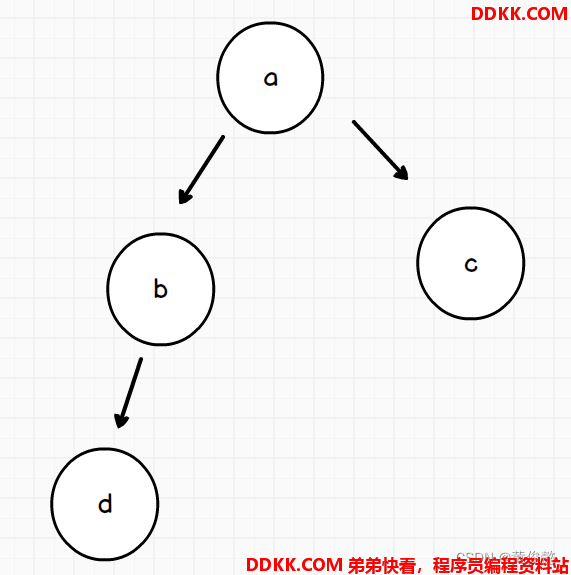
如果第一次深度优先遍历,走的路线是这样
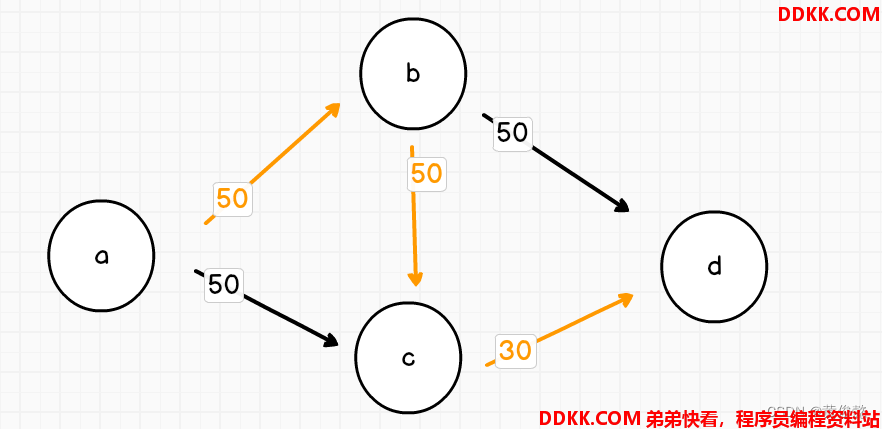
然后得出该路线最小值是50,然后沿途都扣减50
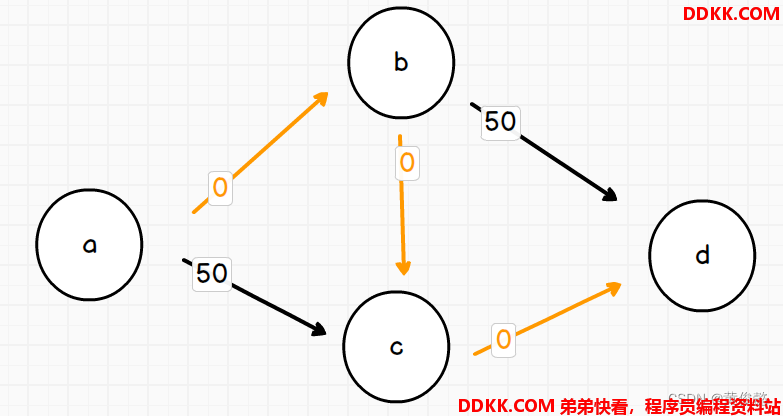
此时发现无路可走了,返回了一个错误答案50
那么,在走过的路上,补一条反向边,反向边权重就是正向边扣减调的承载水量
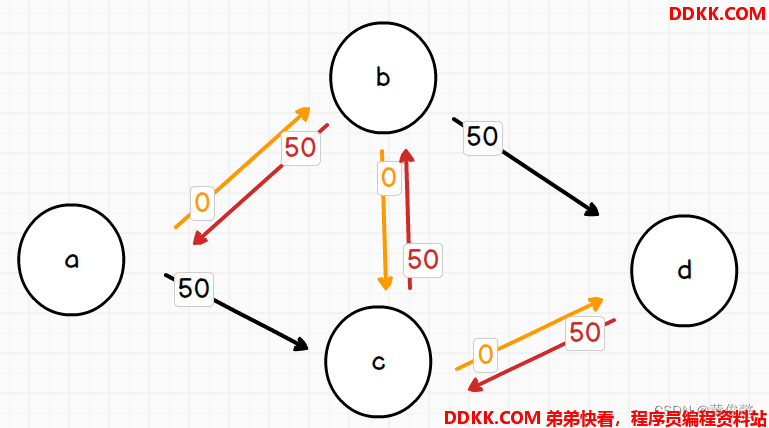
那么就不会因为路线选的不好,导致无路可走的情况
第二次遍历的时候,a到d还是有路可走的,并且最后得出正确答案
这就是Dinic算法的其中一个优化
Dinic算法第二个优化,建立高度
宽度优先遍历,得到高度信息 a高度为0,b/c高度为1,d的高度为2,有一个数组记录[0,1,1,2]
这样就可以优化深度优先遍历的常数时间,相同层的路径不要走,这样就规避了b到c的路径
还有一个优化,就是解决这种情况:
一条路径走过一个点,流经某个点,而这个点又流经某些边,去往下一个点
拿这条路径返回到上层节点,继续往下尝试其他的支路,又走到了这个点,那么之前走过的边,如果载水量耗尽,是不能再走的,因此每次都要判断一下载水量再走
那为了优化这种判断,搞一个cur数组,cur[s]表示s这个点,从cur[s]这条边开始,cur[s]往下的都是别的支路占用的,不能再走了
代码:
/**
* Dinic算法解决最大网络流问题
* Created by huangjunyi on 2022/12/11.
*/
public class _18DinicAlgorithm {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
int cases = (int) in.nval;
for (int i = 1; i <= cases; i++) {
in.nextToken();
int n = (int) in.nval;
in.nextToken();
int s = (int) in.nval;
in.nextToken();
int t = (int) in.nval;
in.nextToken();
int m = (int) in.nval;
Dinic dinic = new Dinic(n);
for (int j = 0; j < m; j++) {
in.nextToken();
int from = (int) in.nval;
in.nextToken();
int to = (int) in.nval;
in.nextToken();
int weight = (int) in.nval;
dinic.addEdge(from, to, weight);
dinic.addEdge(to, from, weight);
}
int ans = dinic.maxFlow(s, t);
out.println("Case " + i + ": " + ans);
out.flush();
}
}
}
/**
* 边
*/
public static class Edge {
public int from; // 从哪
public int to; // 到哪
public int available; // 权重(承载水量)
public Edge(int a, int b, int c) {
from = a;
to = b;
available = c;
}
}
public static class Dinic {
private int N; // 边数
private ArrayList<ArrayList<Integer>> nexts; // 城市编号 => [能走的边的边号]
private ArrayList<Edge> edges; // 边号 => 边
private int[] depth; // 高度数组
private int[] cur; // cur数组,边号 => 从哪条边开始尝试,比如cur[s]=2,表示s这个点还能走nexts.get(s)中大于等于2的边,小于的是别的支路走过的,不能重复往里灌水
public Dinic(int nums) {
N = nums + 1;
nexts = new ArrayList<>();
for (int i = 0; i <= N; i++) {
nexts.add(new ArrayList<>());
}
edges = new ArrayList<>();
depth = new int[N];
cur = new int[N];
}
public void addEdge(int u, int v, int r) {
int m = edges.size();
// 加正向边
edges.add(new Edge(u, v, r));
nexts.get(u).add(m);
// 加反向边
edges.add(new Edge(v, u, 0));
nexts.get(v).add(m + 1);
}
/**
* 算法主流程
* @param s 起始点
* @param t 目标点
* @return 最大灌水量
*/
public int maxFlow(int s, int t) {
int flow = 0;
while (bfs(s, t)) {
// s -> t,还有路能走?
Arrays.fill(cur, 0); // 还原cur数组
flow += dfs(s, t, Integer.MAX_VALUE); // 走 =>
Arrays.fill(depth, 0); // 还原高度数组
}
return flow;
}
/**
* 宽度优先遍历,建立高度数组
*/
private boolean bfs(int s, int t) {
LinkedList<Integer> queue = new LinkedList<>();
queue.addFirst(s);
boolean[] visited = new boolean[N];
visited[s] = true;
while (!queue.isEmpty()) {
int u = queue.pollLast();
for (int i = 0; i < nexts.get(u).size(); i++) {
Edge e = edges.get(nexts.get(u).get(i));
int v = e.to;
if (!visited[v] && e.available > 0) {
visited[v] = true;
// 子节点高度 = 父节点高度 + 1
depth[v] = depth[u] + 1;
if (v == t) {
break;
}
queue.addFirst(v);
}
}
}
return visited[t];
}
/**
* 当前来到了s点,s为可变参数,最终目标是t,t固定参数,r收到的任务
* 收集到的流,作为结果返回,ans <= r
* @param s 当前来到了s点
* @param t 最终目标是t
* @param r 收到的任务
* @return 收集到的流
*/
private int dfs(int s, int t, int r) {
if (s == t || r == 0) {
return r;
}
int f = 0;
int flow = 0;
// s点从哪条边开始试 -> cur[s]
for (; cur[s] < nexts.get(s).size(); cur[s]++) {
// cur[s]++,别的支路也走到当前节点,就接着往下尝试
int ei = nexts.get(s).get(cur[s]);
Edge e = edges.get(ei); // 正向边
Edge o = edges.get(ei ^ 1); // 方向边
if (depth[e.to] == depth[s] + 1 // 高度更大的才走
&& (f = dfs(e.to, t, Math.min(e.available, r))) != 0) {
e.available -= f; // 正向边扣减
o.available += f; // 反向边增加
flow += f; // 收集流
r -= f; // 要完成的任务扣减
if (r <= 0) {
// 任务都完成了,返回
break;
}
}
}
return flow;
}
}
}