不使用递归,实现二叉树的前序、中序、后续遍历
前序:
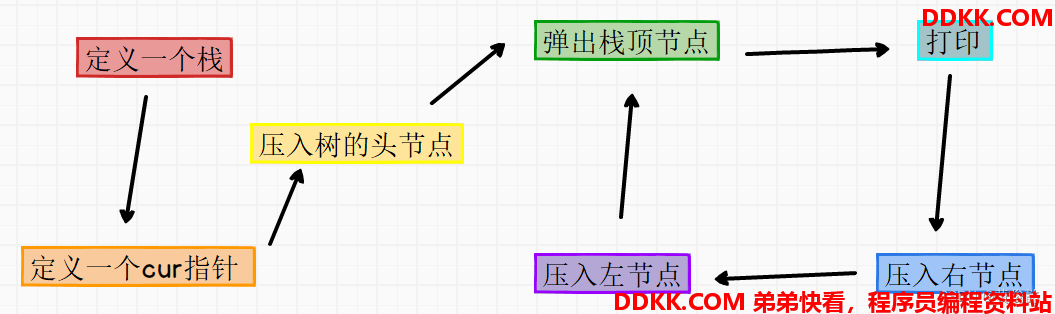
1、 定义一个栈结构;
2、 定义一个cur指针,接收从栈中弹出的节点;
3、 弹出栈顶节点打印,先压入右节点,再压入左节点;
后序:
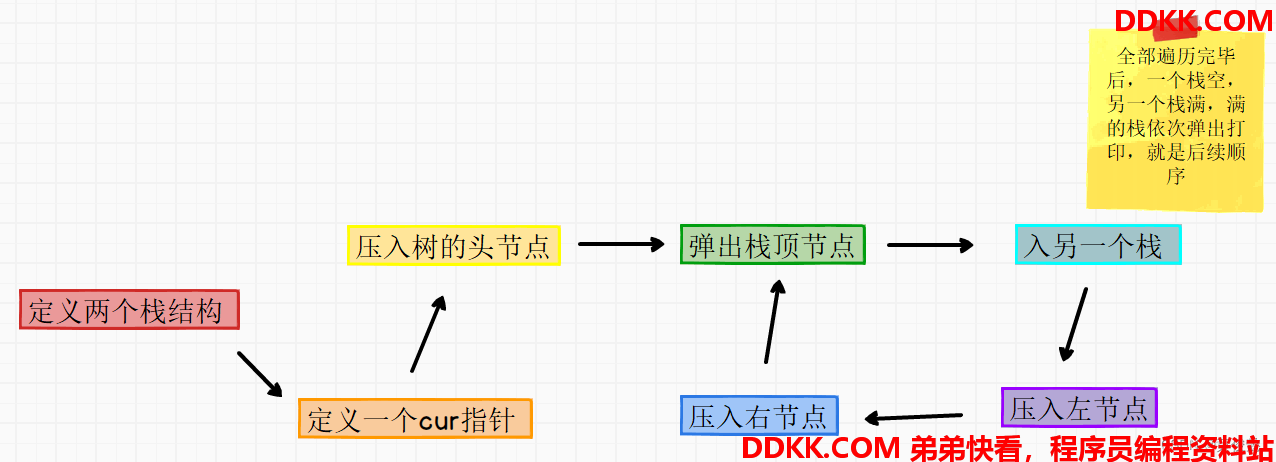
1、 定义两个栈结构;
2、 定义一个cur指针,接收从栈中弹出的节点;
3、 弹出栈顶节点入另一个栈,先压入左节点,再压入右节点;
4、 全部遍历完毕后,一个栈空,另一个栈满,满的栈依次弹出打印,就是后续顺序;
中序:
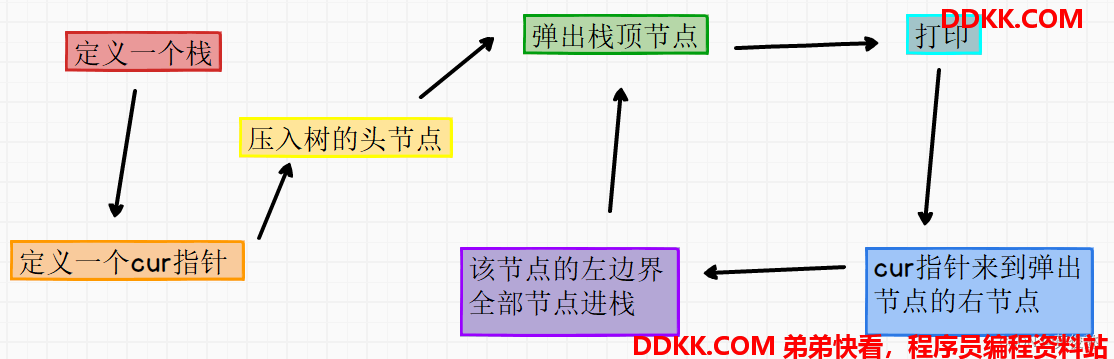
1、 定义一个栈结构;
2、 每遍历到一个节点,先把左边界全部进栈;
3、 弹出一个节点打印,然后cur指针来到弹出节点的右节点,继续把该节点的左边界全部节点进栈,周而复始;
/**
* 不使用递归,实现二叉树的前序、中序、后续遍历
*/
public class Tree01 {
/**
* 二叉树非递归前序遍历
* 1、用一个栈存放遍历到的结点
* 2、每次弹出栈顶元素,并且弹出就打印
* 3、如果有右结点,先压入右节点
* 4、如果有左结点,再压入左结点
* @param head
*/
public static void pre(Node head) {
if (head == null) return;
Stack<Node> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()) {
Node pop = stack.pop(); //弹出就打印
System.out.println(pop.value);
if (pop.right != null) stack.push(pop.right); //先压入右
if (pop.left != null) stack.push(pop.left); //再压入左
}
}
/**
* 二叉树非递归中序遍历
* 1、用一个栈存放遍历到的结点
* 2、先递归左子树,压入沿途经过的结点
* 3、左子树遍历完,弹出栈顶元素打印
* 4、取弹出结点的右结点,回到一,继续往左深度遍历
* @param head
*/
public static void in(Node head) {
if (head == null) return;
Stack<Node> stack = new Stack<>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
//深度遍历左子树
stack.push(head);
head = head.left;
} else {
//左子树遍历完,弹出栈顶元素打印
Node pop = stack.pop();
System.out.println(pop.value);
//取弹出元素的右结点,继续下一轮遍历
head = pop.right;
}
}
}
/**
* 二叉树非递归实现后续遍历
* 1、两个栈
* 2、先压入头结点到栈1,然后遍历
* 3、遍历过程中弹出栈顶元素,压入栈2
* 4、从栈1弹出的元素,先压入它的左节点到栈1,再压入右结点到栈1
* 5、下一轮遍历
*
* 6、上面遍历完后,栈1为空,此时栈2从栈顶到栈底结点顺序就是二叉树后续遍历的顺序,循环弹出栈2元素打印
* @param head
*/
public static void post01(Node head) {
if (head == null) return;
Stack<Node> stack1 = new Stack<>();
Stack<Node> stack2 = new Stack<>();
stack1.add(head);
while (!stack1.isEmpty()) {
Node pop = stack1.pop();
stack2.push(pop); //从栈1弹出栈顶元素,压入栈2
if (pop.left != null) stack1.push(pop.left); //先压入左到栈1
if (pop.right != null) stack1.push(pop.right); //再压入右到栈1
}
while (!stack2.isEmpty()) System.out.println(stack2.pop().value);
}
/**
* 二叉树非递归后续遍历:
* 1、用head指针记录上次处理过的结点
* 2、一颗子树中,先处理左结点,处理完拿head指针记一下
* 3、下次遍历通过head指针知道左结点已经处理,处理右节点,处理完head指针记一下
* 4、最后打印子树的头节点,并且head指针记一下,这颗子树就处理完
* @param head
*/
public static void post02(Node head) {
if (head == null) return;
Stack<Node> stack = new Stack<>();
stack.push(head);
Node help = null;
while (!stack.isEmpty()) {
help = stack.peek();
//左子树没有处理过,处理左子树
if (help.left != null && help.left != head && help.right != head) stack.push(help.left);
//右字树没有处理过,处理右子树
else if (help.right != null && help.right != head) stack.push(help.right);
else {
System.out.println(help.value); //左子树和右子树都处理完,打印help结点
head = help; //head赋值为help,代表上次遍历打印过的结点
}
}
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}
二叉树按层遍历,并且统计最大层的结点数
1、 二叉树按层遍历:定义一个队列,每次弹出一个节点时,把左右子节点依次入队列,即实现了按层遍历;
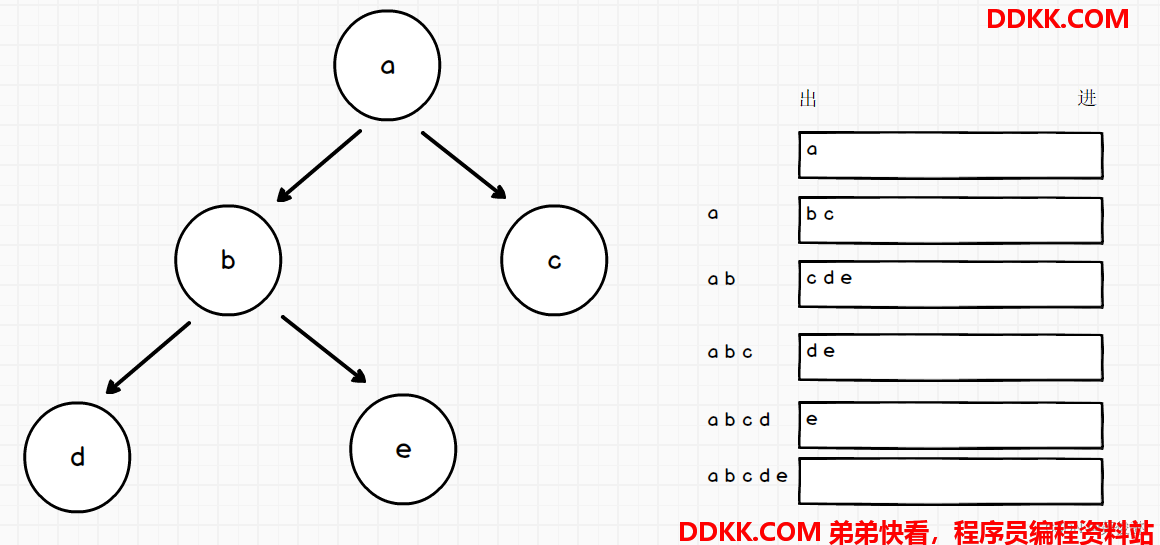
2、 每次遍历时,更新下一层最右节点,用一个变量记住;
3、 当遇到当前层最右节点时,结算当前层节点数;
/**
* 二叉树按层遍历,并且统计最大层的结点数
*/
public class Tree02 {
/**
* 用一个HashMap记录每个结点处于哪一层
* @param head
* @return
*/
public static int maxLevelNumber01(Node head) {
if (head == null) return 0;
Map<Node, Integer> nodeLevelMap = new HashMap<>();
nodeLevelMap.put(head, 1); //记录头结点为第一层
Queue<Node> queue = new LinkedList<>();
queue.offer(head);
int max = 0;
int currentLevel = 1; //当前正在遍历的层级
int currentLevelWidth = 0; //当前遍历层级的宽度
while (!queue.isEmpty()) {
Node node = queue.poll();
Integer nodeLevel = nodeLevelMap.get(node);
if (node.left != null) {
nodeLevelMap.put(node.left, nodeLevel + 1); //左结点层级为当前节点层级+1
queue.offer(node.left);
}
if (node.right != null) {
nodeLevelMap.put(node.right, nodeLevel + 1); //右结点层级为当前节点层级+1
queue.offer(node.right);
}
if (currentLevel == nodeLevel) currentLevelWidth++; //当前结点层级等于当前遍历层级,当前遍历层级宽度+1
else {
//当前结点层级不等于当前遍历层级,结算
max = Math.max(currentLevelWidth, max);
currentLevelWidth = 1;
currentLevel = nodeLevel;
}
}
max = Math.max(currentLevelWidth, max);
return max;
}
/**
* 用一个变量记录当前层的最右结点,当到达当前层最右结点时,结算
* @param head
* @return
*/
public static int maxLevelNumber02(Node head) {
if (head == null) return 0;
Queue<Node> queue = new LinkedList<>();
queue.offer(head);
Node currentLevelEnd = head; //当前遍历层的最右结点
Node nextLevelEnd = null; //下一层的最右结点
int max = 0; //最大层宽度
int currentLevelWidth = 0; //当前遍历层的宽度
while (!queue.isEmpty()) {
Node node = queue.poll();
currentLevelWidth++; //当前层宽度+1
if (node.left != null) {
queue.offer(node.left);
nextLevelEnd = node.left; //更新下一层的最右结点
}
if (node.right != null) {
queue.offer(node.right);
nextLevelEnd = node.right; //更新下一层的最右结点
}
//当前结点是当前层最右结点,结算
if (node == currentLevelEnd) {
max = Math.max(currentLevelWidth, max);
currentLevelWidth = 0;
currentLevelEnd = nextLevelEnd;
nextLevelEnd = null;
}
}
return max;
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}
按先序遍历方式,序列化和返序列化二叉树
序列化:
按先序的方式,递归把节点入队列,空节点也要放一个null
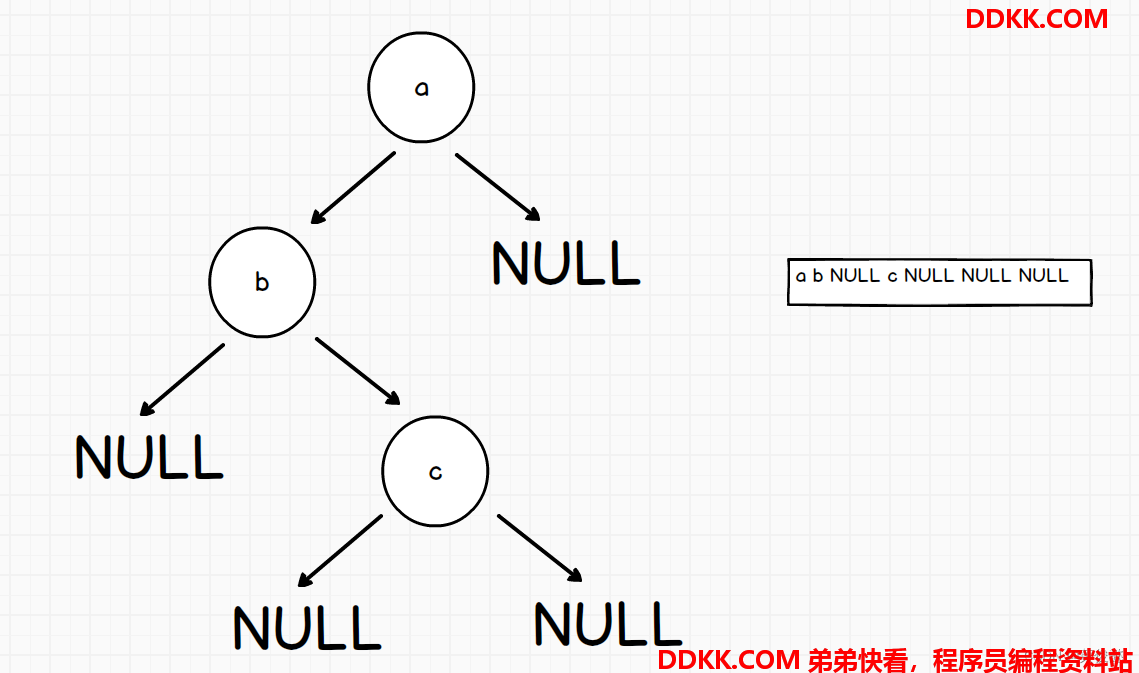
反序列化:
按先序的方式,递归从队列拿一个值,构建节点
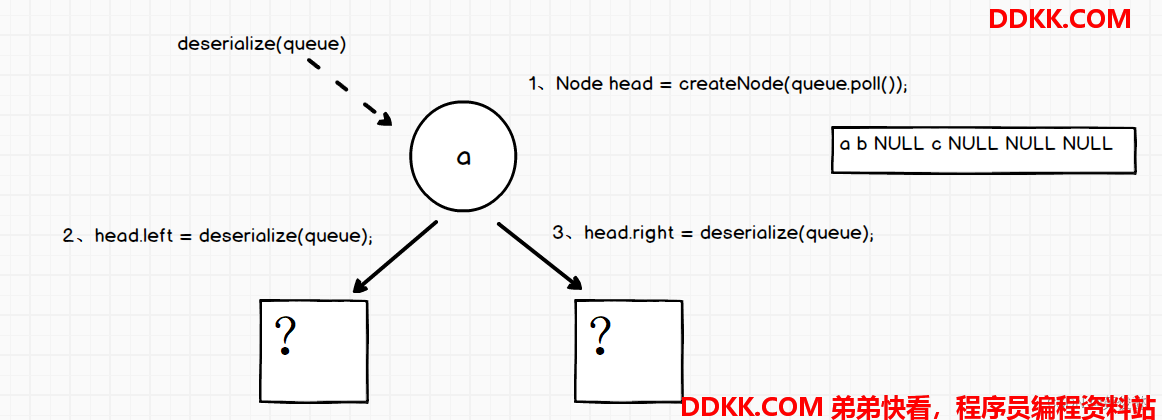
/**
* 按先序遍历方式,序列化和返序列化二叉树
*/
public class Tree03 {
public static Queue<Integer> serialize(Node head) {
Queue<Integer> queue = new LinkedList<>();
serialize(head, queue);
return queue;
}
private static void serialize(Node head, Queue<Integer> queue) {
if (head == null) queue.offer(null);
else {
//先序:先入序列化队列,再递归处理左右子结点
queue.offer(head.value);
serialize(head.left, queue);
serialize(head.right, queue);
}
}
public static Node deserialize(Queue<Integer> queue) {
if (queue == null || queue.isEmpty()) return null;
if (queue.peek() == null) {
queue.poll();
return null;
}
//先序:弹出的结点作为头结点,然后递归处理左右子结点
Node head = createNode(queue.poll());
head.left = deserialize(queue);
head.right = deserialize(queue);
return head;
}
private static Node createNode(int value) {
Node node = new Node();
node.value = value;
return node;
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}
中序是没有办法正确序列化和反序列化的,因为有歧义
向下面这种情况,同一个中序序列,可以对应不同结构的二叉树
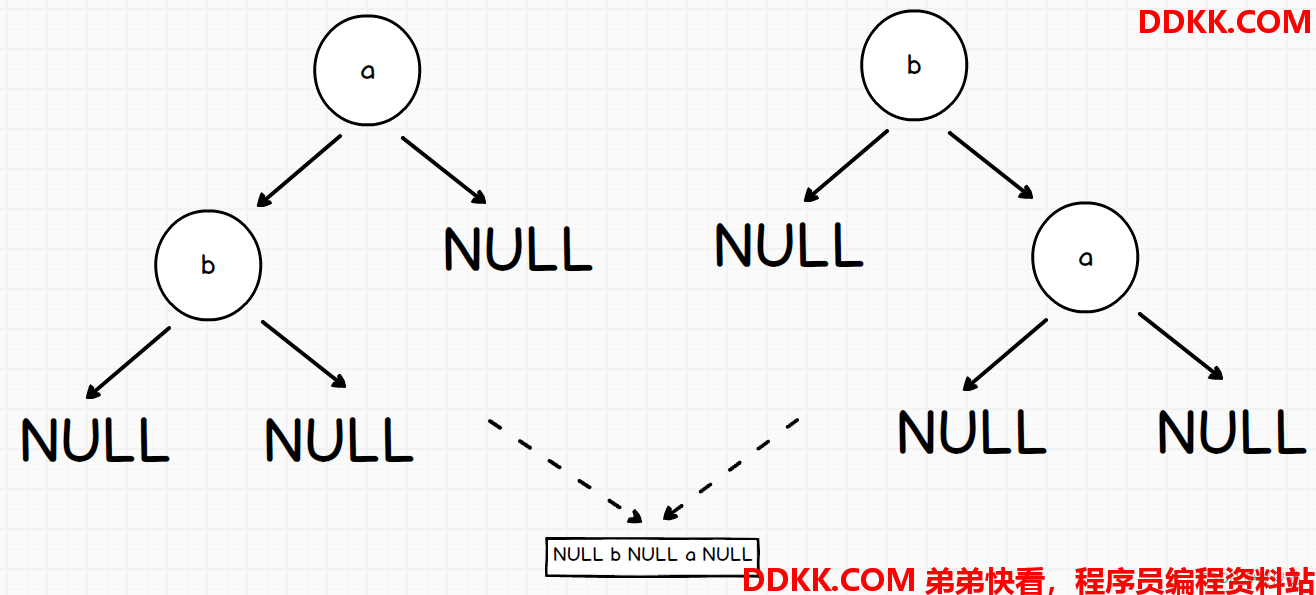
按层序列化和反序列化二叉树
序列化:
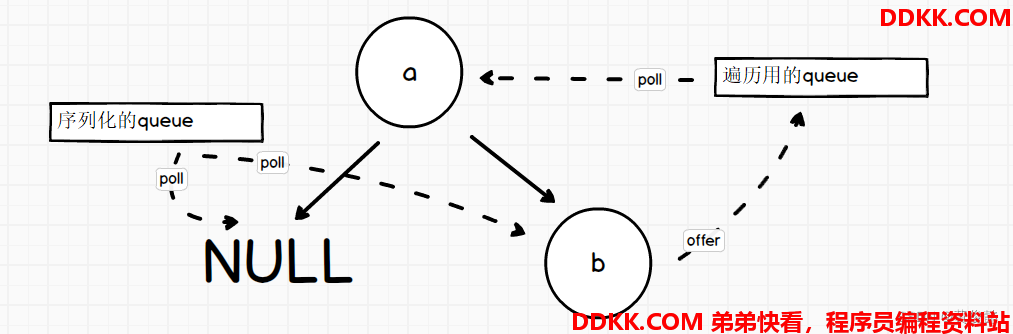
1、 声明一个队列,以按层遍历二叉树的方式,每个节点先序列化,再入队列;
2、 每次从队列中弹出一个节点,序列化它的左节点和右节点,然后把左节点和右节点入队列(null不入队列);
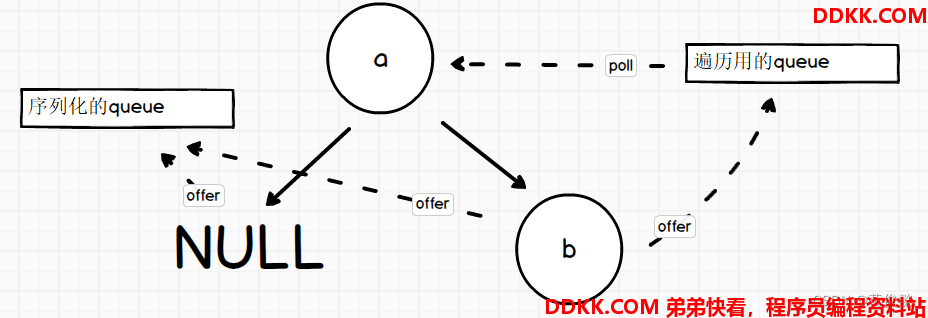
反序列化:
1、 声明一个队列,用于以中序的方式构建二叉树,先从序列化串中取出第一个值,构建头节点,放入队列中;
2、 每次弹出一个节点,从序列化取值,构建左右节点,再把左右节点入队列(null不入队列);
/**
* 按层序列化和反序列化二叉树
*/
public class Tree04 {
public static Queue<Integer> serialize(Node head) {
Queue<Integer> res = new LinkedList<>();
if (head == null) {
res.offer(null);
return res;
}
//先序列化,再入队列
Queue<Node> queue = new LinkedList<>();
res.offer(head.value);
queue.offer(head);
while (!queue.isEmpty()) {
Node node = queue.poll();
if (node.left == null) {
res.offer(null);
} else {
//结点不为空,序列化后如队列
res.offer(node.left.value);
queue.offer(node.left);
}
if (node.right == null) {
res.offer(null);
} else {
//结点不为空,序列化后如队列
res.offer(node.right.value);
queue.offer(node.right);
}
}
return res;
}
public static Node deserialize(Queue<Integer> queue) {
if (queue == null || queue.isEmpty()) return null;
Node head = createNode(queue.poll());
if (head != null) {
Queue<Node> queue1 = new LinkedList<>();
queue1.offer(head);
while (!queue1.isEmpty()) {
//从队列出队的结点,处理其左右子结点,然后左右子结点不为空的,入队列
Node node = queue1.poll();
node.left = createNode(queue.poll());
node.right = createNode(queue.poll());
if (node.left != null) queue1.offer(node.left);
if (node.right != null) queue1.offer(node.right);
}
}
return head;
}
private static Node createNode(Integer value) {
if (value == null) return null;
Node node = new Node();
node.value = value;
return node;
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}
实现多叉树和二叉树的互转
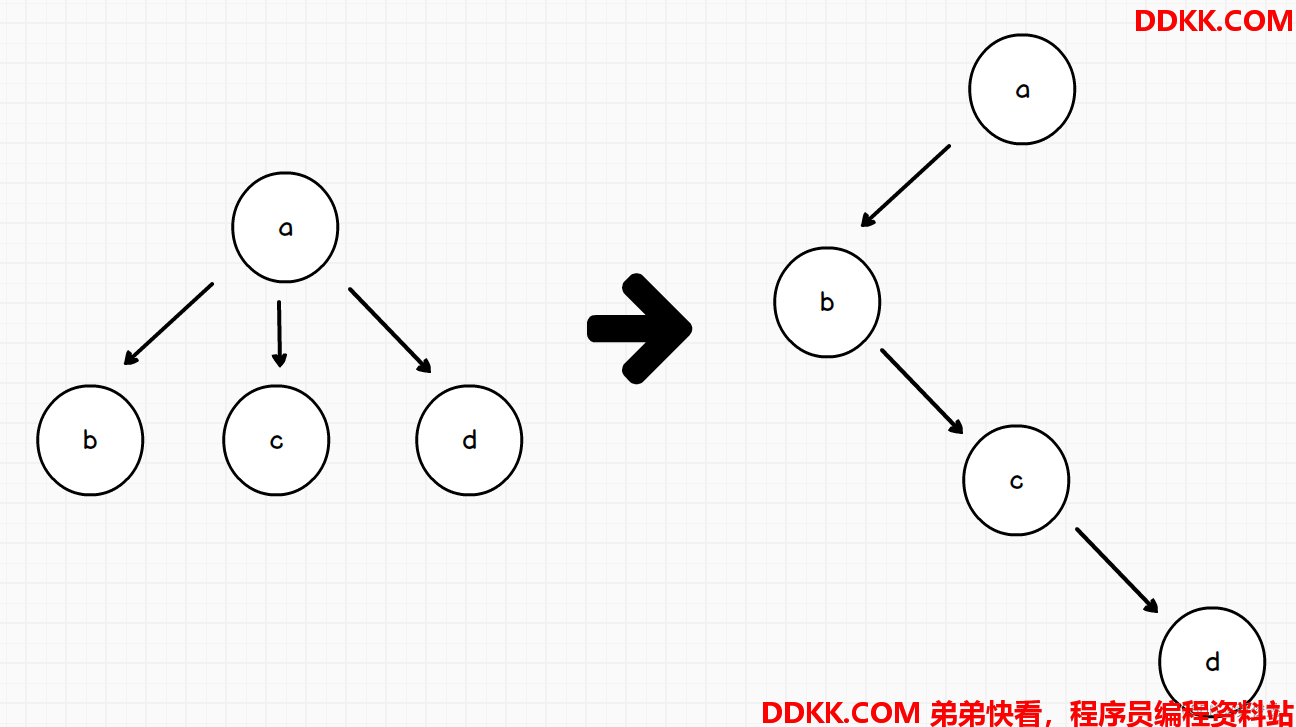
多叉树转二叉树:一个节点的所有子结点,转成二叉树后,变成该节点的左子结点以及左子节点的右节点链路
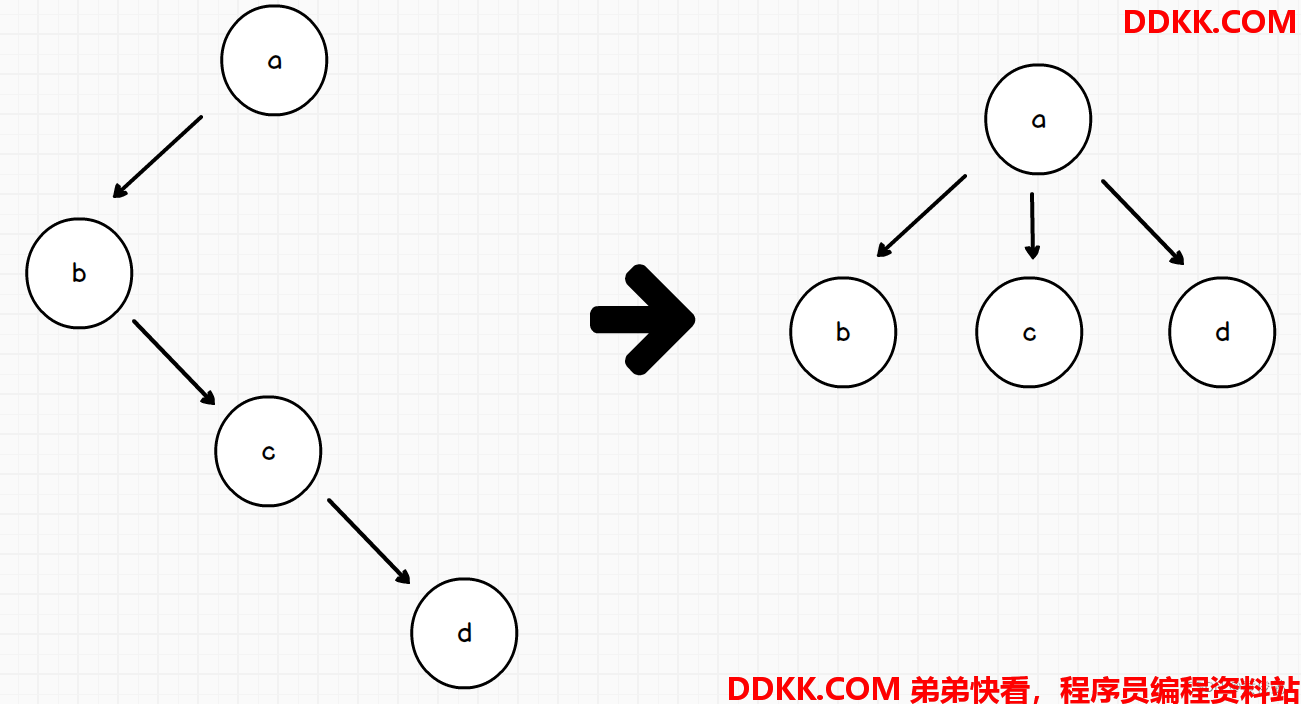
二叉树转多叉树:一个节点的左节点以及左节点的右节点链路,全部收集为该节点的子节点
/**
* 实现多叉树和二叉树的互转
* Created by huangjunyi on 2022/11/24.
*/
public class Tree09 {
private static class Node {
public int val;
public List<Node> children;
public Node() {
}
public Node(int val) {
this.val = val;
}
public Node(int val, List<Node> children) {
this.val = val;
this.children = children;
}
}
private static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) {
this.val = val;
}
}
class Codec {
/**
* 多叉树转二叉树
* @param root
* @return
*/
public TreeNode encode(Node root) {
if (root == null) return null;
// 二叉树头节点
TreeNode head = new TreeNode(root.val);
// 生成二叉树节点链表,挂到左节点上
head.left = nodeListToTreeNode(root.children);
return head;
}
/**
* 多叉树的子节点List转成二叉树的节点链表返回
* 多叉树的子节点的子节点List,会递归处理
* @param children
* @return
*/
private TreeNode nodeListToTreeNode(List<Node> children) {
TreeNode head = null;
TreeNode pre = null;
TreeNode cur = null;
for (Node child : children) {
// 封装成二叉树节点
cur = new TreeNode(child.val);
// 递归生成该二叉树节点的左节点上的节点链表
cur.left = nodeListToTreeNode(child.children);
if (head == null) head = cur;
if (pre != null) pre.right = cur;
pre = cur;
}
return head;
}
/**
* 二叉树转多叉树
* @param root
* @return
*/
public Node decode(TreeNode root) {
if (root == null) return null;
// 多叉树头节点,并且转换二叉树左节点上的节点链表为多叉树子节点List
return new Node(root.val, treeNodeToNodeList(root.left));
}
/**
* 二叉树的节点链表转成多叉树的子节点List
* @param root
* @return
*/
public List<Node> treeNodeToNodeList(TreeNode root) {
List<Node> children = new ArrayList<>();
TreeNode cur = root;
while (cur != null) {
// 封装为多叉树节点,递归转换当前二叉树节点的左节点上的节点链表为该多叉树节点的子节点List
Node node = new Node(cur.val, treeNodeToNodeList(cur.left));
// 收集多叉树节点到List
children.add(node);
cur = cur.right;
}
return children;
}
}
}
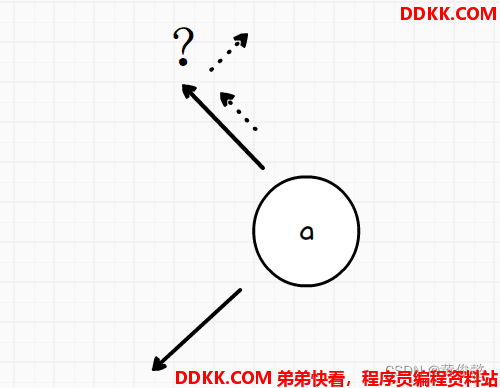
给定一个二叉树结点,有左右结点指针,也有父节点指针,找到它在中序遍历上的后继结点
有两种情况
1、 如果该节点有右树,那么后继节点就是右树上的最左节点;
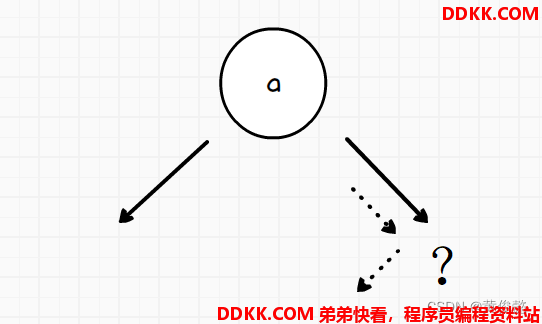
2、 如果该节点没有右树,那么往上找,直到找到某个节点是它父节点的左节点,那么后继节点就是这个父节点;
/**
* 给定一个二叉树结点,有左右结点指针,也有父节点指针,找到它在中序遍历上的后继结点
*/
public class Tree05 {
public static Node findSuccessorNode(Node node) {
if (node == null) return node;
if (node.right != null) {
//有右结点,找到右结点的最左结点
return findLeftMost(node.right);
} else {
//没有右结点,则往上找父节点,直到父节点的左结点引用指向的是当前结点所在的子树
Node parent = node.parent;
while (parent != null && parent.left != node) {
node = parent;
parent = node.parent;
}
return parent;
}
}
private static Node findLeftMost(Node node) {
while (node.left != null) node = node.left;
return node;
}
private static class Node {
private int value;
private Node left;
private Node right;
private Node parent;
}
}
纸条对折N次,然后打印折痕的方向
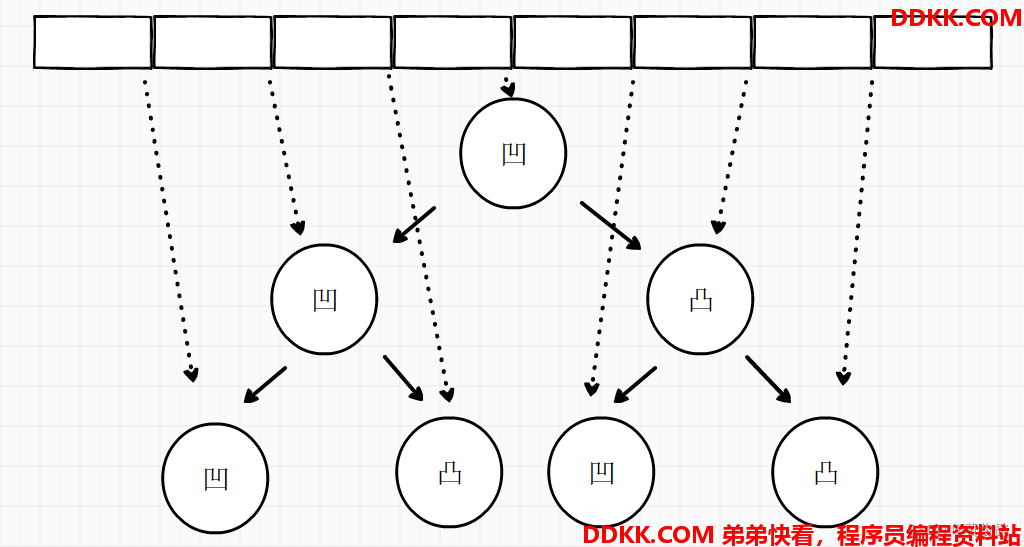
拿一张纸条,对折N次,然后从上往下,打印折痕的方向,折痕向下,打印down,折痕向上,打印up。
例如对折了3次的纸条:
/**
* 纸条对折N次,然后打印折痕的方向
* 拿一张纸条,对折N次,然后从上往下,打印折痕的方向
* 折痕向下,打印down,折痕向上,打印up
*/
public class Tree06 {
public static void print(int n) {
print(n, 1, true);
}
/**
* 二叉树中序遍历的方式打印折痕
* @param n 总共层数(对折次数)
* @param curr 当前层数
* @param down 是否是凹折痕
*/
private static void print(int n, int curr, boolean down) {
if (curr > n) return;
print(n, curr + 1, true);
System.out.println(down ? "down" : "up");
print(n, curr + 1, false);
}
}
给定一颗二叉树,判断其是否是完全二叉树
按层遍历二叉树,并进行判断:
1、 如果有某个结点有右节点但是没有左结点,则不是完全二叉树;
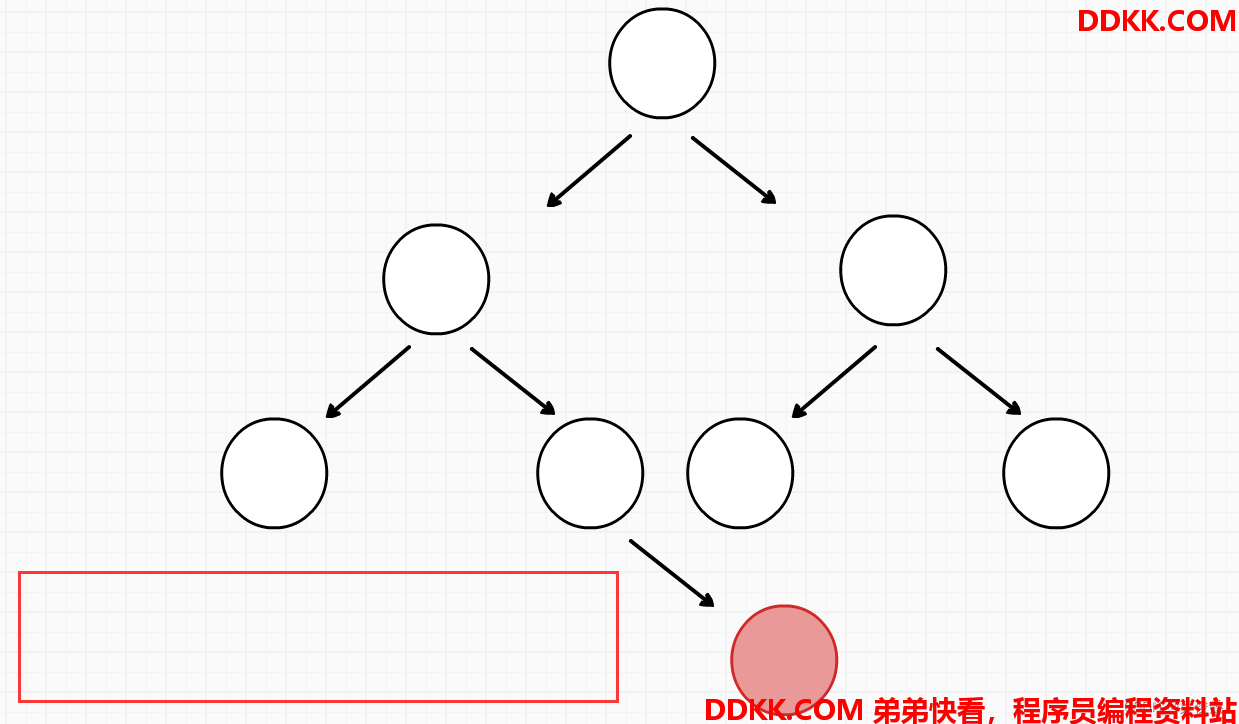
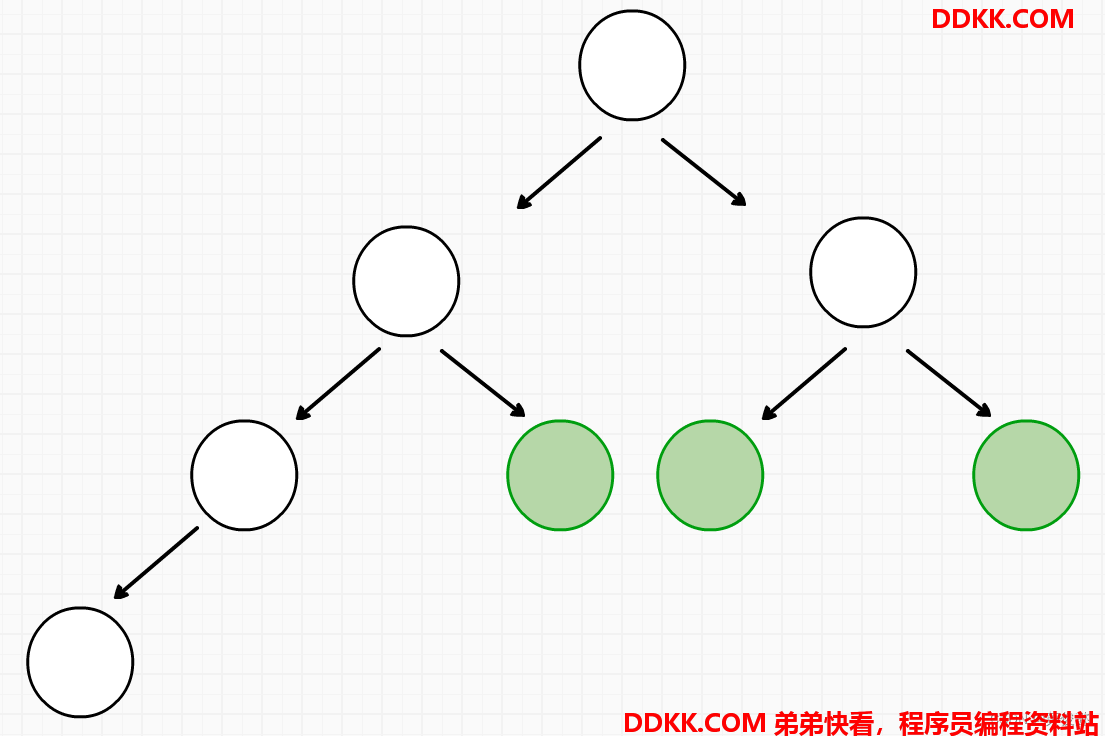
2、 如果遍历到某个结点不是同时拥有左右子结点,则后续遍历到的结点必须都是叶子结点,否则不是完全二叉树;
/**
* 给定一颗二叉树,判断其是否是完全二叉树
*
* 按层遍历二叉树,并进行判断:
* 1、如果有某个结点有右节点但是没有左结点,则不是完全二叉树
* 2、如果遍历到某个结点不是同时拥有左右子结点,则后续遍历到的结点必须都是叶子结点,否则不是完全二叉树
*/
public class Tree07 {
public static boolean isCBT(Node head) {
if (head == null) return true;
// 队列,按层遍历
Queue<Node> queue = new LinkedList<>();
queue.offer(head);
// 遇到了不同时拥有左右子节点时,改为true,后续所有的节点都必须是叶子节点
boolean leaf = false;
while (!queue.isEmpty()) {
Node node = queue.poll();
Node left = node.left;
Node right = node.right;
// 如果有右无左,一定不是完全二叉树,如果leaf为true,后续遇到了不是叶子节点的节点,一定不是完全二叉树
if ((left == null && right != null) || (leaf && (left != null || right != null))) {
return false;
}
// 按层遍历的操作
if (left != null) queue.offer(left);
if (right != null) queue.offer(right);
// 遇到了不同时拥有左右子节点时,改为true,后续所有的节点都必须是叶子节点
if (left == null || right == null) leaf = true;
}
return true;
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}
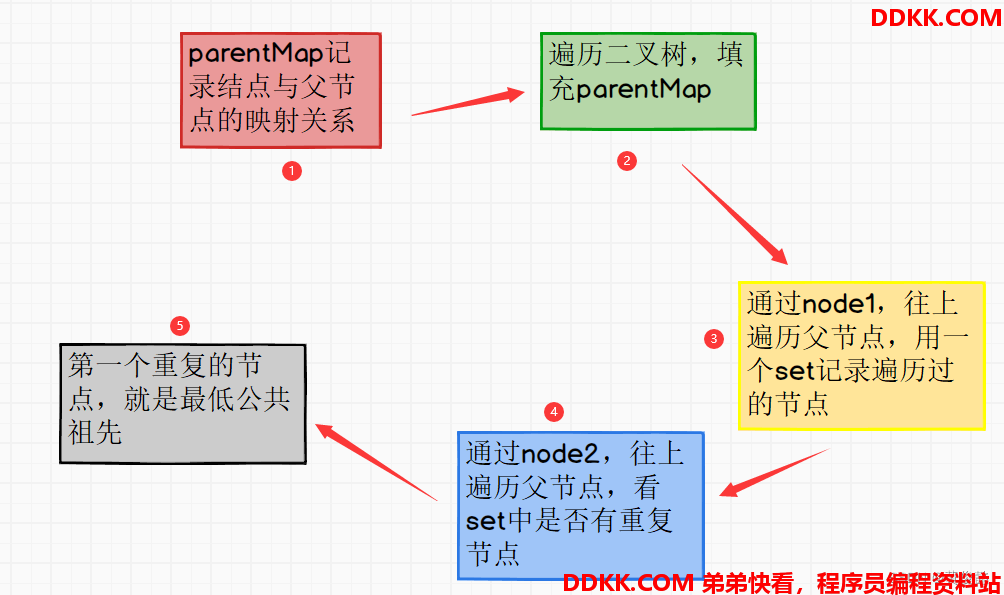
二叉树中寻找两个结点的最低公共祖先
/**
* 二叉树中寻找两个结点的最低公共祖先
*/
public class Tree08 {
public static Node findLowestAncestor(Node head, Node node1, Node node2) {
if (head == null) return null;
//parentMap记录结点与父节点的映射关系
Map<Node, Node> parentMap = new HashMap<>();
parentMap.put(head, null);
//填充parentMap
fillParentMap(head, parentMap);
Set<Node> node1Path = new HashSet<>();
//拿着node1结点通过parentMap往上遍历,记录走过的路径,记录到一个set中
Node curr = node1;
node1Path.add(curr);
while (parentMap.get(curr) != null) {
curr = parentMap.get(curr);
node1Path.add(curr);
}
//拿着node2结点通过parentMap往上遍历,遇到set中记录的结点,就是两结点的最低公共祖先
curr = node2;
while (!node1Path.contains(curr)) {
curr = parentMap.get(curr);
}
return curr;
}
private static void fillParentMap(Node node, Map<Node, Node> parentMap) {
if (node.left != null) {
parentMap.put(node.left, node);
fillParentMap(node.left, parentMap);
}
if (node.right != null) {
parentMap.put(node.right, node);
fillParentMap(node.right, parentMap);
}
}
private static class Node {
private int value;
private Node left;
private Node right;
}
}