堆结构
一种以数组模拟二叉树的结构
分大顶堆和小顶堆
如果是大顶堆,则父节点比两个孩子节点大,但是孩子节点间不做比较
小顶堆则是父节点比两个孩子节点小
以数组下标0位置作为根节点,1作为左孩子,2最为右孩子,后面的以此类推
则有下标换算公式:
left:2 * i + 1
rifht:2 * i + 2
parent:(i - 1) / 2
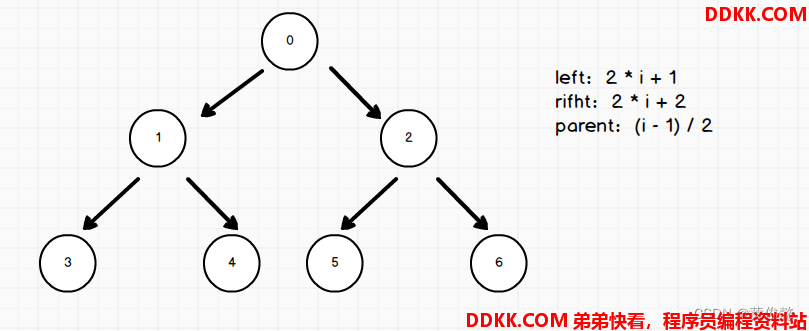
也可以以数组下标1作为根节点,则下标换算公式是:
left:2 * i
rifht:2 * i + 1
parent:i / 2
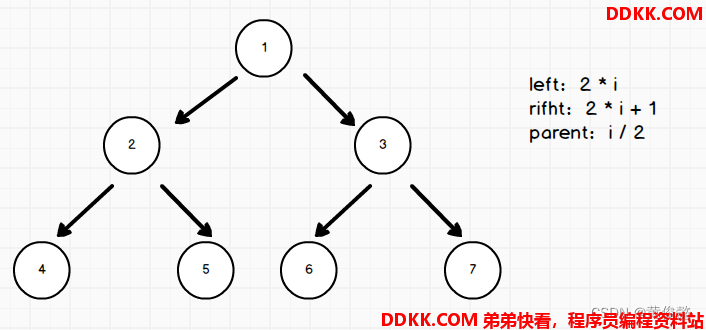
插入一个节点时,先插入到尾部(size位置),然后在size++,然后做向上调整
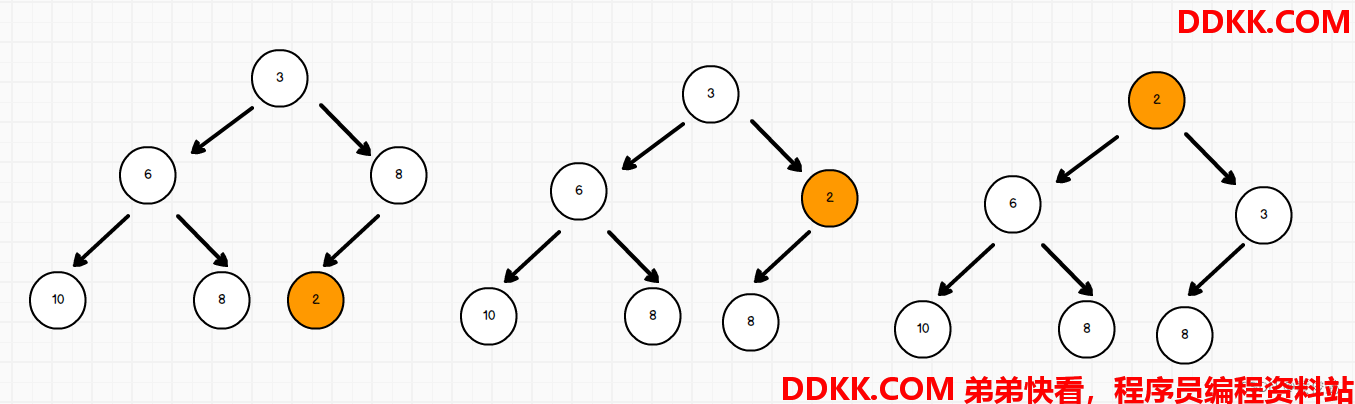
弹出一个节点时,先把头结点与尾部节点交换,然后size–,然后头结点做向下调整
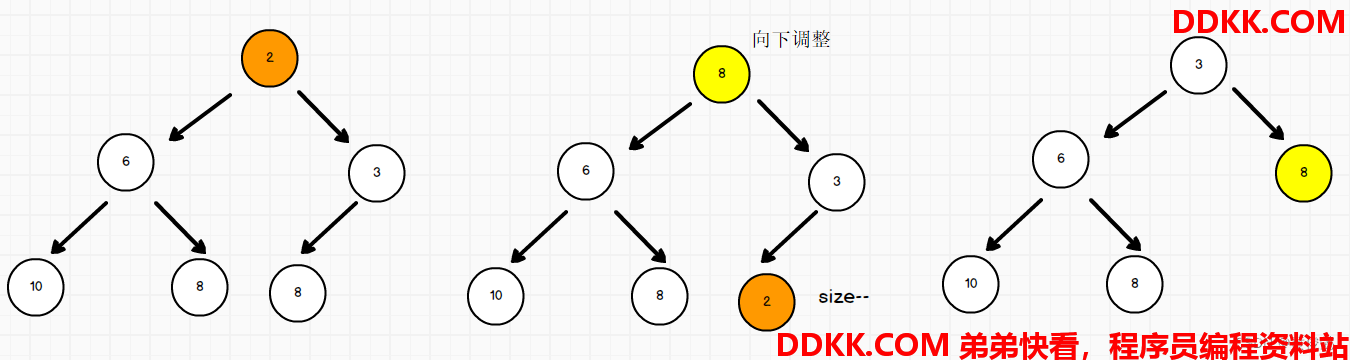
/**
* 堆结构(大根堆)
*/
public class Heap01 {
private int[] arr;
private int heapSize;
public Heap01(int size) {
arr = new int[size];
heapSize = 0;
}
public void push(int num) {
if (heapSize == arr.length) throw new RuntimeException("heap is full");
arr[heapSize] = num;
//堆调整:上浮
floatUp(arr, heapSize++);
}
private void floatUp(int[] arr, int index) {
//堆调整:上浮
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void sink(int[] arr, int heapSize) {
//堆调整:下沉
int index = 0;
int l = index * 2 + 1;
int r;
int bigSon;
//还有左孩子,就继续比较,没有左孩子,就不再比较了
while (l < heapSize) {
r = index * 2 + 2;
bigSon = r < heapSize && arr[r] > arr[l] ? r : l;
if (arr[bigSon] <= arr[index]) break;
swap(arr, index, bigSon);
index = bigSon;
l = index * 2 + 1;
}
}
public int pop() {
if (heapSize == 0) throw new RuntimeException("heap is empty");
int res = arr[0];
swap(arr, 0, --heapSize);
sink(arr, heapSize);
return res;
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
堆排序
1、 先遍数组,每个数做向上调整,相当于入堆,建立堆结构;
2、 然后每次把堆顶数与尾部数(size-1位置)交换,size–,换到尾部的数是最大的,不再动了;
3、 然后当前堆顶做向下调整,调整好后,继续堆顶与尾部数交换,依次类推;
/**
* 堆排序
*/
public class Heap02 {
public static void sort(int[] arr) {
if (arr == null || arr.length < 2) return;
//模拟从数组放入元素,调整为大顶堆
for (int i = 0; i < arr.length; i++) {
floatUp(arr, i);
}
int heapSize = arr.length;
while (true) {
swap(arr, 0, --heapSize);
if (heapSize == 0) break;
sink(arr, heapSize);
}
}
private static void floatUp(int[] arr, int index) {
//堆调整:上浮
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private static void sink(int[] arr, int heapSize) {
//堆调整:下沉
int index = 0;
int l = index * 2 + 1;
int r;
int bigSon;
//还有左孩子,就继续比较,没有左孩子,就不再比较了
while (l < heapSize) {
r = index * 2 + 2;
bigSon = r < heapSize && arr[r] > arr[l] ? r : l;
if (arr[bigSon] <= arr[index]) break;
swap(arr, index, bigSon);
index = bigSon;
l = index * 2 + 1;
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
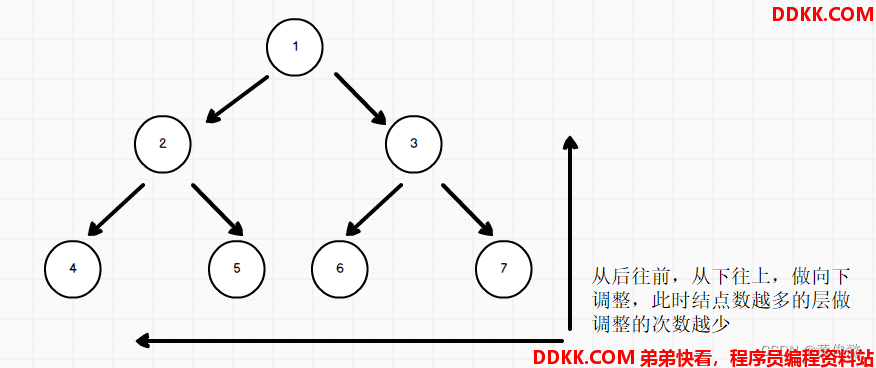
从上往下建堆复杂度是O(N * logN),建堆的过程可以优化,改为从下往上建堆,就是数组从后往前做向下调整,建堆的过程可以优化为O(N)
几乎有序的数组排序问题
一个数组几乎有序,数组在排序完之后,每一个数距离原位置移动的距离不超过k
给定一个数组,与k,对数组进行排序
先建一个k+1大小的小根堆,把前k+1个数入堆,然后弹出一个数放0位置,k+1位置的数入堆,再弹出一个数放1位置,一次类推,从堆弹出一个数放好,再把1一个数入堆,最后没数入堆了,就一次弹出直到弹空。时间复杂度O(N * logK)。
/**
* 几乎有序的数组排序问题:
* 一个数组几乎有序,数组在排序完之后,每一个数距离原位置移动的距离不超过k
* 给定一个数组,与k,对数组进行排序
*/
public class Heap03 {
public static void sort(int[] arr, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
int index = 0;
for (; index <= Math.min(arr.length - 1, k); index++) {
heap.add(arr[index]);
}
int i = 0;
for (; index < arr.length; index++) {
arr[i++] = heap.poll();
heap.add(arr[index]);
}
while (!heap.isEmpty()) {
arr[i++] = heap.poll();
}
}
}
线段最大重合问题
给定很多线段,每个线段都有两个数[start, end]
表示线段的开始位置和结束位置,左闭右闭区间
规定:
1)线段的开始位置和结束位置都是整数值
2)线段的重合区域必须>=1
返回线段最多重合区域中,包含了几条线段
1、 先把选的按开始位置从小打到排序;
2、 建立一个小根堆,由于存放线段的结束位置;
3、 遍历每一条线段,把堆中小于当前线段的结束位置弹出,然后把当前线段的结束位置放入堆中;
4、 结算堆中的线段数,与返回值pk一下,抓住最大值;
/**
* 线段最大重合问题
* 给定很多线段,每个线段都有两个数[start, end]
* 表示线段的开始位置和结束位置,左闭右闭区间
* 规定:
* 1)线段的开始位置和结束位置都是整数值
* 2)线段的重合区域必须>=1
* 返回线段最多重合区域中,包含了几条线段
* Created by huangjunyi on 2022/11/20.
*/
public class Heap04 {
private static class Line {
int start;
int end;
public Line(int start, int end) {
this.start = start;
this.end = end;
}
}
public static int maxCover(int[][] m) {
if (m == null || m.length < 0) return 0;
int N = m.length;
// 线段数组
Line[] lines = new Line[N];
for (int i = 0; i < m.length; i++) {
lines[i] = new Line(m[i][0], m[i][1]);
}
// 按线段的开始位置从小到大排序
Arrays.sort(lines, (line1, line2) -> line1.start - line2.start);
// 小根堆,存放线段的结束位置
PriorityQueue<Integer> heap = new PriorityQueue<>();
int res = 0;
for (int i = 0; i < lines.length; i++) {
Line line = lines[i];
// 把小于等于当前线段开始位置的结束位置弹出
while (!heap.isEmpty() && heap.peek() <= line.start) heap.poll();
heap.add(line.end);
// 抓住最大值
res = Math.max(res, heap.size());
}
return res;
}
}
可动态调整的堆
PriorityQueue不支持修改了堆中元素的值后,动态调整堆结构,如果要支持这种功能的堆,只能自己改写堆结构
1、 需要一个Map作为反向索引表,记录元素到堆中位置的映射;
2、 元素入堆、出堆,反向索引表要同步更新;
3、 堆中两元素交换位置,反向索引表也要同步更新(可以封装到swap方法中);
4、 定一个方法,用于接收外部通知堆中某个元素已经被修改了,要做堆调整;
/**
* 可动态调整的堆:
* 当堆中的元素的值发生变化时,可以重新调整该元素在堆中的位置
*/
public class Heap05<T> {
private List<T> arr; // 堆容器
private Map<T, Integer> indexMap; // 反向索引表
private int heapSize; // 堆大小
private Comparator<T> comparator; // 比较器
public Heap05(Comparator<T> comparator) {
this.comparator = comparator;
this.arr = new ArrayList<>();
indexMap = new HashMap<>();
this.heapSize = 0;
}
public void push(T t) {
int size = arr.size();
arr.add(t); // 添加到尾部
indexMap.put(t, size); // 记录反向索引
floatUp(size); // 向上调整
heapSize++;
}
public T pop() {
T res = arr.get(0); // 弹出的元素
swap(0, heapSize - 1); // 与尾部交换
arr.remove(heapSize - 1); // 删掉要弹出的元素
indexMap.remove(res); // 删除反向索引
sink(0, --heapSize); // 交换到头部的元素,做向下调整
return res;
}
public void remove(T obj) {
T replace = arr.get(heapSize - 1); // 尾部元素
Integer index = indexMap.get(obj); // 要删除元素的位置
indexMap.remove(obj);
heapSize--;
if (obj == replace) return; // 如果要删除的元素,就是尾部元素,删除就走
arr.set(index, replace); // 尾部元素替换到删除位置
indexMap.put(replace, index); // 更新反向索引
resign(replace); // 堆调整
}
public void resign(T t) {
//元素的值发生变化,重新调整该元素在堆中的位置
int index = indexMap.get(t);
floatUp(index);
sink(index, heapSize);
}
public List<T> getALL() {
return new ArrayList<>(this.arr);
}
public boolean contains(T t) {
return indexMap.containsKey(t);
}
public int size() {
return heapSize;
}
public T peek() {
return arr.get(0);
}
private void floatUp(int index) {
//堆调整:上浮
//while (arr[index] > arr[(index - 1) / 2]) {
while (comparator.compare(arr.get(index), arr.get((index - 1) / 2)) > 0) {
swap(index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void sink(int index, int heapSize) {
//堆调整:下沉
int l = index * 2 + 1;
int r;
int bigSon;
//还有左孩子,就继续比较,没有左孩子,就不再比较了
while (l < heapSize) {
r = index * 2 + 2;
//bigSon = r < heapSize && arr[r] > arr[l] ? r : l;
bigSon = r < heapSize && comparator.compare(arr.get(r), arr.get(l)) > 0 ? r : l;
//if (arr[bigSon] <= arr[index]) break;
if (comparator.compare(arr.get(bigSon), arr.get(index)) <= 0) break;
swap(index, bigSon);
index = bigSon;
l = index * 2 + 1;
}
}
private void swap(int i, int j) {
//元素位置互换
T t1 = arr.get(i);
T t2 = arr.get(j);
arr.set(i, t2);
arr.set(j, t1);
//元素位置互换后,更新元素位置表
indexMap.put(t1, j);
indexMap.put(t2, i);
}
}
TopK中奖者问题
给定一个整形数组,int[] arr; 和一个布尔类型数组,boolean[] op
两个数组一定等长,假设长度为N,arr[i]表示客户编号,op[i]表示客户操作
arr= [3,3,1,2,1,2,5…
op= [T,T,T,T,F,T,F…
依次表示:3用户购买了一件商品,3用户购买了1件商品,1用户购买了1件商品,2用户购买了1件商品
1用户退货了1件商品,2用户购买了1件商品,5用户退货了1件商品
一对arr[i]和op就代表一个事件:
用户号位arr[i],op[i] == T就代表这个用户购买了一件商品
op[i] == F就代表这个用户退货了一件商品
现在你作为电商平台负责人,你想在每一个事件到来的时候,
都给购买次数最多的前K名用户颁奖。
所以每个事件发生后,你都需要一个得奖名单(得奖区)
得奖系统的规则:
1、 如果某个用户购买商品数位0,但是有发生了退货事件,则任务该事件无效,得奖名单和之前事件时一直,比如例子中的5用户;
2、 某用户发生购买商品事件,购买商品数+1,发生退货事件,购买商品数-1;
3、 每次都是最多K个用户得奖,K也是作为参数传入,如果根据全部规则,得奖人数确实不够K个,那就以不够的情况输出结果;
4、 得奖系统分为得奖区和候选区,任何用户只要购买数>0,一定在这两个区域中的一个;
5、 购买数最大的前K名用户进入得奖区,在最初时入股得奖区没有到达K个用户,那么新进来的用户直接进入得奖区;
6、 如果购买数不足以进入得奖区的用户,进入候选区;
7、 如果候选区购买最多的用户,已经足以进入得奖区,该用户就会替换得奖区中购买数最少的用户(大于才能替换),如果得奖区中购买数最少的用户有多个,就替换最早进入得奖区的用户,如果候选区中购买数最多的用户有多个,机会会给最早进入候选区的用户;
8、 候选区和得奖区是两套时间,因用户只会在其中一个区域,所以只会有一个区域的时间,另一个没有从得奖区出来进入候选区的用户,得奖区时间删除,进入候选区的时间就是当前事件的时间(可以理解为arr[i]和op[i]中的i),从候选区出来进入得奖区的用户,候选区时间删除,进入得奖区的时间就是当前事件的时间(可以理解为arr[i]和op[i]中的i);
9、 如果某个用户购买数==0,不管在哪个区域都离开,区域时间删除,离开是指彻底离开,哪个区域都不会找到该用户,如果下次该用户又发生购买行为,产生>)的购买数,会再次根据之前规则回到某个区域中,进入区域的时间重记;
请遍历arr数组和op数组,遍历每一步输出一个得奖名单
public List topK(int[] arr, boolean[] op, int k)
思路:
就是建立两个手写的堆,支持修改元素值后,动态调整
一个是候选者堆,按照购买数降序排序,购买数相同则按时间升序排序
一个是得奖者堆,按照购买数升序排序,购买数相同则按时间升序排序
然后遍历每一个事件,模拟事件发生,更新购买数,调整两个堆
候选者和得奖者交换,就是两个堆的堆顶PK一下,候选者堆顶PK赢了,就和得奖者堆顶交换
然后每一步遍历,都收一个得奖者堆的所有元素的id
/**
* 给定一个整形数组,int[] arr; 和一个布尔类型数组,boolean[] op
* 两个数组一定等长,假设长度为N,arr[i]表示客户编号,op[i]表示客户操作
* arr = [3,3,1,2,1,2,5...
* op = [T,T,T,T,F,T,F...
* 依次表示:3用户购买了一件商品,3用户购买了1件商品,1用户购买了1件商品,2用户购买了1件商品
* 1用户退货了1件商品,2用户购买了1件商品,5用户退货了1件商品
* 一对arr[i]和op就代表一个事件:
* 用户号位arr[i],op[i] == T就代表这个用户购买了一件商品
* op[i] == F就代表这个用户退货了一件商品
* 现在你作为电商平台负责人,你想在每一个事件到来的时候,
* 都给购买次数最多的前K名用户颁奖。
* 所以每个事件发生后,你都需要一个得奖名单(得奖区)
* 得奖系统的规则:
* 1、如果某个用户购买商品数位0,但是有发生了退货事件,则任务该事件无效,得奖名单和之前事件时一直,比如例子中的5用户
* 2、某用户发生购买商品事件,购买商品数+1,发生退货事件,购买商品数-1
* 3、每次都是最多K个用户得奖,K也是作为参数传入,如果根据全部规则,得奖人数确实不够K个,那就以不够的情况输出结果
* 4、得奖系统分为得奖区和候选区,任何用户只要购买数>0,一定在这两个区域中的一个
* 5、购买数最大的前K名用户进入得奖区,在最初时入股得奖区没有到达K个用户,那么新进来的用户直接进入得奖区
* 6、如果购买数不足以进入得奖区的用户,进入候选区
* 7、如果候选区购买最多的用户,已经足以进入得奖区,该用户就会替换得奖区中购买数最少的用户(大于才能替换),如果得奖区中购买数最少的用户有多个,就替换最早进入得奖区的用户,如果候选区中购买数最多的用户有多个,机会会给最早进入候选区的用户
* 8、候选区和得奖区是两套时间,因用户只会在其中一个区域,所以只会有一个区域的时间,另一个没有从得奖区出来进入候选区的用户,得奖区时间删除,进入候选区的时间就是当前事件的时间(可以理解为arr[i]和op[i]中的i),从候选区出来进入得奖区的用户,候选区时间删除,进入得奖区的时间就是当前事件的时间(可以理解为arr[i]和op[i]中的i)
* 9、如果某个用户购买数==0,不管在哪个区域都离开,区域时间删除,离开是指彻底离开,哪个区域都不会找到该用户,如果下次该用户又发生购买行为,产生>)的购买数,会再次根据之前规则回到某个区域中,进入区域的时间重记
* 请遍历arr数组和op数组,遍历每一步输出一个得奖名单
* public List<List<Integer>> topK(int[] arr, boolean[] op, int k)
* Created by huangjunyi on 2022/11/20.
*/
public class Heap06 {
private Map<Integer, Customer> customerMap; // id和用户的索引表
private Heap05<Customer> candidateHeap; // 候选者堆 大根堆 按购买数降序排,购买数相同按时间升序排
private Heap05<Customer> winnerHeap; // 得奖者堆 小跟堆 按购买数升序排,购买数相同按时间降序排
private int K; // 指定得奖的用户数
public List<List<Integer>> topK(int[] arr, boolean[] op, int k) {
this.K = k;
customerMap = new HashMap<>();
candidateHeap = new Heap05<>(((o1, o2) -> o1.buy != o2.buy ? o2.buy - o1.buy : o1.time - o2.time));
winnerHeap = new Heap05<>(((o1, o2) -> o1.buy != o2.buy ? o1.buy - o2.buy : o1.time - o2.time));
// 遍历所有事件 => 执行 => 获取得奖者名单
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
int id = arr[i];
boolean buy = op[i];
int time = i;
operate(id, buy, time);
res.add(getWinners());
}
return res;
}
/**
* 获取当前得奖者名单(id列表)
* @return
*/
private List<Integer> getWinners() {
// 直接取得奖者堆中所有元素的id
List<Customer> customers = winnerHeap.getALL();
return customers.stream().map(customer -> customer.id).collect(Collectors.toList());
}
/**
* 事件处理
* @param id 用户id
* @param buy 是否购买,购买 true,退货 false
* @param time 事件发生时间
*/
private void operate(int id, boolean buy, int time) {
// 规则1 如果某个用户购买商品数位0,但是有发生了退货事件,则任务该事件无效
if (!buy && !customerMap.containsKey(id)) return;
// 不存在该用户,先初始化
if (!customerMap.containsKey(id)) customerMap.put(id, new Customer(id, 0, 0));
// 更新用户购买数
Customer customer = customerMap.get(id);
if (buy) customer.buy++; else customer.buy--;
// 如果用户购买数位0,删除
if (customer.buy == 0) customerMap.remove(id);
// 更新候选者堆和得奖者堆
if (!candidateHeap.contains(customer) && !winnerHeap.contains(customer)) {
// 候选者堆和得奖者堆都没有该用户,代表是新用户
if (winnerHeap.size() < K) {
// 得奖者堆没满,直接进
customer.time = time;
winnerHeap.push(customer);
} else {
// 得奖者堆满了,先进入候选者堆
customer.time = time;
candidateHeap.push(customer);
}
} else if (candidateHeap.contains(customer)) {
// 候选者堆包含该用户,如果购买数为0,删掉,否者堆调整
if (customer.buy == 0) {
candidateHeap.remove(customer);
} else {
candidateHeap.resign(customer);
}
} else {
// 得奖者堆包含该用户,如果购买数为0,删掉,否者堆调整
if (customer.buy == 0) {
winnerHeap.remove(customer);
} else {
winnerHeap.resign(customer);
}
}
move(time);
}
private void move(int time) {
// 候选者堆空,返回
if (candidateHeap.size() == 0) return;
// 候选者堆不空,但是得奖者堆没满,那是前面删掉了一个得奖者
if (winnerHeap.size() < K) {
Customer pop = candidateHeap.pop();
pop.time = time;
winnerHeap.push(pop);
}
// 候选者堆不空,得奖者堆满了,如果候选者堆顶PK过了得奖者堆顶,交换
else {
if (candidateHeap.peek().buy > winnerHeap.peek().buy) {
Customer oldCandidate = candidateHeap.pop();
Customer oldWinner = winnerHeap.pop();
oldCandidate.time = time;
oldWinner.time = time;
winnerHeap.push(oldCandidate);
candidateHeap.push(oldWinner);
}
}
}
private class Customer {
int id;
int buy;
int time;
public Customer(int id, int buy, int time) {
this.id = id;
this.buy = buy;
this.time = time;
}
}
}