线段树的作用
以O(logN)的时间复杂度对数组区间进行增加、修改、查询
普通的数组操作是要O(N)复杂度的
原理就是把数组组织为一颗树,数的每个节点对应数组不同区间,增加、修改、查询在数的节点上进行
线段树实现细节
线段树中,数组0位置一般是不使用的
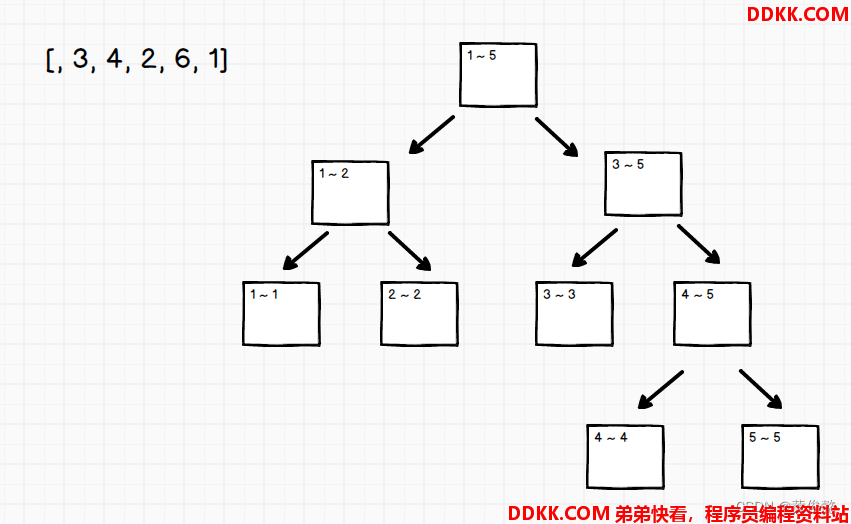
但是不会组织为真正的树状结构,而是组织为堆,下标从1开始,记为sum数组
下标0格子代表原数组1~5的累加和
下标1格子代表原数组1~2的累加和
…

如果此时要对某一范围进行增加操作 add(L, R, V)
要在组织一个跟sum数组一样长的lazy数组,表示懒更新信息
把该增加操作视为一个任务,范围为L~R
如果一个格子负责的范围被任务范围包住,就在lazy数组对应位置记录一个待增加值V
这个任务范围可能包住多个不同的格子,更新好lazy数组对应的所有位置就OK
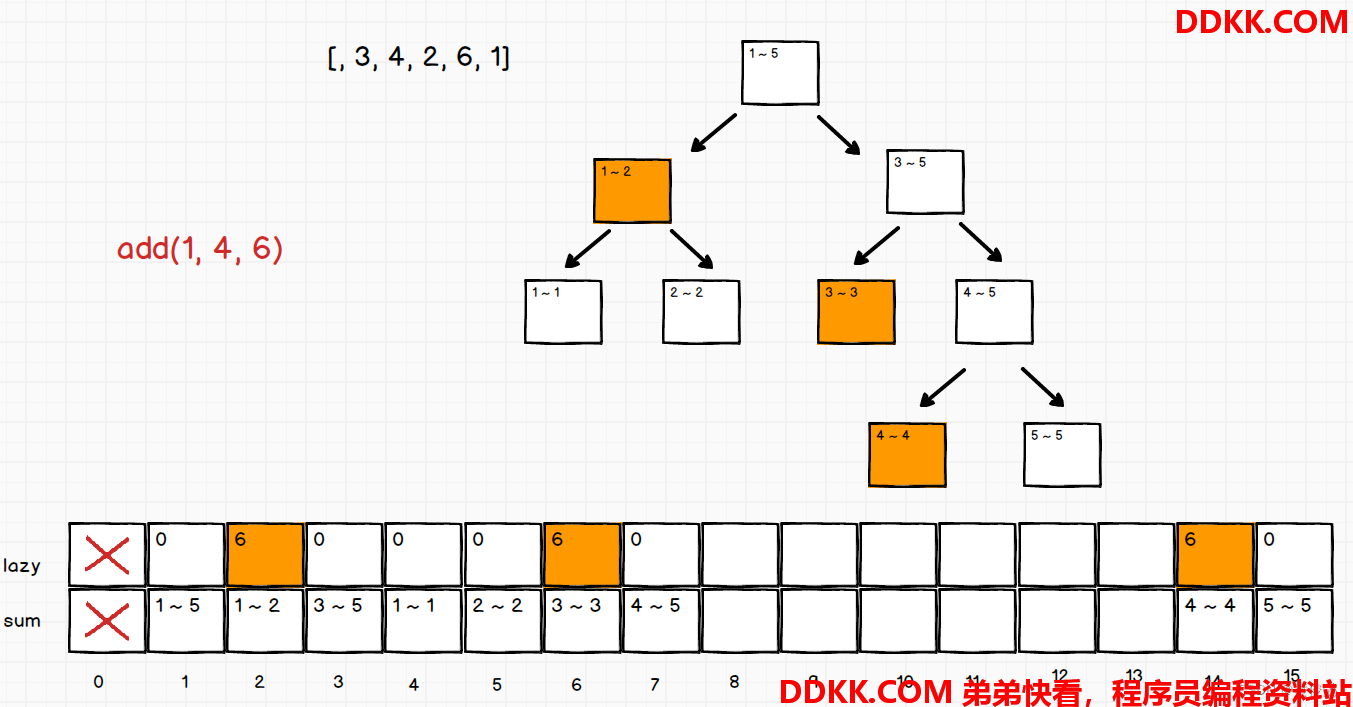
如果lazy数组对应位置原先就有任务hold住,那么把任务往下发一层
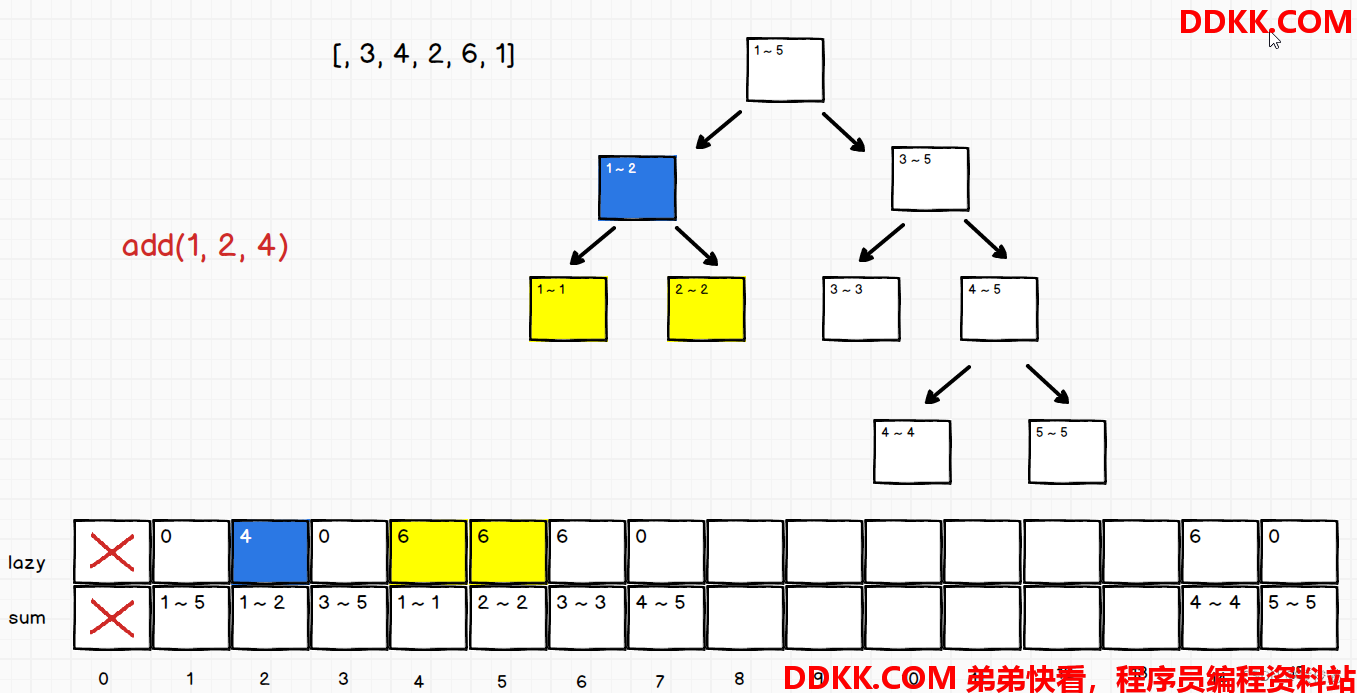
修改操作也是一样的,有一个和sum数组一样长的数组change,表示对应范围修改为什么值,update数组表示对应范围是否有修改任务(boolean类型),
要增加一个boolean类型的update数组,是因为如果change[i] = 0,那么区分不出是原来就是0(数组初始值就是0),还是更新为0,所以弄一个update数组,update[i] = true 表示是修改,update[i] = false,表示没有修改
线段树流程代码
/**
* 线段树,使得对数组范围更新、增加、查询的时间复杂度变成O(logn)
* Created by huangjunyi on 2022/9/10.
*/
public class SegmentTree01 {
private int lenght;
private int[] arr;
private int[] sum; // 范围累加和信息
private int[] lazy; // 范围懒增加信息
private int[] change; // 范围修改信息
private boolean[] update; // 范围修改标志
public SegmentTree01(int[] original) {
//arr为原数组长度加1,0下标弃而不用
int[] arr = new int[original.length + 1];
for (int i = 0; i < original.length; i++) {
arr[i + 1] = original[i];
}
lenght = original.length + 1;
// 4倍长度
sum = new int[lenght << 2];
lazy = new int[lenght << 2];
change = new int[lenght << 2];
update = new boolean[lenght << 2];
}
/**
* 构建,初始化sum数组
* @param l 原数组范围左边界
* @param r 原数组范围右边界
* @param rt 当前节点下标,从1开始
*/
public void build(int l, int r, int rt) {
if (l == r) {
// base case,来到叶子节点
sum[rt] = arr[l];
return;
}
int mid = (l + r) >> 1;
// 递归构建左子树
build(l, mid, rt << 1);
// 递归构建右子树
build(mid + 1, r, (rt << 1) | 1);
// 累加左右孩子的值
pushUp(rt);
}
/**
* add任务,指定范围的数都增加指定的值
* @param L 指定范围的左边界
* @param R 指定范围的右边界
* @param C 指定增加的值
* @param l 当前节点代表范围的左边界
* @param r 当前节点代表范围的右边界
* @param rt 当前节点下标
*/
public void add(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
// 任务把格子包住了,不用往下发了,更新sum数组和lazy数组中自己的信息
sum[rt] += (r - l + 1) * C;
lazy[rt] += C;
return;
}
// 任务没保住当前这个格子,要下发任务
int mid = (l + r) >> 1;
// 先把之前的任务往下发一层
pushDown(rt, mid - l + 1, r - mid);
// 任务需要发给左边
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
// 任务需要发给右边
if (R > mid) {
add(L, R, C, mid + 1, r, (rt << 1) | 1);
}
// 左右都调对了,抓住左右孩子的累加和,更新自己的累加和
pushUp(rt);
}
/**
* 更新任务,指定范围内的数都更新为指定的值
* @param L 指定范围的左边界
* @param R 指定范围的右边界
* @param C 指定范围更新的值
* @param l 当前节点代表范围的左边界
* @param r 当前节点代表范围的右边界
* @param rt 当前节点的下标
*/
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
// base case,任务范围把这个结点的范围包住了,不用下发任务了,更新chagne数组和update数组中自己的信息
change[rt] = C;
update[rt] = true;
// 更新要把之前攒的lazy失效调
lazy[rt] = 0;
// 调整sum
sum[rt] = C * (r - l + 1);
return;
}
// 没包住,先下发之前的任务
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, (rt << 1) | 1);
}
pushUp(rt);
}
/**
* 查询任务,查询指定范围内的数的总和
* @param L 指定范围的左边界
* @param R 指定范围的右边界
* @param l 当前节点代表范围的左边界
* @param r 当前节点代表范围的右边界
* @param rt 当前节点的下标
* @return
*/
public int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
// 任务范围把当前节点范围全包了,不有往下查了,直接返回
return sum[rt];
}
// 任务范围没有覆盖当前节点范围,需要往下查,但是查之前要把之前积攒的任务发下去
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - l);
// 任务发好了,再去左右两边查
int res = 0;
if (L <= mid) {
res += query(L, R, l, mid, rt << 1);
}
if (R > mid) {
res += query(L, R, mid + 1, r, (rt << 1) | 1);
}
return res;
}
/**
* 任务下发,把父节点积攒的懒更新和懒增加都下发到子节点
* @param rt 父节点下标
* @param ln 左节点的范围有几个数
* @param rn 右节点的范围有几个数
*/
private void pushDown(int rt, int ln, int rn) {
// 先检查是否有update,因为update是要失效掉lazy的,
// 如果自己既有update任务又有lazy任务,lazy肯定是后面到的
// 所以先下发update任务,再下发lazy任务,表示在修改之后的值上做累加
// 更新是要覆盖掉左右孩子的sum和lazy信息的
if (update[rt]) {
// 更新左右孩子的update和change信息
update[rt << 1] = true;
update[(rt << 1) | 1] = true;
change[rt << 1] = change[rt];
change[(rt << 1) | 1] = change[rt];
// 覆盖掉左右孩子的sum和lazy信息
sum[rt << 1] = change[rt << 1] * ln;
sum[(rt << 1) | 1] = change[(rt << 1) | 1] * rn;
lazy[rt << 1] = 0;
lazy[(rt << 1) | 1] = 0;
// 自己的update信息下发好了
update[rt] = false;
}
// lazy不等于0,表示之前懒住了任务
if (lazy[rt] != 0) {
// 下发父节点的懒增加到下一层,更新下一层的lazy数组和sum数组
lazy[rt << 1] = lazy[rt];
lazy[(rt << 1) | 1] = lazy[rt];
sum[rt << 1] = lazy[rt] * ln;
sum[(rt << 1) | 1] = lazy[rt] * rn;
// 当前父节点的lazy清空
lazy[rt] = 0;
}
}
/**
* 父节点往左右子节点收集sum
* @param rt 父节点下标
*/
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[(rt << 1) | 1];
}
}
线段树应用:掉落的方块
力扣第699题
https://leetcode.cn/problems/falling-squares/
在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i 个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
/**
* 线段树应用:掉落的方块
* https://leetcode.cn/problems/falling-squares/
*
* 在二维平面上的 x 轴上,放置着一些方块。
* 给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i 个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
* 每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
* 在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
* 返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
* Created by huangjunyi on 2022/9/11.
*/
public class SegmentTree02 {
private static class SegmentTree {
private int[] change;
private boolean[] update;
private int[] max; // 改写线段树,变成max数组,求范围最大值
public SegmentTree(int size) {
int n = size + 1;
change = new int[n << 2];
update = new boolean[n << 2];
max = new int[n << 2];
}
public void update(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
update[rt] = true;
change[rt] = C;
max[rt] = C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, C, mid + 1, r, (rt << 1) | 1);
}
pushUp(rt);
}
public int query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) return max[rt];
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
int max = Integer.MIN_VALUE;
if (L <= mid) {
max = Math.max(max, query(L, R, l, mid, rt << 1));
}
if (R > mid) {
max = Math.max(max, query(L, R, mid + 1, r, (rt << 1) | 1));
}
return max;
}
/**
* pushUp改写为求左右两边的最大值
* @param rt 当前节点下标
*/
private void pushUp(int rt) {
max[rt] = Math.max(max[rt << 1], max[(rt << 1) | 1]);
}
private void pushDown(int rt, int ln, int rn) {
if (update[rt]) {
max[rt << 1] = max[rt];
max[(rt << 1) | 1] = max[rt];
change[rt << 1] = change[rt];
change[(rt << 1) | 1] = change[rt];
update[rt << 1] = true;
update[(rt << 1) | 1] = true;
update[rt] = false;
}
}
}
private Map<Integer, Integer> index(int[][] positions) {
// 所有方块的左右边界,先排个序
Set<Integer> sortedSet = new TreeSet<>();
for (int i = 0; i < positions.length; i++) {
int[] position = positions[i];
sortedSet.add(position[0]);
// 防止边界重合,左闭右开
sortedSet.add(position[0] + position[1] - 1);
}
// 建立方块边界在数组中下标的映射
Map<Integer, Integer> indexMap = new HashMap<>();
int count = 1;
for (Integer index : sortedSet) {
indexMap.put(index, count++);
}
return indexMap;
}
// 入口方法,positions数组[i, j] 表示从i位置落下一个长度为j的方块
public List<Integer> fallingSquares(int[][] positions) {
//positions转换为indexMap,x轴下标 -> 数组下标
Map<Integer, Integer> indexMap = index(positions);
SegmentTree segmentTree = new SegmentTree(indexMap.size());
int max = Integer.MIN_VALUE;
List<Integer> res = new ArrayList<>();
for (int i = 0; i < positions.length; i++) {
int[] position = positions[i]; // 当前任务
int L = indexMap.get(position[0]); // 任务范围左边界对应的下标
int R = indexMap.get(position[0] + position[1] - 1); // 任务范围右边界对应的下标
// 查询在任务范围内的原高度,然后累加上当前任务(方块)要增加的高度
int height = segmentTree.query(L, R, 1, indexMap.size(), 1) + position[1];
// PK 最大高度
max = Math.max(height, max);
// 收集答案
res.add(max);
// 下发更新任务
segmentTree.update(L, R, height, 1, indexMap.size(), 1);
}
return res;
}
}
线段树适用范围
区间范围问题,并且不关心范围内的具体状况,比如区间更新,区间查询,只需要把左右两边子范围的信息收集回来简单加工,这类问题适用于线段树。
如果需要调研范围内具体状况的,比如某一范围内,出现次数最多的数,就不行,因为有可能有某个数在左边范围不是出现次数最多的数,在右边范围内也不是出现次数最多的数,但是在整体范围内有可能是出现次数最多的。